ESM法による仕事関数の高精度計算#

従来の周期境界条件を用いたDFT計算では、表面や界面等の2次元の系を厳密に取り扱うことが困難でした。そこで、 $Z$ 軸方向の周期境界条件を取り除き、2次元 ( $XY$ ) のスラブ系を厳密に記述する方法として考案されたのがEffective Screening Medium (ESM)法です。ESM法では、電場印加・溶媒のシミュレーションだけではなく、低い計算コストで高精度に仕事関数が計算できることも特徴です。ここでは、第一原理計算ソフトウェアAdvance/PHASEに導入されたESM法を用いた金属表面や2次元材料の仕事関数の解析事例を紹介します。

keywords: 第一原理計算、仕事関数、ESM法、金属表面、２次元材料

ESM法の理論背景#

先ず、ESM法 [1] における周期境界条件の除去方法について説明します。周期系のDFT計算において全エネルギーは、

$\small{E_{\text{tot}}[\rho_{e}] = T[\rho_{e}] + E_{XC}[\rho_{e}] + \frac{1}{2} \int \int d\mathbf{r}_{1} d\mathbf{r}_{2} \{ \rho_{e}(\mathbf{r}_{1}) + \rho_{I}(\mathbf{r}_{1}) \} G(\mathbf{r}_{1}, \mathbf{r}_{2}) \{ \rho_{e}(\mathbf{r}_{2}) + \rho_{I}(\mathbf{r}_{2}) \} \quad (1)}$

と表わされます。右辺の第一項は運動エネルギー ( $T$ )、第二項は交換相関エネルギー ( $E_{XC}$ )、第三項は古典クーロンエネルギー ( $E_{\text{Coul}}$ )です。また、 $\rho_{e}$ 、 $\rho_{I}$ 、および $G$ は、それぞれ電子の電荷密度、原子核の電荷密度、および古典クーロン相互作用に関するグリーン関数です。

周期スラブ計算では、 $T$ と $E_{XC}$ が局所的ですが、 $E_{\text{Coul}}$ は $1/r$ に比例する非局所的な物理量であるため、 $E_{\text{Coul}}$ にスラブ間の相互作用も含まれます。従って、スラブ系の周期境界条件を取り除き、単一のスラブのエネルギーを求めるためには、周期系の全エネルギーにおいて $E_{\text{Coul}}$ のみを修正すればよいのです。具体的には、グリーン関数の $Z$ 成分のみを実空間とするLaue表示を適用することで解決されます [2]。つまり、 $E_{\text{Coul}}$ を実空間 ( $Z$ 軸) にて積分する際に、積分範囲を単一のスラブ内に限定すればよいのです。(周期系の場合には積分は波数空間にて実施されるため、空間的な制約を課すことが出来ません。)

ESM法は、 $Z$ 軸方向（スラブ表面に垂直な方向）に対して、グリーン関数 ( $G$ ) を用いて任意の境界条件を設定できるという特長があります。これにより、電場を印加した状態や溶媒中のような、多様な環境のシミュレーションが可能になります。今回の仕事関数の解析では、その応用例として「真空／スラブ／真空」という境界条件を適用しました。

仕事関数の計算方法#

仕事関数は、真空準位とフェルミ準位の差として定義されます。真空準位は、物質表面から十分に離れた点での静電ポテンシャルであるため、その値を正確に決定するには十分な厚さの真空層が必要です。ESM法を用いると、表面に垂直な方向の周期性がなくなり、真空領域の静電ポテンシャルが物理的に正しく平坦になります。図1は、ESM法を用いて計算した、面内平均静電ポテンシャルの表面垂直方向（Z方向）への依存性を示したものです。真空領域のポテンシャルに傾きがないため、真空準位を曖昧さなく一意に決定できます。

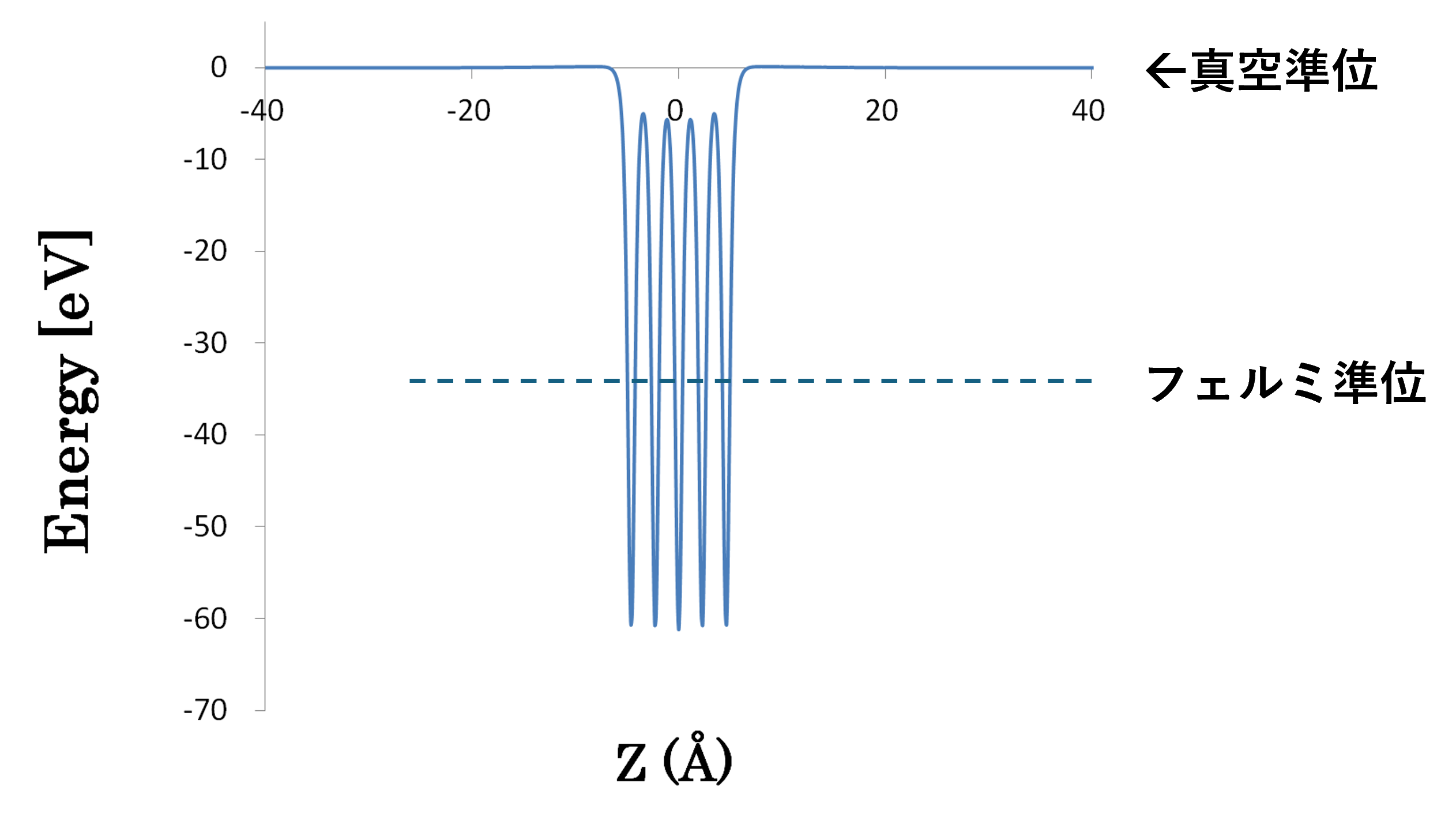
図1．ESM法で求めた静電ポテンシャルエネルギー（面内平均）の例

計算事例#

Cu(001)表面#

Cu(001)表面（図2）を対象に、仕事関数をESM法と従来の周期系計算で求め、実験値と比較しました。

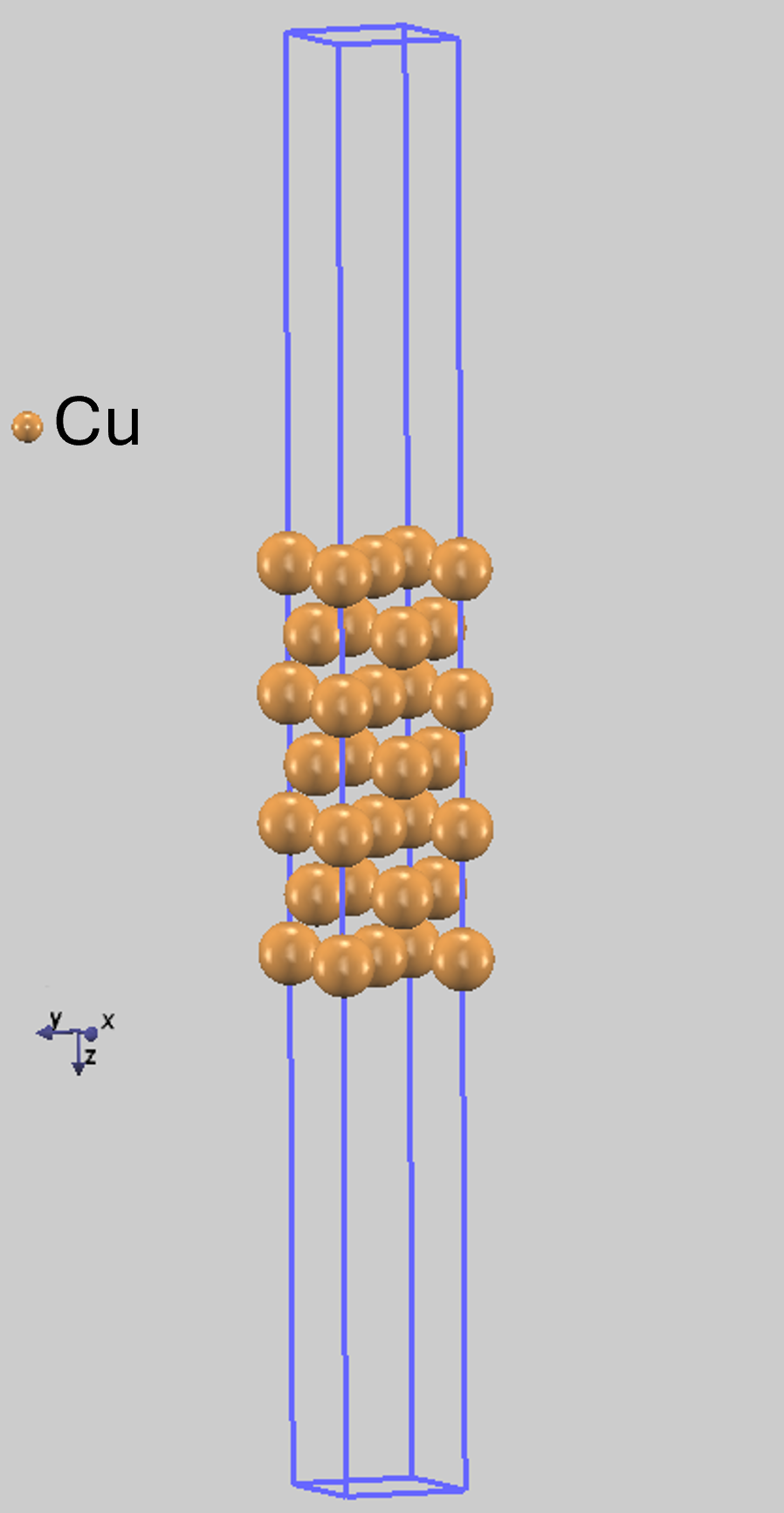
図2．Cu(001)表面の計算モデル

仕事関数

実験値 / eV	ESM法 / eV	周期系 / eV
4.65	4.60	4.10

計算時間 (Xeon 2.8 GHz, 6 core)

ESM法 / sec	周期系 / sec
240	727

ESM法による計算値は、実験値とよく一致しています。一方、30 Åの真空層を設けた周期系計算では、実験値との乖離が見られました。また、同一の計算機環境（Xeon 2.8 GHz, 6 core）で、仕事関数の計算に要した時間を比較しました。ESM法は周期系計算と比較して、計算時間が約1/3に短縮されました。これは、ESM法がカットオフエネルギーや真空層を小さく設定できるため、計算コストを大幅に削減できることを示しています。

単層グラフェン#

2次元材料の代表例として、単層グラフェン（図3）の計算結果を示します。ESM法による計算方法および従来の周期系計算方法を適用し、両者の結果を比較してESM法の優位性を確認します。

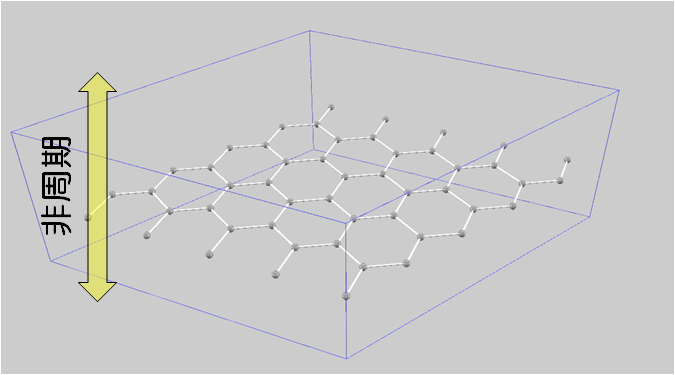
図3．単層グラフェン。ESM法を適用して、グラフェンの面に垂直な方向を非周期とします。

先ず、ユニットセル内の真空層の厚さを種々の値として、仕事関数を計算します。計算結果を表1に示します。計算に用いた波動関数および電荷密度のカットオフは、それぞれ36 Ryおよび400 Ryです。ESM法は非周期境界条件を課しているため、計算結果は真空層の厚さに無依存です。一方、周期系を用いた方法は真空層の厚さに依存しており、高精度な計算には十分な厚さの真空層が必要です。

表1．仕事関数の真空層厚さ依存性。

真空層の厚さ/Å	ESM法による仕事関数/eV	周期系計算方法による仕事関数/eV
10	4.24	4.00
14	4.24	4.03
18	4.24	4.05
22	4.24	4.06
26	4.24	4.07
30	4.24	4.08

次に、波動関数および電荷密度のカットオフエネルギーに対する依存性を確認します。種々のカットオフエネルギーにて計算された仕事関数の値を、表2に記します。計算に用いた真空層の厚さは 30 Å です。ESM法はカットオフエネルギーにほぼ無依存であり、Laue表示によってポテンシャルが高精度に記述できていることが示唆されます。周期系計算による方法では、仕事関数のカットオフエネルギー依存性が大きく、高精度な計算には十分大きなカットオフエネルギーが必要です。

表2．仕事関数のカットオフエネルギー依存性。

波動関数カットオフ/Ry	電荷密度カットオフ/Ry	ESM法による仕事関数/eV	周期系計算方法による仕事関数/eV
25	225	4.23	4.07
36	400	4.24	4.08
49	625	4.24	4.13
64	900	4.24	4.19

このように、ESM法を用いると、薄い真空層と小さいカットオフエネルギーにより低い計算コストで高精度に仕事関数が計算可能です。

まとめ#

Advance/PHASEに実装されたESM法を用いて、金属表面や2次元材料の仕事関数を計算しました。 Cu(001)表面の計算において、ESM法の結果(4.60 eV)が実験値(4.65 eV)と極めてよく一致したこと、また従来の周期系計算に比べて計算時間が約3分の1に短縮されたことが示されました。さらに、単層グラフェンの計算では、従来の周期系計算とは対照的に、ESM法の結果が真空層の厚さやカットオフエネルギーにほとんど依存しないことも実証されました。これらの結果は、ESM法が多様な表面系において、低い計算コストで信頼性の高い仕事関数を算出できる優れた手法であることを示しています。

参考文献#

M. Otani and O. Sugino, Phys. Rev. B 73, 115407 (2006)
I. Hamada, M. Otani, O. Sugino and Y. Morikawa, Phys. Rev. B 80, 165411 (2009).