鉄の水素脆化の第一原理シミュレーション：水素溶解エネルギーの解析#

PHASE logo

鉄鋼材料の強度を著しく低下させる水素脆化は、産業界における重要な課題です。この現象の根本的なメカニズムを理解するためには、鉄の結晶格子内に侵入した水素原子が、材料の結合状態にどのような影響を及ぼすかを原子・電子レベルで解明する必要があります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、体心立方格子(BCC)鉄中の格子間サイトに固溶した水素の溶解エネルギーを算出しました。このエネルギーは、水素が結晶中のどこに集まりやすいか、そして、なぜ特定の場所で材料の結合を弱めるのか（デコヒージョン）を理解するための基本的な物理量です。

Keywords: 第一原理計算, 水素脆化, 水素溶解エネルギー, 鉄, 零点振動エネルギー(ZPE), デコヒージョン

計算モデルと計算条件#

計算モデルとして、BCC鉄の3x3x3スーパーセル（54原子）を用いました。水素原子が1つだけ固溶する低濃度状態を想定し、水素原子が鉄格子に与える局所的な緩和効果に焦点を当てるため、計算コストと物理的妥当性のバランスを考慮し、セルの格子定数は固定しました。最適化したBCC鉄（2原子）の格子定数は2.844 Åです。

水素原子の侵入位置は、結晶格子の「隙間」を幾何学的に特定するPymatgen（同梱）のVoronoiInterstitialGeneratorを用いて決定しました [1]。この手法により、BCC鉄で格子間サイトとして最も安定とされる四面体サイト(t-site)を候補位置として特定しました。もう一つの候補サイトは八面体サイトとして知られていますが、エネルギー的に高いことは第一原理計算で確認されているため、本解析では対象外としました。

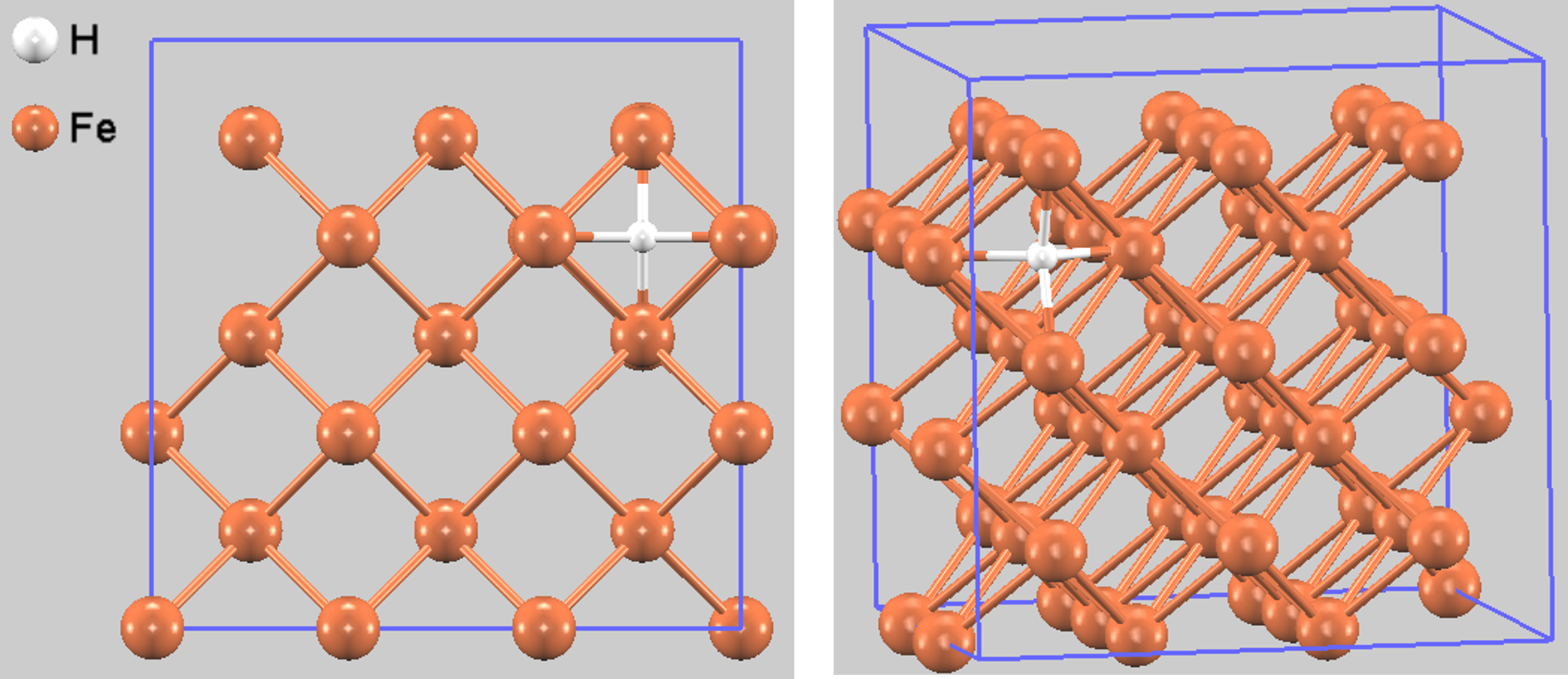
Optimized structure of H in bcc Fe

図1.　最適化されたBCC鉄中の水素原子の配置（側面図と斜視図）。白球が水素(H)、茶色の球が鉄(Fe)原子を示します。

本解析で用いた主な計算条件は表1に示されています。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	PAWポテンシャル
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Rydberg (約340 eV)
k点サンプリング (SCF計算)	4x4x4 (3x3x3スーパーセル)
スピン分極	あり (Feの初期スピン分極率: 0.275)

計算結果と考察#

構造最適化、差電荷密度と零点振動エネルギー#

構造最適化の結果、水素原子が四面体サイトに位置する安定構造（図1）が得られました。このときのFe-H原子間距離は1.663 Åでした。

図2は、水素原子の固溶によって電子がどのように再配置されるかを示した電荷密度差分布図です。水素原子の周囲に電荷密度が増加（赤色）する一方、近傍の鉄原子の周辺では電荷密度が減少（緑色）する傾向が見られます。これは、水素の存在がFe-Fe原子間の結合電子分布に影響を及ぼし、結合を弱めている可能性を示唆しています。

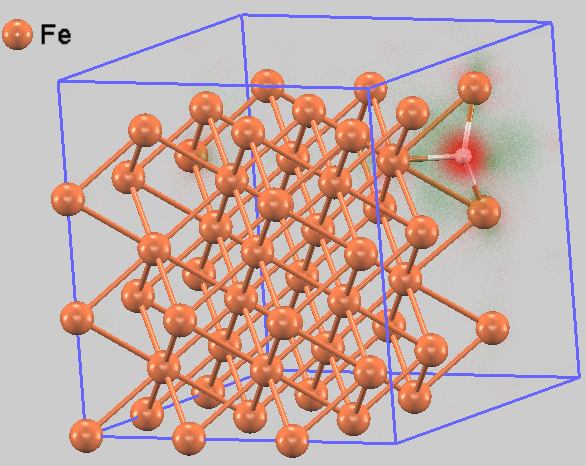
charge density difference distribution

図2.　水素原子周辺の電荷密度差分布図。赤色は電荷が増加した領域、緑色は減少した領域を示します。

水素のように軽い原子のエネルギーを精密に評価する際には、絶対零度でも原子が静止せずに振動している効果、すなわち零点振動エネルギー(ZPE)を考慮することが極めて重要です。ZPEは、各振動モードのエネルギーの和として計算されます。

$E_{\text{ZPE}} = \sum_{i=1}^{N} \frac{1}{2} h \nu_i$

ここで、 $N$ は基準振動の数、 $h$ はプランク定数、 $\nu_i$ は各振動モードの振動数です。この式は、量子力学において調和振動子のエネルギーがとびとびの値しかとれず、その最低エネルギーが0ではないこと（ $E_0 = \frac{1}{2}h\nu$ ）に由来します。系のZPEは、存在する全ての振動モードの最低エネルギーを足し合わせることで求められます。

BCC鉄中の水素の振動解析#

BCC鉄格子に束縛された水素原子は、並進や回転の自由度を持たず、3つの振動モードのみを持ちます。鉄原子は水素原子に比べて圧倒的に質量が大きいため、鉄原子の座標を固定し、水素原子のみを振動させることで計算を大幅に高速化しました。Advance/PHASEでは、図3のGUI設定のように、振動計算を行う原子の範囲を指定して、力計算を行ってから振動モードの解析が可能です。

GUI for specifying force calculation range in Advance/PHASE

図3.　Advance/PHASEにおける振動計算対象原子の指定GUI。

計算された振動周波数とZPEを表2に示します。

表2.　BCC鉄中の水素原子の振動周波数と零点エネルギー(ZPE)

振動モード	周波数 (cm^-1)
モード 1	968
モード 2	1450
モード 3	1450
合計ZPE	0.240 eV

この結果は、2つの縮退した高周波モードと1つの低周波モードが存在することを示しており、先行研究 [2] のフォノン分散計算の結果（約29.6 THzに単一モード、約43.7 THzに二重縮退モード）ともよく一致しています。

気相H₂分子の振動解析#

溶解エネルギーの基準となる気相の水素分子（H₂）についても、同様に振動解析を行いました。10 Åのボックスサイズで計算した結果、振動周波数は 4073 cm^-1 となり、これは文献値 (GGA-PBE) の 4077 cm^-1 と非常によい一致を示しました [3]。この周波数から計算されるH₂分子一個あたりのZPEは 0.253 eV です。

水素溶解エネルギーの算出#

水素溶解エネルギー( $\Delta E$ )は、水素原子を含む鉄( $E_{\text{Fe54}\text{H}}$ )の全エネルギー、純粋な鉄( $E_{\text{Fe54}}$ )の全エネルギー、および気相中の水素分子( $E_{\text{H2}}$ )の全エネルギーを用いて、以下の式で算出されます。この際、ZPEの寄与( $\Delta E_{\text{ZPE}}$ )も補正項として加えます。

$\Delta E = E_{\text{Fe54}\text{H}} - E_{\text{Fe54}} - \frac{1}{2} E_{\text{H2}} + \Delta E_{\text{ZPE}}$

$\Delta E_{\text{ZPE}}$ は、固溶した水素のZPEと、基準となるH₂分子のZPEの半分との差であり、以下のように計算されます。

$\Delta E_{\text{ZPE}} = E_{\text{ZPE}}(\text{H in Fe}_{54}) - \frac{1}{2} E_{\text{ZPE}}(\text{H}_2)$

最終的に得られた水素溶解エネルギーと実験値 [4] を表3にまとめます。

表3.　水素溶解エネルギー: 本計算と実験値の比較

項目	エネルギー (eV)
本計算値 ( $\Delta E$ )	0.26
実験値 [4]	0.29

本計算で得られた溶解エネルギー 0.26 eV は、実験値 0.29 eV と良好な一致を示しました。

考察#

溶解エネルギーが+0.26 eVという正の値であることは、水素原子が完全な鉄の結晶格子内部に存在することがエネルギー的に不安定であることを示しています。この不安定性こそが、水素をより安定な場所、すなわち結晶粒界、転位、き裂先端といったエネルギーの高い「欠陥」部分へと集積させる駆動力となります。欠陥部に高濃度で集まった水素は、周囲の鉄原子間の結合を著しく弱め（局所的なデコヒージョン）、材料が本来持つ強度よりもはるかに小さな力で破壊に至らせます。したがって、本計算で得られた正の溶解エネルギーは、水素が材料の弱点へと移動し、そこから破壊を引き起こすという水素脆化の根本的なメカニズムを裏付けるものです。

本解析で得られた基礎的な知見は、より複雑な現象の解明へと繋がります。例えば、水素原子における原子空孔へのトラップとそれに続く異方的な空孔クラスターの形成 [5]、水素の拡散ダイナミクス（活性化エネルギーの計算）[6]、など、第一原理計算を用いた発展的な研究が報告されています。これらの研究は、原子スケールの挙動と巨視的な破壊現象を繋ぎ、水素脆化の全体像を理解する上で不可欠です。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、BCC鉄における水素溶解エネルギーを高精度に算出しました。零点振動エネルギー(ZPE)を考慮した結果、溶解エネルギーは0.26 eVとなり、実験値とよく一致しました。この結果は、水素が鉄の完全な結晶格子中では不安定であり、結晶欠陥部に集積する傾向があることを定量的に示しています。これは、水素脆化がき裂先端などの応力集中部で優先的に発生するメカニズム（デコヒージョン）の駆動力を説明するものであり、第一原理計算が材料の破壊現象を原子・電子レベルで解明する上で強力なツールであることを示しています。

参考文献#

S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. Chevrier, K. A. Persson, and G. Ceder, "Python Materials Genomics (pymatgen) : A Robust, Open-Source Python Library for Materials Analysis", Comp. Mater. Sci. 68, 314 (2013).
K. Hirata, S. Iikubo, M. Koyama, K. Tsuzaki, and H. Ohtani, "First-principles study on hydrogen diffusivity in BCC, FCC, and HCP iron", Metall. Mater. Trans. A 49, 5015 (2018).
Y. Okamoto, M. Saito, and A. Oshiyama, "Comparative study of vibrational frequencies of H2 molecules in Si and GaAs", Phys. Rev. B 56, R10016 (1997).
J. R. G. Da Silva, and R. B. Mclellan, "The solubility of hydrogen in super-pure-iron single crystals", J. Less Common Metals 50, 1 (1976).
Y. Tateyama and T. Ohno, "Stability and clusterization of hydrogen-vacancy complexes in α-Fe: an ab initio study", Phys. Rev. B 67, 174105 (2003).
D. E. Jiang, and E. A. Carter, "Diffusion of interstitial hydrogen into and through bcc Fe from first principles", Phys. Rev. B 70, 064102 (2004).