機械特性の異方性:弾性定数の3D可視化#

単結晶材料の機械特性は、結晶の方向によって大きく異なる「異方性」を示します。この異方性の理解は、材料の性能を最大限に引き出す設計において極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて各種材料の弾性定数テンソルを算出し、ヤング率と剛性率の異方性を3Dで可視化しました。これにより、材料がどの方向に硬く、どの方向に変形しやすいかを直感的に把握できます。
Keywords: 第一原理計算, DFTシミュレーション, 弾性定数, 異方性, ヤング率, 剛性率, 3D可視化, Si, W, Cs, SiC
計算モデルと計算条件#
第一原理計算による弾性定数の算出では、結晶に微小なひずみを与え、その際の応力テンソルを計算することで弾性スティフネス定数テンソル (\(C_{ij}\)) を算出しました。解析対象として、異方性の特徴が比較しやすい4つの物質(Si, W, Cs, 4H-SiC)を選定しました。計算された弾性定数を表1に、主な計算条件を表2に示します。
表1. 計算された独立な弾性定数 (GPa)
| 物質 | 結晶系 | \(C_{11}\) | \(C_{12}\) | \(C_{13}\) | \(C_{33}\) | \(C_{44}\) |
|---|---|---|---|---|---|---|
| Si | 立方晶 | 152.8 | 54.6 | - | - | 102.0 |
| W | 立方晶 | 457.5 | 175.7 | - | - | 120.5 |
| Cs | 立方晶 | 1.9 | 1.7 | - | - | 2.0 |
| 4H-SiC | 六方晶 | 496.2 | 71.7 | 29.9 | 527.9 | 164.7 |
表2. 主な計算条件
| 項目 | Si | W | Cs | SiC |
|---|---|---|---|---|
| 擬ポテンシャル | PAW | PAW | PAW | PAW |
| 交換相関汎関数 | GGA-PBE | GGA-PBE | GGA-PBE | GGA-PBE |
| カットオフエネルギー (Ry) | 16 | 25 | 36 | 25 |
| k点サンプリング | 10x10x10 | 10x10x10 | 10x10x10 | 8x8x2 |
可視化結果と考察#
算出された弾性定数は、PythonツールであるELATE [1, 2] を用いて3D可視化しました。
代表例: シリコン (Si) の弾性異方性#
立方晶系の代表としてシリコン(Si)のヤング率と剛性率をプロットしました(図1)。3Dプロットは、原点からの距離がその方向の弾性率の大きさを示します。
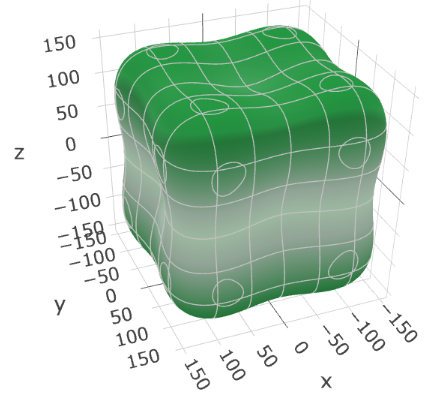
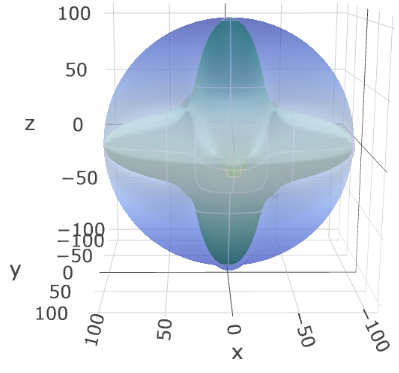
図1. シリコン(Si)のヤング率(左)と剛性率(右)の3Dプロット。原点からの距離がその方向の弾性率(単位: GPa)の大きさを示します。
ヤング率(図1左): プロットは完全な球ではなく、立方体の頂点方向(<111>方向)に最も膨らみ、座標軸方向(<100>方向)に窪んだ形状です。これはSi結晶が<111>方向に最も硬く、<100>方向に最も柔らかいことを示しています。Siの実験値 [3] では、最も硬い<111>方向が約188 GPa、最も柔らかい<100>方向が約130 GPaであり、本計算結果(図1左)も同様の異方性を示します。 この特徴的な形状は、立方晶のヤング率が結晶方位に依存するという物理法則を反映したものです。具体的には、<100>方向は主に \(C_{11}\) で、<111>方向は \(C_{11}\), \(C_{12}\), \(C_{44}\) の組み合わせで決まります。
剛性率(図1右): 剛性率のプロットは、各方向における最大値(青色半透明)と最小値(内側の緑色)を同時に示します。Siが特定の結晶面・方向に沿ってすべり変形しやすい、顕著な異方性を持つことがわかります。 剛性率は、力を加える方向だけでなく、どの結晶面で滑るかにも依存するため、一つの方向に対してこのように最大値と最小値が存在します。
異方性の比較: タングステン (W) vs セシウム (Cs)#
次に、異方性の大小を比較するため、タングステン(W)とセシウム(Cs)のヤング率を並べて示します(図2)。
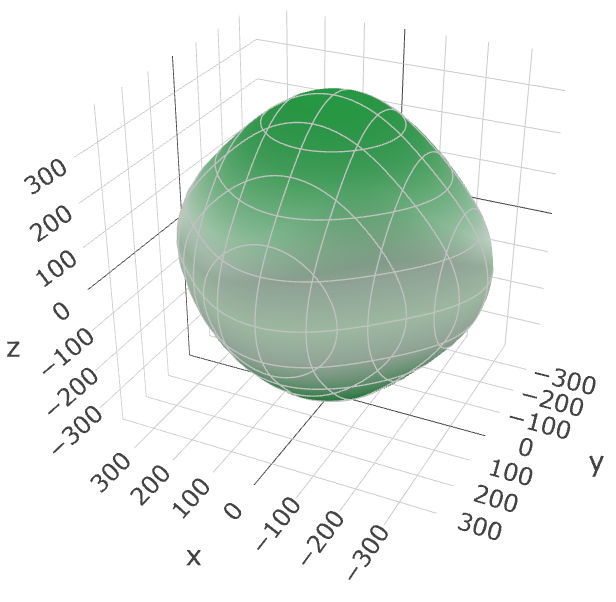
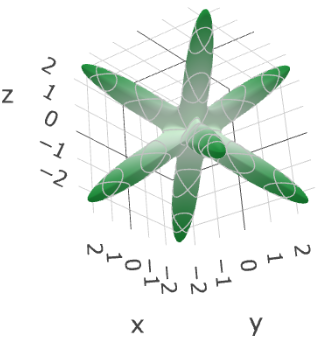
図2. タングステン(W)とセシウム(Cs)のヤング率3Dプロット比較。
タングステン(W): 3Dプロットはほぼ完全な球形に近く、どの方向に力を加えてもヤング率がほとんど変わらない、等方性が高い材料であることがわかります。
セシウム(Cs): プロットは星形のように大きく歪んだ形状です。特定の方向には硬い一方で、別の方向には極端に柔らかいという、非常に強い異方性を明確に示しています。
この異方性の度合いは、ゼナー比 \(A = 2C_{44}/(C_{11}−C_{12})\) という指標で定量化できます。A=1が完全な等方性を示し、今回の計算結果はタングステン(W)がA≈0.85と1に近いのに対し、セシウム(Cs)はA=20と1から大きく外れており、両者の違いが数値的にも裏付けられました。
六方晶の例: 炭化ケイ素 (SiC) の弾性異方性#
最後に、結晶構造が異なる例として、六方晶系の炭化ケイ素(SiC)をプロットします(図3)。
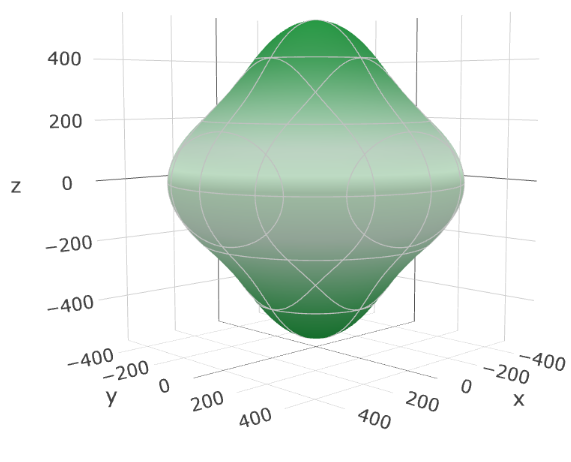
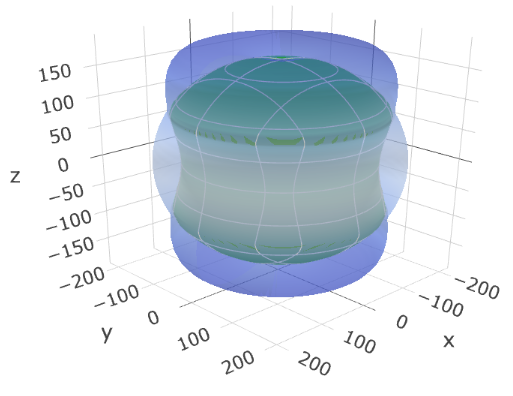
図3. 炭化ケイ素(SiC)のヤング率(左)と剛性率(右)の3Dプロット。
SiCのプロットはc軸(z軸)周りに回転対称な形状です。これは六方晶系の特徴を反映しており、基底面(a-b面)内とc軸方向で機械特性が異なることを示しています。表1のデータ (\(C_{11} \neq C_{33}\)) からも、c軸方向がより硬いことがわかります。このように、結晶の対称性が機械特性の異方性に直接反映されることが確認できます。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEで算出した弾性定数を用いて、各種材料の機械特性異方性を3D可視化しました。これにより、Siの一般的な異方性、WとCsにおける異方性の強弱、SiCの結晶構造と異方性の関係などを直感的に理解できることが示されました。本手法は、単結晶材料のデバイス設計や力学挙動の予測において、有用な知見を与えるものです。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- R. Gaillac, P. Pullumbi, and F. X. Coudert, "ELATE: an open-source online application for analysis and visualization of elastic tensors", J. Phys.: Condens. Matt. 28, 275201 (2016).
- https://github.com/coudertlab/elate
- J. J. Wortman, and R. A. Evans, "Young's modulus, shear modulus, and Poisson's ratio in silicon and germanium", J. Appl. Phys. 36, 153 (1965).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学