第一原理計算による弾性定数の予測と材料特性の探求#

材料の硬さや変形のしやすさといった機械的特性を支配する「弾性定数」は、新しい材料を設計・開発する上で最も基本的な物理量の一つです。第一原理計算は、実験を行うことなく材料の弾性定数を予測できる強力なツールですが、その計算精度は条件設定に敏感であり、常に信頼性が問われます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて多様な結晶の弾性定数を計算し、その信頼性を検証するとともに、得られたデータから材料の物理的特性を探求します。
Keywords: 第一原理計算, DFTシミュレーション, 弾性定数, ヤング率, 体積弾性率, せん断弾性率, ポアソン比
計算手法の概要#
弾性定数は、結晶に微小な「ひずみ」を与え、その応答として生じる「応力」を計算することで求められます。まず、ひずみのない状態で構造を最適化し、次に特定のひずみ(例:xx方向に0.01)を与えた上で応力テンソルを計算します。この応力とひずみの関係から、スティフネス定数 や、ヤング率・せん断弾性率などの各種弾性率が導出されます。また、E-V曲線から比較的精度のよい体積弾性率が算出されます。
計算精度:実験値との比較#
まず、金属から半導体まで、代表的な物質の体積弾性率について、GGA-PBEを用いたE-V曲線による計算値と信頼性の高い実験値 [1, 2] をプロットしたのが図1のパリティプロットです。データ点が対角線(y=x)に近いほど、計算が実験をよく再現していることを意味します。
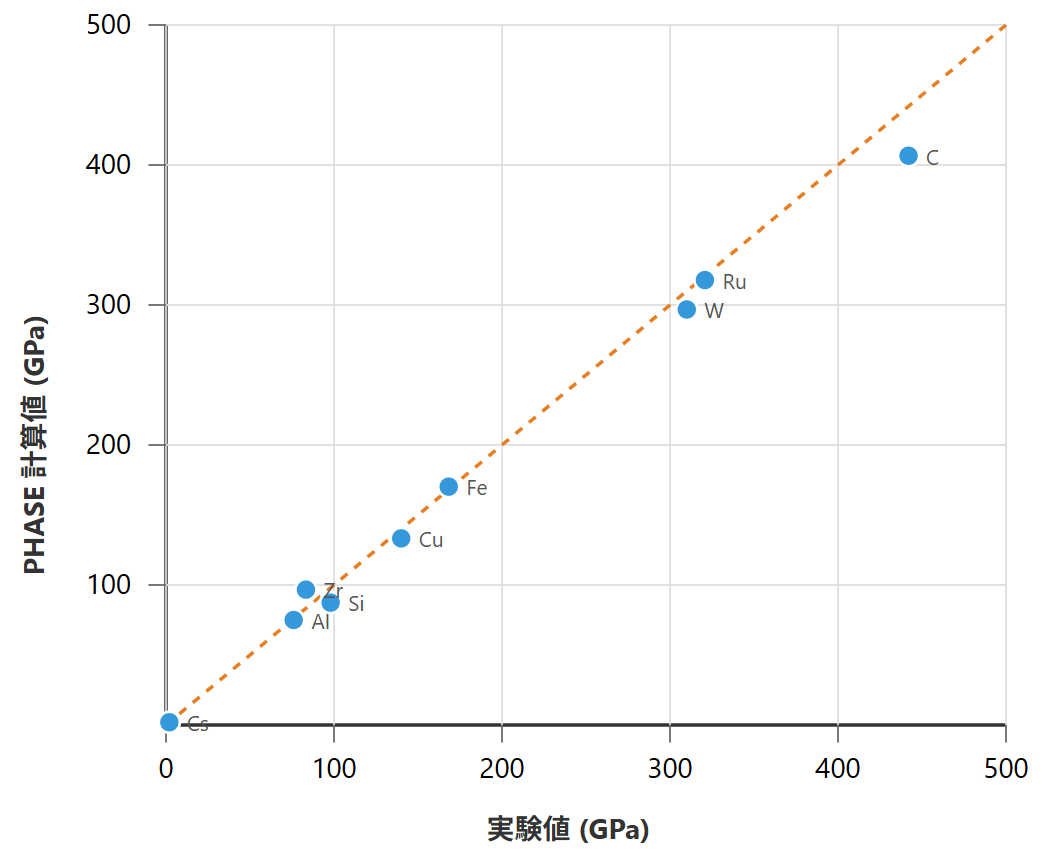
図1. 体積弾性率の計算値と実験値の比較
表1に示すように、一部のデータでは実験値との間に若干の乖離が見られるものの、全体としては良好な相関が得られています。これは、本計算手法が多様な材料に対して、弾性率を有効に予測できることを示唆しています。特にGGA汎関数を用いた場合、原子間の結合を実際よりもやや弱く評価する傾向があるため、体積弾性率が実験値よりやや小さく計算される傾向があり、その物理的な傾向も捉えられています。
表1. 体積弾性率の比較 (一部抜粋、単位: GPa)
| 物質 | PHASE 計算値 | 実験値 |
|---|---|---|
| Al | 75.0 | 76 |
| C (diamond) | 406.6 | 442 |
| Cs | 2.0 | 2 |
| Cu | 133.3 | 140 |
| Si | 87.4 | 98 |
| W | 296.8 | 310 |
テーマ別深掘り:データから探る材料の個性#
テーマ1:硬質材料の弾性率比較#
図1のプロットでは右上に位置する「硬い」材料は、工業的にも非常に重要です。ここでは特に硬いことで知られる物質の計算結果を抜き出し、その基本的な硬さの指標であるスティフネス定数を比較します(表2)。
表2. 代表的な硬質材料の計算されたスティフネス定数
| 物質 | 結晶構造 | 主要なスティフネス定数 (GPa) |
|---|---|---|
| C (ダイヤモンド) | 立方晶 | c11 = 951.6 |
| SiC (4Hポリタイプ) | 六方晶 | c11 = 496.2, c33 = 527.9 |
| Ru | 六方晶 | c11 = 545.5, c33 = 671.8 |
| W | 立方晶 | c11 = 457.5 |
表2から、ダイヤモンド(C)やルテニウム(Ru)のスティフネス定数が極めて高いことがわかります。ダイヤモンドや炭化ケイ素(SiC)の硬さは、原子間の短く強固な共有結合に由来します。一方で、タングステン(W)やルテニウム(Ru)のような遷移金属の硬さは、高密度のd電子による強い金属結合に起因します。このように、第一原理計算で得られるスティフネス定数は、材料の硬さの序列だけでなく、その物理的な起源を探る上でも強力な手がかりを与えてくれます。
テーマ2:材料の「伸びにくさ」を測る - ヤング率#
ヤング率(縦弾性係数、)は、材料を単一方向に引き伸ばしたり圧縮したりした際の「変形のしにくさ」を示す指標です。値が大きいほど、材料は剛性が高く、伸ばすのに大きな力が必要になります。これは一般的に「硬さ」や「剛性」として最も直感的に理解される物理量の一つです。
表3. 立方晶材料のヤング率の計算値
| 物質 | ヤング率 E (GPa) |
|---|---|
| C (ダイヤモンド) | 936.4 |
| W | 359.9 |
| Fe | 190.5 |
| Si | 124.0 |
| Cu | 103.4 |
| Al | 54.2 |
表3から、ダイヤモンド(C)が他の物質に比べて桁違いに高いヤング率を持つことがわかります。これはダイヤモンドが極めて変形しにくいことを意味し、工業用カッターや研磨剤として利用される理由を裏付けています。金属の中ではタングステン(W)が高い剛性を持ち、鉄(Fe)、銅(Cu)、アルミニウム(Al)の順に柔らかくなっていきます。この序列は、我々の日常的な感覚ともよく一致しています。次に、こうした計算結果の信頼性を左右する、計算手法そのものの影響について見ていきましょう。
テーマ3:計算手法の影響 - GeにおけるGGAとLDAの比較#
第一原理計算において、交換相関汎関数の選択は結果を左右する重要な要素です。本解析ではゲルマニウム(Ge)について、GGA(PBE)とLDAの両方で計算を行いました。表4に、両者の計算結果と実験値を比較します。
表4. Geの体積弾性率における計算手法と実験値の比較
| 計算手法 | 体積弾性率 (GPa) |
|---|---|
| GGA (PBE) | 56.4 |
| LDA | 71.5 |
| 実験値 | 約 75 |
この結果から、LDAを用いた方が実験値に近い値を与えることが分かります。これは、LDAが一般的に原子間距離を短く、結合を強く評価する(過結合傾向)ためです。このように計算手法による結果の違いを理解し、目的に応じて使い分けることが、より精度の高い物性予測に繋がります。
テーマ4:結晶の向きで硬さは変わるか? - 弾性異方性#
材料の硬さ(弾性)は、力を加える方向によって異なる場合があり、この性質を「弾性異方性」と呼びます。ここでは、結晶構造の異なるいくつかの物質を例に、その異方性の度合いをスティフネス定数から見ていきます。
表5. 弾性異方性の議論で用いるスティフネス定数 (GPa)。省略項目は-で示します。
| 物質 | 結晶構造 | c11 | c12 | c33 | c44 |
|---|---|---|---|---|---|
| Si | 立方晶 | 152.8 | 54.6 | - | 102.0 |
| GaN | 六方晶 | 374.7 | - | 366.5 | - |
| Zr | 六方晶 | 148.7 | - | 155.5 | - |
立方晶の場合、異方性の指標としてZener比 () が用いられます。これは という式で定義され、 のときに等方的(どの方向も同じ硬さ)となります。 表5のデータを用いてシリコン(Si)のZener比を計算すると、
となり、1から大きく外れていることがわかります。これは、Siが力を加える方向によって硬さが大きく異なる、強い異方性を持つ材料であることを示しています。
一方、窒化ガリウム(GaN)やジルコニウム(Zr)のような六方晶の場合、底面内(a軸方向)の硬さに関係する と、c軸方向の硬さに関係する を直接比較することで異方性を見ることができます。例えばGaNでは と の値が非常に近く、六方晶であるにもかかわらず弾性的に比較的等方性に近いことが示唆されます。
テーマ5:剛性と靭性の指標 - せん断弾性率とポアソン比#
材料の機械的特性は、体積の変化しにくさ(体積弾性率)だけでなく、形状の変化しにくさ(せん断弾性率)や、一方向に伸ばした際の側方の縮みやすさ(ポアソン比)によっても特徴づけられます。
-
せん断弾性率 (G): 物体の形状を変化させようとする力(ねじり等)に対する抵抗の大きさを示します。値が大きいほど剛性が高く、変形しにくいことを意味します。
-
ポアソン比 (ν): 物体を一方向に引き伸ばしたとき、垂直方向にどれだけ縮むかを示す指標です。一般的に、もろい材料(セラミックスなど)は値が小さく、粘り強い延性材料(金属など)は値が大きくなる傾向があります。
代表的な物質について、これらの値をまとめたのが表6です。
表6. 各種材料のせん断弾性率とポアソン比の計算値
| 物質 | せん断弾性率 G (GPa) | ポアソン比 ν |
|---|---|---|
| C (ダイヤモンド) | 431.3 | 0.086 |
| W | 140.9 | 0.278 |
| Si | 49.1 | 0.263 |
| Al | 19.9 | 0.359 |
| Cs | 0.14 | 0.460 |
この表から、ダイヤモンド(C)は極めて高いせん断弾性率と低いポアソン比を持つことがわかります。これは、ダイヤモンドが非常に変形しにくく(高剛性)、かつ、もろい(低靭性)という性質を的確に反映しています。一方で、アルミニウム(Al)やセシウム(Cs)のような金属は、せん断弾性率が比較的小さく、ポアソン比が0.3以上に達します。これは、これらの材料が変形しやすく、展性や延性に富む(粘り強い)ことを示唆しています。
このように、複数の弾性率を組み合わせることで、材料の多面的な機械的特性を予測し、その物理的背景を深く理解することが可能になります。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて多種多様な材料の弾性定数を計算しました。計算値は実験値と良好な一致を示し、本手法の有効性が確認されました。さらに、得られたデータを様々な角度から分析することで、「物質の硬さの評価」「材料の伸びにくさの序列」「計算手法の選択の重要性」「結晶方位による物性の違い」に加え、「剛性や靭性といった多面的な機械的特性」についても、物性に関する多角的な知見を得ることができました。第一原理計算による弾性定数の予測は、新しい材料の設計や物性メカニズムの解明において、重要な役割を果たすことが期待されます。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
-
W. M. Haynes, ed., CRC Handbook of Chemistry and Physics, 97th ed. (CRC Press, 2016).
-
C. Kittel, Introduction to Solid State Physics, 8th ed. (Wiley, 2005).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学