EELS/XAFSの第一原理計算#

Advance/PHASEは、密度汎関数理論に基づき、平面波基底と擬ポテンシャル法を用いて物質の電子状態をシミュレーションする第一原理計算プログラムです。擬ポテンシャル法は、価電子状態の計算が得意とされますが、内殻電子励起スペクトルの計算にも適用可能です。ここでは、電子線の照射によるEELS（電子エネルギー損失分光）、X線の照射によるXAFS（X線吸収微細構造）スペクトルについて、第一原理計算での計算方法と応用例を紹介します。

Keywords: EELS、XAFS、第一原理計算、密度汎関数理論、平面波基底、擬ポテンシャル法、内殻電子励起、スペクトル

はじめに#

EELS（Electron Energy-Loss Spectroscopy）とXAFS (X-ray Absorption Fine Structure) は、実験手法こそ異なりますが、観測される物理現象の起源や得られる情報は非常によく似ています。そのため、第一原理計算では、これら二つの分光法は共通の理論的枠組みと計算手法を用いてシミュレートされることが一般的です。

第一原理計算ソフトウェアAdvance/PHASEでは、電子状態計算を実行した後、その結果と内殻軌道の波動関数ファイル、そしてコアホール擬ポテンシャルを用いることで、様々な材料のEELSスペクトル（および同様の手法でXAFSスペクトル）を計算することが可能です。ここでは、簡潔さを期すため、主にEELSに焦点を当てて説明します。

EELSの計算方法#

EELSでは、入射電子により試料を構成する系の内殻電子が励起され、伝導帯に遷移します。エネルギー保存則に従いますと、電子線の損失エネルギー( $E$ ) は、系の「基底状態」と「内殻電子が伝導帯に遷移した状態」のエネルギー差に等しく

$E = E_f - E_i \quad (1)$

と書けます。 $E_i$ は初期状態、つまり基底状態のエネルギーです。 $E_f$ は終状態、つまり内殻電子が伝導帯に遷移した状態のエネルギーです。各エネルギーはSCF にて計算可能です。SCF にて計算されたエネルギーの差分を取る方法はΔ-SCF 法と呼ばれ、EELS のスペクトルのピーク位置を定量的に再現することが知られています。

スペクトルの形状について、電子線の損失エネルギー $E$ に対する散乱強度 $I(E)$ はフェルミの黄金律に従う[1]:

$\displaystyle I(E) = \sum_{i,f} \left| \langle i | e^{i\mathbf{q}\cdot\mathbf{R}} | f \rangle \right|^2 \delta(E - (E_f - E_i)) \approx \sum_{i,f} \left| \langle i | \mathbf{q}\cdot\mathbf{R} | f \rangle \right|^2 \delta(E - (E_f - E_i)) \quad (2)$

と書けます。二つ目の等号では、双極子近似を適用しています。ここで、 $\mathbf{q}$ は電子線の運動量変化、 $\mathbf{R}$ は座標演算子です。 $|i\rangle$ は始状態、 $|f\rangle$ は終状態を意味します。一電子近似を用いると、 $|i\rangle$ は内殻原子軌道 $|\phi_{\text{core}}\rangle$ に等しいです。 $|f\rangle$ は、伝導帯の波動関数です。ただし、「内殻電子が伝導帯に遷移した状態」を表現するために、 $|f\rangle$ は内殻正孔擬ポテンシャルを使用したSCF計算、あるいはSCF計算で得られた電荷密度に基づいたnon-SCF計算にて作成されます。また、正確な波動関数の情報を得るためには、PAW法の使用が必須です。

EELSの計算では、周期境界条件を使用しているため、隣接するセルの間で伝導帯に励起された電子同士が影響を及ぼし合います。これにより、計算精度が低下する可能性があります。計算精度を担保するため、スーパーセルを使用することを推奨します。

擬ポテンシャルの作成#

指定原子種の内殻軌道の波動関数ファイルおよびPAW型の内殻正孔（コア・ホール）擬ポテンシャルは、Advance/CIAOを用いて作成可能です。

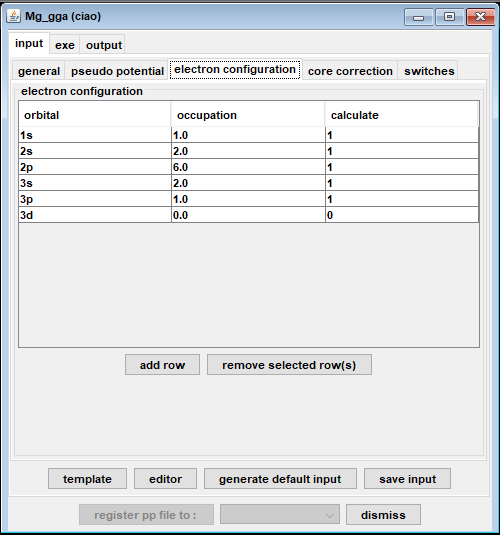
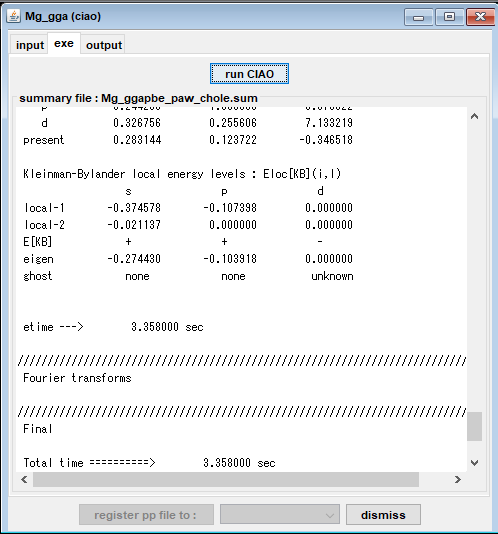
図1は、Advance/PHASEでのCIAOプロジェクトのGUI画面です。(a)は入力画面、(b)は実行画面、(c)は出力画面です。例として、Mgのコア・ホール擬ポテンシャル (1s→3pの内殻励起に対応)の作成手順を示します。まず、元素名を選択して、通常の擬ポテンシャル作成用のインプットファイルが自動的に生成されます。そして、electron configurationに1sと3pの占有数を指定して、さらにスピンを設定すれば、内殻励起した状態に対応する擬ポテンシャルが作成できます。ジョブの実行はすぐ終わるので、直ちに擬ポテンシャルに対する各種解析(ghost状態の有無のチェックなど)ができます。図1(c)は全電子原子軌道と擬原子軌道の比較を示しています。カットオフ半径の外で両者は一致していることや全電子原子軌道p, dがノードを持つことが分かります。

(a)

(b)

(c)

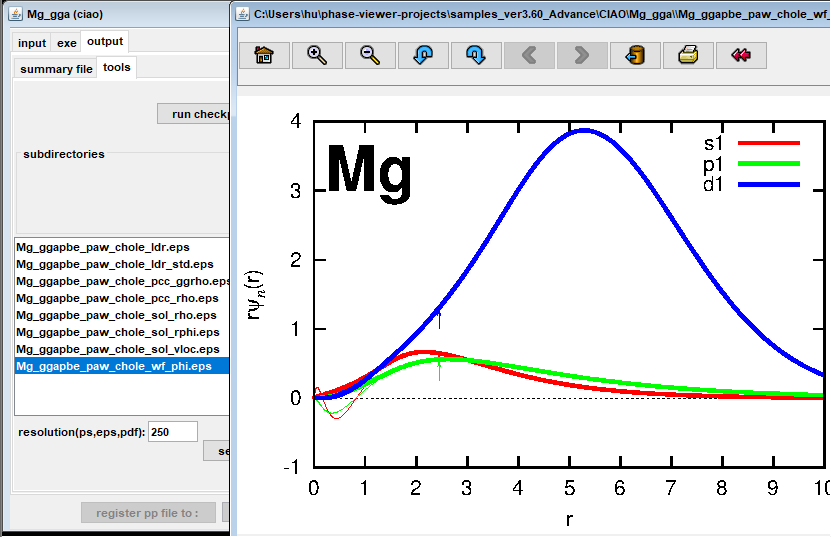
図1．Advance/PHASEのGUIでMgの内殻正孔擬ポテンシャル作成画面 (例は1s→3pのコア励起) (a)入力設定画面 (b)ジョブ実行画面 (c)出力結果解析画面

EELSの計算設定#

Advance/PHASEでは、EELS を計算する原子 1 個のみを内殻正孔擬ポテンシャルを用いて計算するため、計算セルはスーパーセルを使用します。図2 は MgO の計算例を示しています。2×2×2のスーパーセルの中に、注目原子(Mg0)のみにコア・ホール擬ポテンシャルを割り当てます。ほかの原子(MgとO)に対しては、通常の擬ポテンシャルを使用します。

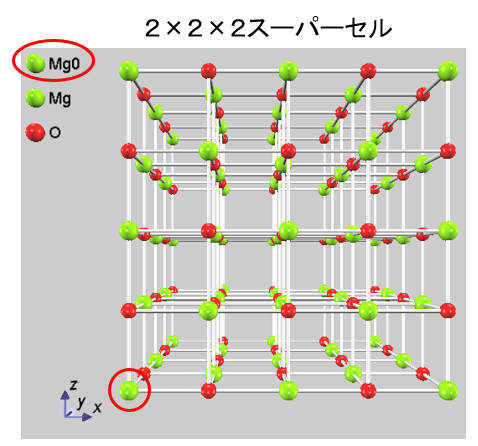
図2．MgOの2×2×2スーパーセル。注目原子(Mg0)にコア・ホール状態の擬ポテンシャルを割り当てます。

実際のEELS計算において、各種設定はGUIで簡単に行えます。図3のように、以下の項目が設定できます：

(1) スペクトルを作成する際の、ピークのスメアリング法；
(2) 価電子軌道に対して相対論補正の適用の有無；
(3) 遷移対象の内殻軌道を含む原子の指定；
(4) 遷移双極子モーメントを計算する内殻軌道の数、名前、エネルギー；
(5) 遷移双極子モーメントを計算する価電子軌道のエネルギー範囲；
(6) 系に含まれる励起電子数（スピンごとに）。

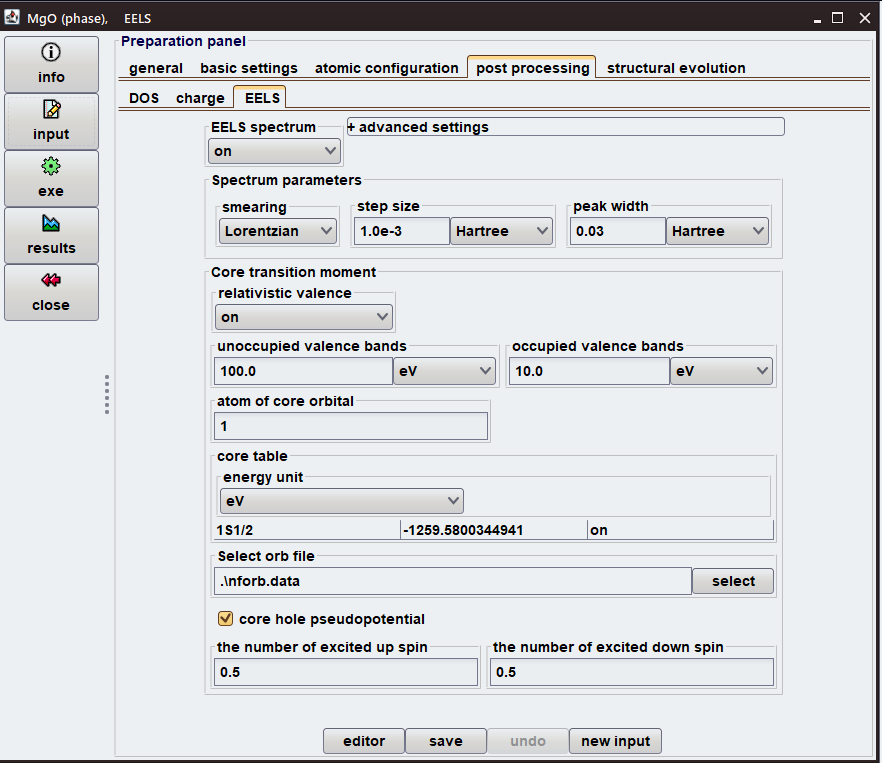
図3．MgOのEELS計算の入力設定パネル

デフォルト設定にて計算を実施すると、電子線の運動量変化について球平均されたスペクトルが出力されます。電子線の運動量変化を明示的に指定したい場合、運動量変化の x , y , z 成分を直接に指定することも可能です。

EELSの計算例#

計算例として、まず、酸化マグネシウム（MgO）のEELS スペクトルを示します（図4）。内殻軌道としては、Mg 原子の1S_1/2 軌道を使用しています（該当のスペクトルは、K 端と呼称されます）。点線は実測結果[2]、赤線・青線はそれぞれ内殻正孔擬ポテンシャル使用あり・なしの計算結果です。内殻正孔擬ポテンシャルを使用したスペクトル計算は実験値をよく再現しています。

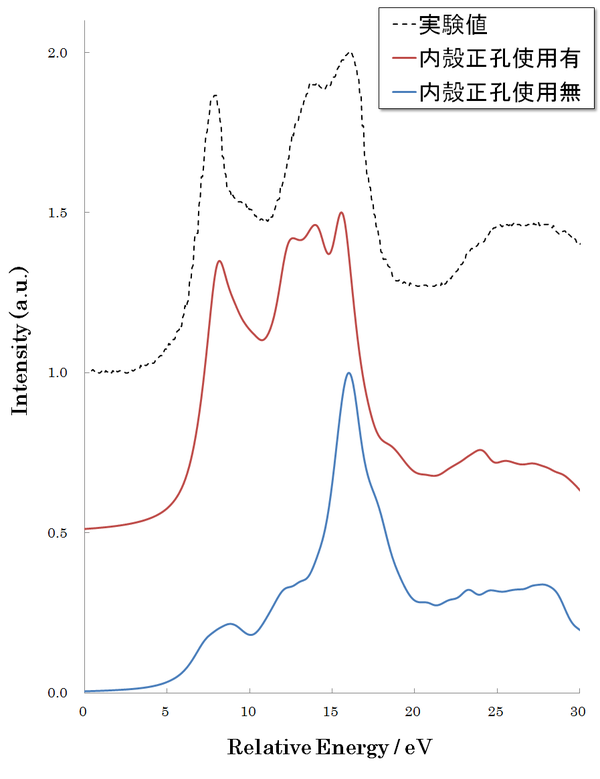
図4．MgOの EELSスペクトル。Mg原子のK端。

次は、炭素材料であるグラファイトとダイヤモンドのEELS計算結果を図5で示します。実測結果[3]のように、グラファイトのほうに特徴的なピーク(赤の点線で囲むもの)があることを計算でよく再現しています。射影状態密度の解析により、これはπ* 状態による吸収であること（隣接原子との化学結合を反映した情報）が分かりました。

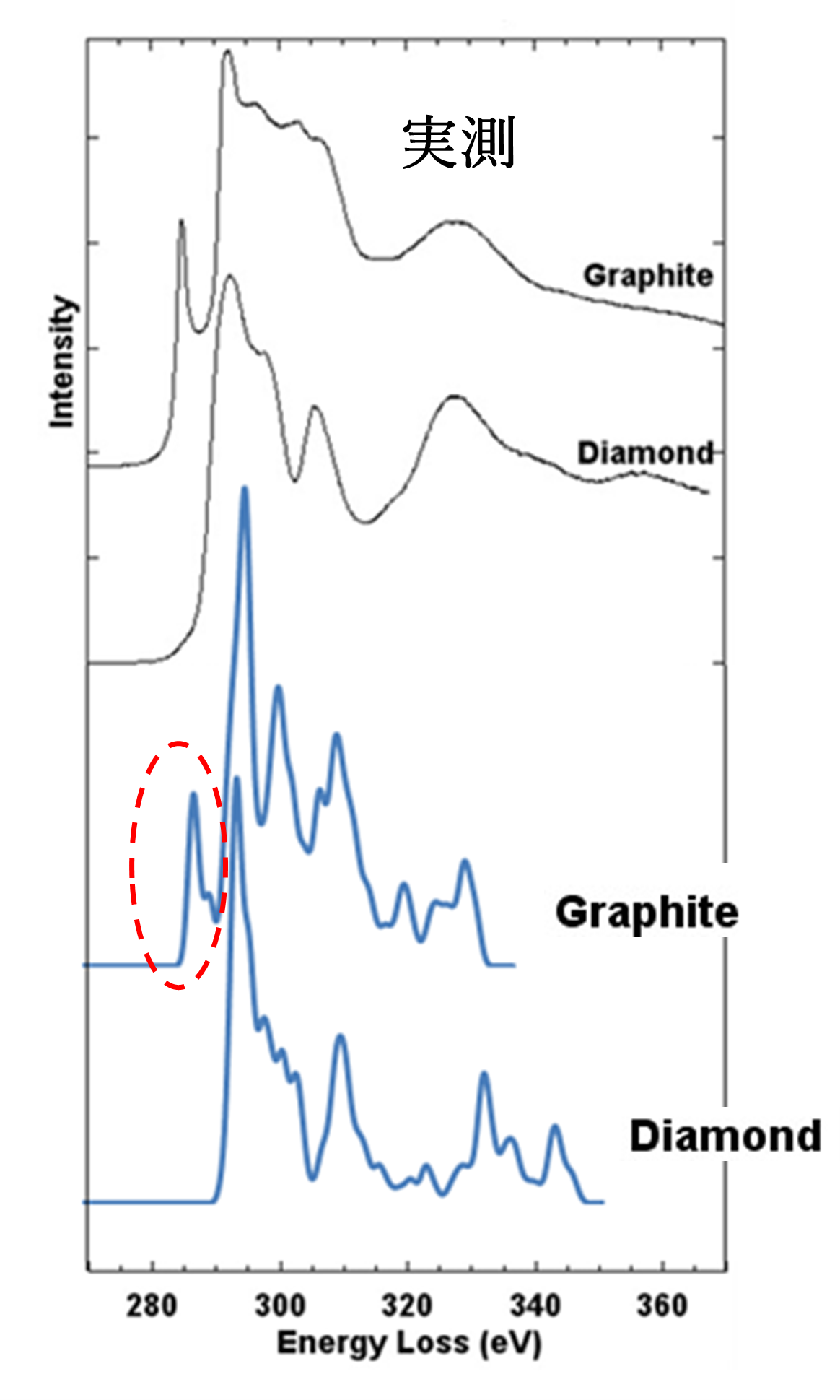
図5．グラファイトとダイヤモンドのEELS（黒線は実測結果、青線は計算結果）

最後に3C-SiCのC K-edge EELSスペクトルを図6で示しています。計算結果は、実測結果[4]の特徴的なピークを再現しています。また、Δ-SCF計算によって、ピークの位置も一致していることがわかります。

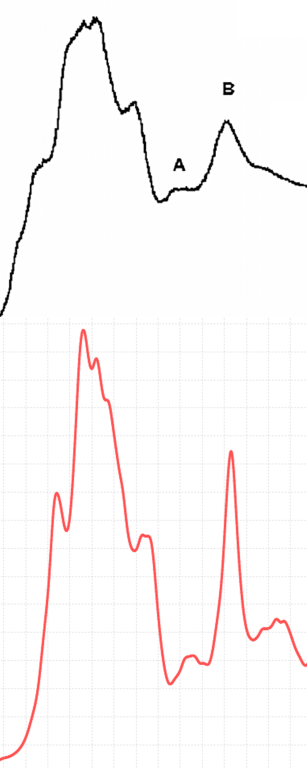
図6．3C-SiC C K-edgeのEELS（黒線は実測結果、赤線は計算結果）

まとめ#

Advance/PHASEでは、密度汎関数理論に基づき、平面波基底と擬ポテンシャル（内殻正孔擬ポテンシャルとの併用）を用いた第一原理計算で、EELS (XAFS) スペクトルを精度よくシミュレーションできます。擬ポテンシャル作成プログラムAdvance/CIAOの標準搭載により、一層の利便性・効率性の向上が期待されています。

参考文献#

S. P. Gao, C. J. Pickard, M. C. Payne, J. Zhu, J. Yuan, Phys. Rev. B 77 (2008) 115122.
Th. Lindner, H. Sauer, W. Engel, and K. Kambe, Phys. Rev. B 33 (1986) 22.
https://muller.research.engineering.cornell.edu/spectra/graphite-and-diamond-c-k-edge-spectra
M Pedio et al., Physica Scripta T115 (2005) 308.