DFT+U法の解析事例：ペロブスカイト化合物への適用#

ペロブスカイト化合物は、その組成や構造、元素によって様々な電子的な性質を示すことがあり、強相関、超伝導など、多様な物性を持つ可能性を秘めています。第一原理計算が立脚する密度汎関数(DFT)法は、強相関ペロブスカイト系において局所密度近似で電子相関を正確に記述していないことが知られています。DFT+U法は、通常のDFT法にオンサイトクーロン相互作用による補正を加えることで、これらの物質へ適用可能にする手法です。ここでは、Advance/PHASEに実装されたDFT+U法による解析事例を紹介し、バンドギャップのみならず、局在磁気モーメント間の相互作用が精度よく得られる点を示します。

Keywords: 第一原理 (First-principles calculation), DFT+U 法, 交換相互作用パラメータ (spin-exchange parameter)

DFT+U法#

DFT+U法では、同一原子上の同一各運動量を持つ軌道にある電子間の反発エネルギーを $U_{\text{eff}}$ として、これを全エネルギーに加えます。補正後の全エネルギー $E_{\text{DFT+U}}$ は

$E_{\text{DFT+U}} = E_{\text{DFT}} + \frac{U_{\text{eff}}}{2}\sum_I\sum_{m,\sigma}\left\{\rho^{I\sigma}_{m,m} - \sum_{m'}\{\rho^{I\sigma}_{m,m'}\rho^{I\sigma}_{m',m} \}\right\} \quad (1)$

と表わされます。ここで、 $I$ は3d金属原子等の局在電子をもつ原子があるサイト、 $m$ ( $m’$ ) は対応する軌道の磁気量子数、 $\sigma$ はスピン( $\uparrow, \downarrow$ )です。 $\rho$ は占有行列とよばれ、原子付近の局在軌道 $\chi$ に射影した密度行列です。

$\rho^{I\sigma}_{m,m'} = \sum_{n\mathbf{k}} f_{n\mathbf{k}\sigma} \langle \psi_{n\mathbf{k}\sigma} | \chi^I_{m} \rangle \langle \chi^I_{m'} | \psi_{n\mathbf{k}\sigma} \rangle \quad (2)$

ここで、 $n, \mathbf{k}$ は電子状態の波数ベクトル及びバンド指標に対応し、また $f_{n\mathbf{k}\sigma}$ はその占有数です。

ペロブスカイトKCuF₃への適用事例#

ペロブスカイトKCuF₃結晶の協調的ヤーンテラー変形、及びスピン交換相互作用について紹介します。KCuF₃は、ヤーンテラーイオンであるCu 原子を含むため、F原子が協調的に変位した歪んだ構造をとることが知られています。この際、F原子間の距離には長短が生じ、最短の距離は図1の八面体の中心を通る太実線のように、隣接するセル間で異なる方向にならびます。同時に、電子状態においては、占有されるCuの3d軌道（e_g軌道）の向きがセル間で異なるよう整列します。このような軌道整列とともに、低温ではc軸方向に反強磁性秩序を形成することが知られています。以下では、軌道整列秩序及びスピン交換相互作用について、DFT+U法による計算結果と実験との一致を報告します。

格子定数として、実験値 (a,b 軸方向: 4.149 Å、c軸方向: 3.936 Å) を採用しました [1]。波動関数と電荷のカットオフは、それぞれ25 及び350 Ryです。電子状態の収束条件は、10^-8 Hartreeとしました。擬ポテンシャルとしてK、Cu、F 原子いずれも超ソフトポテンシャルを採用し、交換相関相互作用には GGAPBE汎関数を用いました。 $U_{\text{eff}}$ の値は、Cu 3d軌道に対して6.6 eV [2] を用いました。

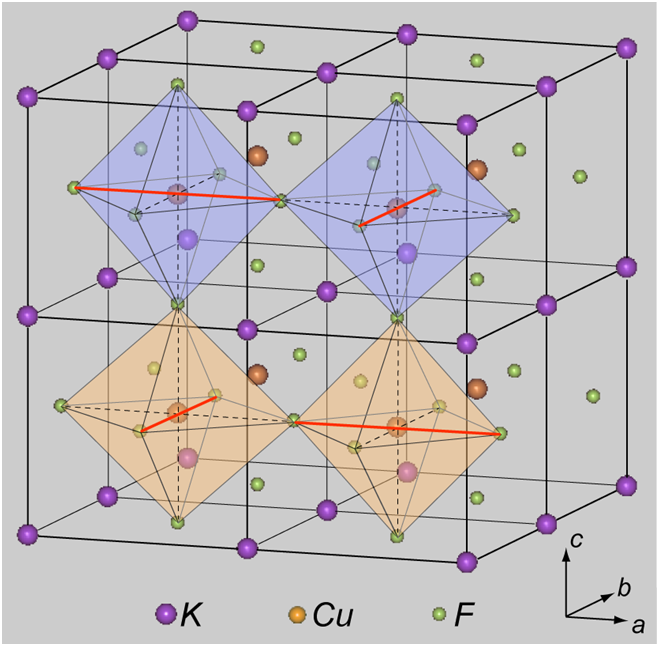
図1．KCuF₃ 結晶構造。c軸方向がa、b 軸方向に比べて短いです。影をつけた八面体の中心及び頂点の原子はCuおよびF原子です。八面体の中心を通る太線は、F原子間の距離が最短となるものを示します。

ヤーンテラー歪#

最初に、計算で確認された軌道秩序の形状を図2に示します。F-type軌道秩序は、スピン密度の広がる方向がc軸方向となるのに対し、G-type軌道秩序は隣接する格子間で直交しています。特に、後者についてe_g 軌道の名称でいえば、d_z²-x² と d_z²-y² が交互に並んでいます。実験ではG-type軌道秩序が観測されています。

さて、KCuF₃はヤーンテラー歪によりCu – Fボンド長に長短が生じるわけですが、格子歪みの指標として

$\delta_{\text{JT}} = \dfrac{1}{2}\dfrac{d_l - d_s}{d_l + d_s} \quad (3)$

を定義します。ここで、 $d_l$ 及び $d_s$ は、ab 面上における Cu – F ボンドのうち、長短のボンド長を指します。

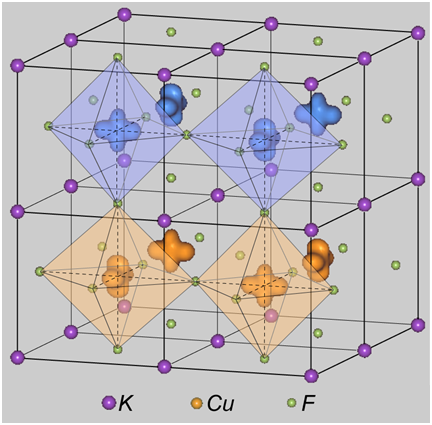
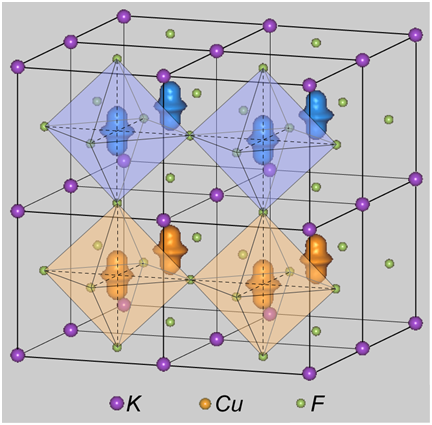
図2．KCuF₃内の (左) F-type 軌道秩序及び (右) G-type 軌道秩序。Cu 原子付近のアップ及びダウンスピン密度分布を、色の異なる２つの領域として示しました。なお、c軸方向には、反強磁性磁気秩序 ( A-type ) があるとしました。

図3は、格子歪み $\delta_{\text{JT}}$ をパラメータとしてエネルギーをプロットしたものです。左図は $U_{\text{eff}}$ = 0.0 eV、右図は $U_{\text{eff}}$ = 6.6 eVに対応します。黒丸及び赤丸の点は、反強磁性 (A-type) 及び強磁性秩序の場合です。すなわち、前者はc軸方向に層ごとの磁気モーメントの向きが反転しますが、後者は全て揃った場合に相当します。なお、いずれの場合もab 面内の磁気モーメントの向きは揃っているものとします。

さて、F-type軌道秩序は $U_{\text{eff}}$ = 0 eVでは見られませんが、 $U_{\text{eff}}$ = 6.6 eVでは $\delta_{\text{JT}}$ < 2.2 %の領域でのみ安定な状態として得られました（図3(b)の四角点）。一方、G-type軌道秩序に対応する黒丸及び赤丸の点を比較しますと、 $\delta_{\text{JT}}$ の値によらず黒丸の点、すなわちc軸方向に反強磁性秩序を取る状態が安定なことが分かります。従って、エネルギー的に最安定なのはG-typeの反強磁性状態で、格子歪み $\delta_{\text{JT}}$ は3.4 % ( $U_{\text{eff}}$ = 0 eV) 及び 3.0% ( $U_{\text{eff}}$ = 6.6 eV) です。

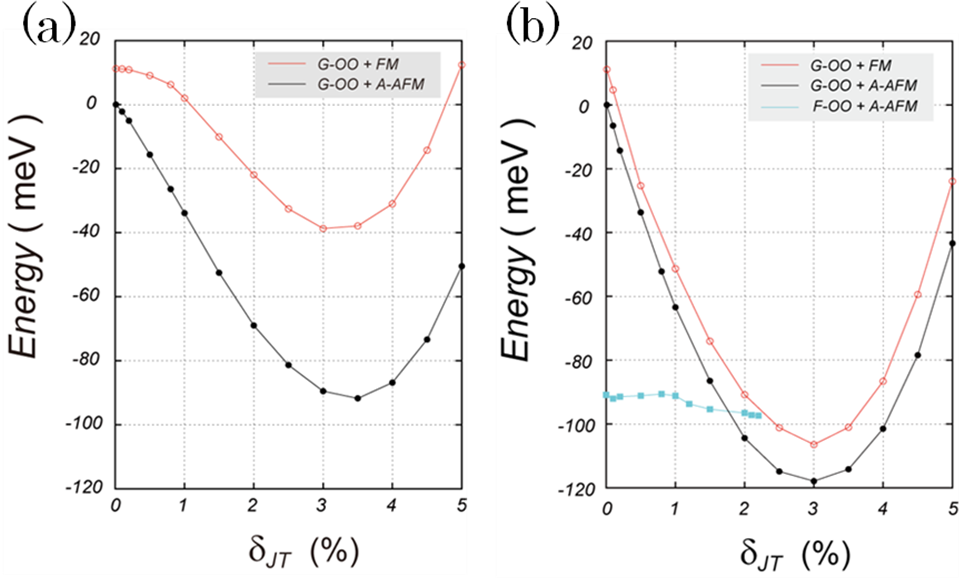
図3．格子歪みに対するCu１原子あたりのエネルギー変化。（a）U_eff = 0 eV、(b) U_eff = 6.6 eVです。G(F)-OO はG(F)-type 軌道秩序 (Orbital Ordering)、A-AFM はA-type反強磁性秩序、FM は強磁性秩序を意味します。反強磁性 ( A-type ) 及び強磁性秩序は黒丸及び赤丸で表示しました。

スピン交換パラメータ#

G-type軌道秩序のもとで、強磁性と反強磁性状態（A-type）のエネルギー差からc軸方向のスピン交換パラメータ J が得られます。ここでJ は

$H = J \sum_{\langle i,j \rangle} \mathbf{S}_i \cdot \mathbf{S}_j \quad (4)$

で定義されます。 $\mathbf{S}_i$ の大きさは 1/2 で、また、 $\sum_{\langle i,j \rangle}$ は最近接相互作用のみの和を意味します。表1に、 $U_{\text{eff}}$ = 6.6 eVで得られた J の値と実験値を比較しました。

表1．スピン交換相互作用 J の値。

	J [meV]
本計算	24.66
実験値[2]	29.04-34.99
実験値[3]	26.0

G-type 軌道秩序及びA-type 反強磁性秩序をもつ状態で最適化した構造 ( $\delta_{\text{JT}}$ = 3.0%) を用いて計算しますと、J = 24.66 meV が得られました。実験値は、26.0から34.99 meVまでの範囲で報告されており、計算はこれを再現しているといえます。一方、 $U_{\text{eff}}$ = 0 eVの場合には、図3(a）より J = 100 meV 程度と見積もられます。Jの値の過大評価は、磁気相転移温度を不正確に与えることになり、DFT+U法による補正が重要なことを意味しています。

電子状態#

最後に、電子状態密度について記述します。図4(a)は -5 < E < 5 eV付近の電子状態密度を示します。

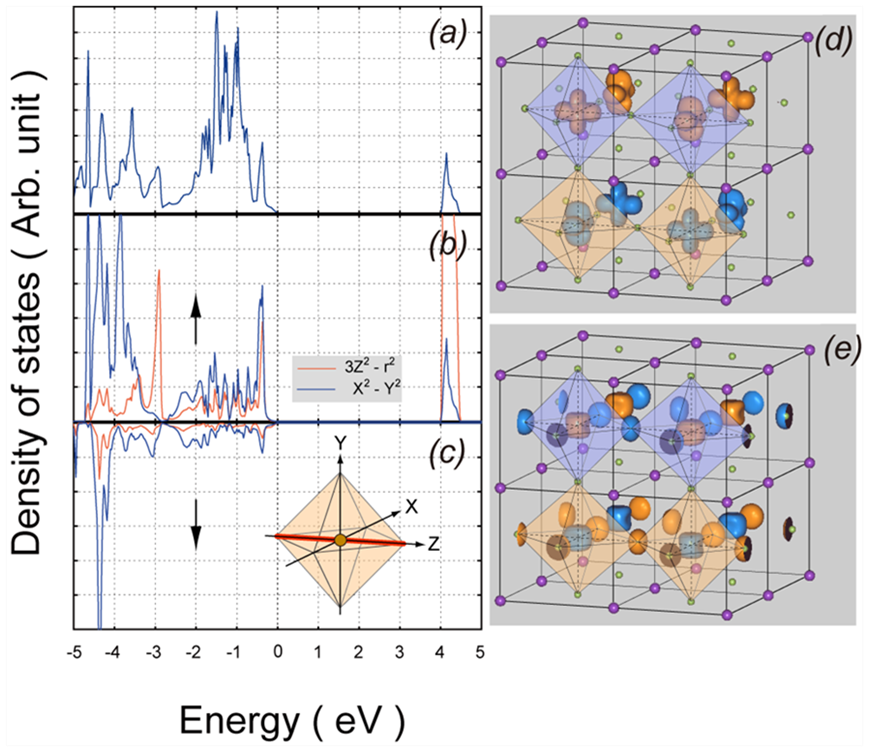
図4 (a)電子状態密度。 (b,c) e_g 軌道に射影した状態密度。局所座標系は (c)の内挿図で定義しました。(b)はアップスピン、(c)はダウンスピンに対応します。(d) 4 < E < 5 eV の積分状態密度、(e) -2 < E <-1 eVの積分状態密度。色の違いは、上向き及び下向きスピンに対応します。

E = 0 eVは価電子帯上端のエネルギーに対応します。伝導帯下端は E = 4 eV付近で立ち上がっており、ギャップは約4.0 eVです。なお、 $U_{\text{eff}}$ = 0 eV におけるギャップは0.5 eVであり、 $U_{\text{eff}}$ の効果により約 3.5 eV増加しています。（実測値は報告されていません。）図4(b)及び図4(c)は、あるCu 原子近辺の状態密度をe_g 軌道に射影した状態密度です。前者がアップスピン、後者がダウンスピンに対応します。ここで、局所座標系は図4(c)内挿図のように定義し、Cu – F ボンドが最短になる方向をZ軸としました。アップスピンの状態密度の4 < E < 5 eV付近のピークはいわゆる上部ハバードバンドに対応します。これに対応して、下部ハバードバンドは E < -5 eVに出現しますが、ここでは表示していません。

図4(d)は、電子状態密度を 4 < E < 5 eVの範囲で積分したもので、上部ハバードバンドの空間分布を示しています。色の2種類のローブ状領域はそれぞれアップ・ダウンスピンに対応します。図4(b)および図4(c)の電子密度分布に似ていますが、下部ハバードバンドが占有されていることを反映して逆位相になっています。図4(e)は -2 < E < -1 eVの範囲で積分した状態密度の空間分布を示し、このエネルギー領域でFの2p軌道とCuの3d軌道の混成が生じていることを示しています。

同様な状態密度分布は他の理論計算でも報告されており、妥当な結果を与えているといえます。

まとめ#

電子相関の強い系に対しては、DFT法は局所密度近似でギャップを正確に求められないなど限界があることが知られています。一方、電子間の反発による補正を取り入れたDFT+U法では、この点が改善されることが知られています。ここでは、Advance/PHASEに実装したDFT+U法の解析例を紹介し、バンドギャップ以外にも、局在磁気モーメント間相互作用が精度よく得られる点を示しました。

参考文献#

C. Oliva, M. Scavini, S. Cappelli, C. Bottalo, C. Mazzoli, and P. Ghigna. J. Phys. Chem. B 111 (2007) 5976.
I. d. P. R. Moreira and F. Illas. Phys. Rev. B 60 (1999)5179 and references therein.
D. A. Tennant, S. E. Nagler, D. Welz, G. Shirane, and K. Yamada. Phys. Rev. B 52 (1995) 13381.

DFT+U法の解析事例： ペロブスカイト化合物への適用#