DFT+U法の解析事例：遷移金属酸化物への適用#

第一原理計算が立脚する密度汎関数 (DFT) 法は、遷移金属酸化物等の系で局所密度近似が電子相関を正確に記述していないことが知られています。DFT+U法は、通常のDFT法にオンサイトクーロン相互作用による補正を加えることで、これらの物質へ適用可能にする手法です。ここでは、Advance/PHASEに実装されたDFT+U法による解析事例を紹介し、バンドギャップのみならず、電子・格子誘電率が精度よく得られる点を示します。

Keywords: 第一原理 (First-principles calculation), DFT+U 法, 誘電率 (dielectric properties)

DFT+U法#

DFT+U法では、同一原子上の同一各運動量を持つ軌道にある電子間の反発エネルギーを $U_{\text{eff}}$ として、これを全エネルギーに加えます。補正後の全エネルギー $E_{\text{DFT+U}}$ は

$E_{\text{DFT+U}} = E_{\text{DFT}} + \frac{U_{\text{eff}}}{2}\sum_I\sum_{m,\sigma}\left\{\rho^{I\sigma}_{m,m} - \sum_{m'}\{\rho^{I\sigma}_{m,m'}\rho^{I\sigma}_{m',m} \}\right\} \quad (1)$

と表わされます [1-2]。ここで、 $I$ は3d金属原子等の局在電子をもつ原子があるサイト、 $m$ ( $m’$ ) は対応する軌道の磁気量子数、 $\sigma$ はスピン( $\uparrow, \downarrow$ )です。 $\rho$ は占有行列とよばれ、原子付近の局在軌道 $\chi$ に射影した密度行列です。

$\rho^{I\sigma}_{m,m'} = \sum_{n\mathbf{k}} f_{n\mathbf{k}\sigma} \langle \psi_{n\mathbf{k}\sigma} | \chi^I_{m} \rangle \langle \chi^I_{m'} | \psi_{n\mathbf{k}\sigma} \rangle \quad (2)$

ここで、 $n, \mathbf{k}$ は電子状態の波数ベクトル及びバンド指標に対応し、また $f_{n\mathbf{k}\sigma}$ はその占有数です。

遷移金属酸化物NiOへの適用事例#

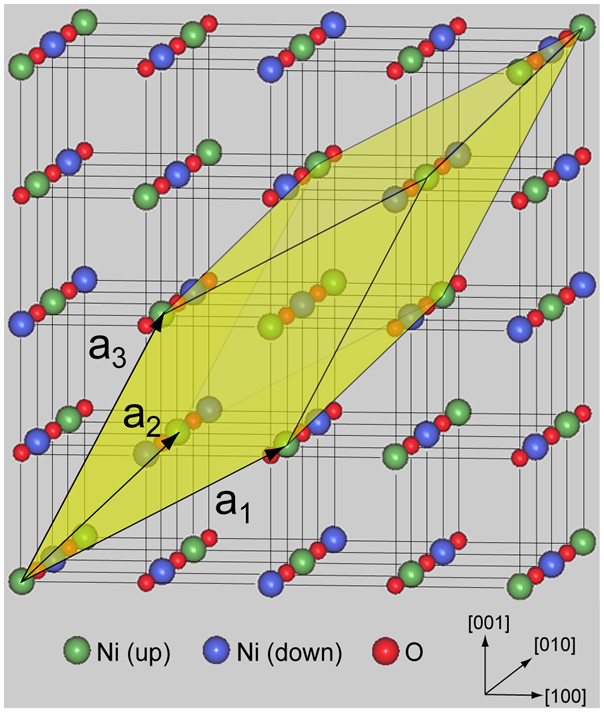
図1．cubic NiO構造。色の異なる大きい球はNi原子で、それぞれ磁気モーメントの向きが異なります。小さい球はO原子です。計算に用いた単位胞は影を付けた菱面体領域で、a₁、a₂、a₃は格子ベクトルです。

図 1は、cubic構造のNiO結晶で、大きい球はNi原子、小さい球はO原子に対応します。Ni原子上の磁気モーメントは、低温では (111)面に平行な面上で整列し、かつ隣接する面間ではその向きが逆となる構造をとることが知られています（type-IIの反強磁性、AF-II）。この磁気秩序を表示するため、上及び下向きの磁気モーメントをもつNi原子を色の違う球で表示しています。計算に用いた単位胞は影を付けた菱面体領域で、a₁、a₂、a₃ は対応する格子ベクトルです。

格子定数は文献値4.1770 Å [3] を採用しました。

擬ポテンシャルとしてNi、O原子いずれも超ソフトポテンシャルを採用し、交換相関相互作用にはGGAPBE汎関数を用いました。波動関数と電荷のカットオフはそれぞれ30及び360 Ryとし、電子状態の収束条件は10^-8 Hartreeとしました。有効ハバード相互作用 $U_{\text{eff}}$ は、Ni 3d軌道に対して $U_{\text{eff}}$ = 0 – 8 eVを試しました。

電子状態密度#

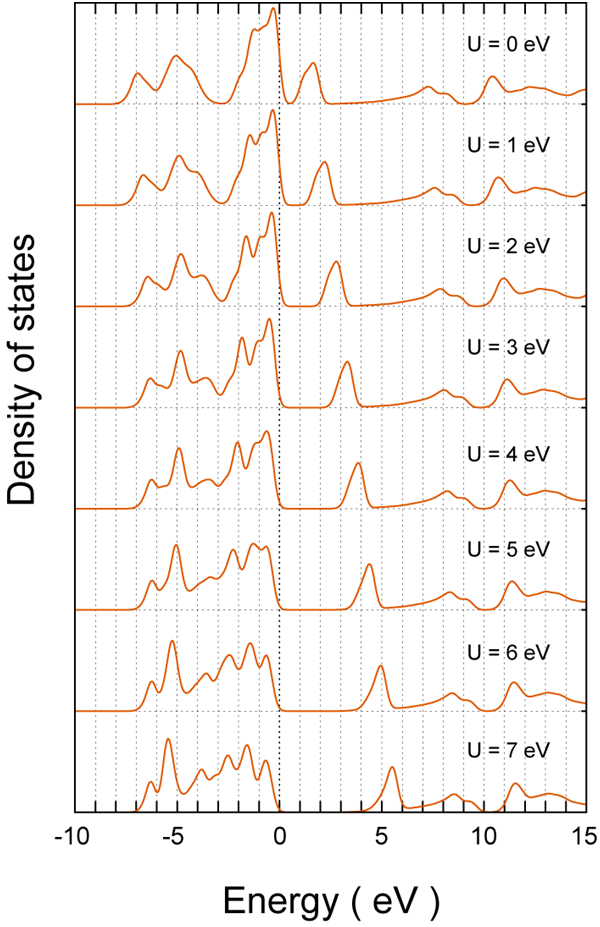
図2．NiOの電子状態密度。 $U_{\text{eff}}$ の値は、上から順に0 から7eVまで1 eV刻みで変化させています。

図 2は電子状態密度で、上から順に $U_{\text{eff}}$ = 0 から 7 eV まで1 eV 刻みで変化させています。ただし、各状態密度はgaussian ( $\sigma$ = 0.2 eV) により滑らかに調整して表示し、Energyの原点は価電子帯上端にとっています。 $U_{\text{eff}}$ の増加とともに、伝導帯の第1ピークが高エネルギー側に移動する様子がわかります。

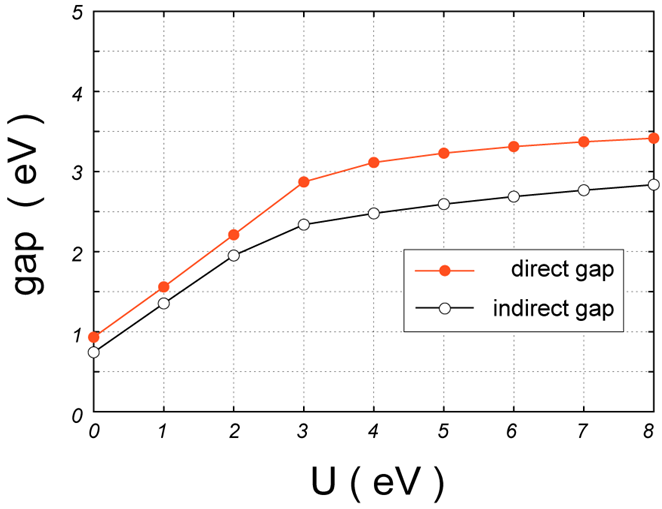
図3．NiO結晶におけるバンドギャップの大きさの $U_{\text{eff}}$ 依存性。赤丸及び白丸は、直接及び間接ギャップ。

図 3は、価電子帯上端と伝導帯下端の間のギャップ値について、 $U_{\text{eff}}$ 依存性をプロットしたものです。赤丸及び白丸は、それぞれ直接及び間接ギャップに対応します。例えば $U_{\text{eff}}$ = 7 eVの場合、直接ギャップは3.42 eV、間接ギャップは2.77 eV存在します。一方、図 2では、 $U_{\text{eff}}$ = 7 eVにおける伝導帯の第1ピークは4.0 eV付近から立ち上がっているように見えます。これは、2.77 – 4.0 eV間の伝導帯は存在するものの、その状態密度が小さいことを意味しています。

バンド構造#

伝導帯底付近の状態密度が少ない原因を調べるため、バンド構造計算を行いました。例として $U_{\text{eff}}$ = 5 eVにおけるバンドを図 4に示します。

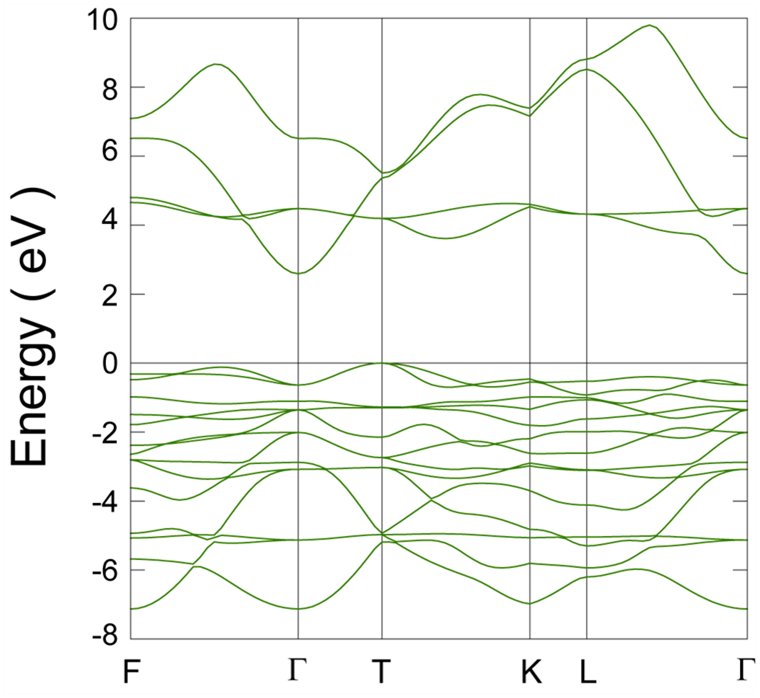
図4． $U_{\text{eff}}$ = 5 eVにおけるNiO結晶のバンド構造。エネルギーの原点は、価電子帯上端にとりました。

F点で最もエネルギーの低い2本の伝導バンド (ほぼ縮退) は、Brillouin zone内の位置依存性が少なく、大きな状態密度を与えます。一方、Γ点にて伝導帯下端を形成するバンドはBrillouin zoneの中で最小のエネルギーをもちますが、Γ点から離れるにつれて急速にエネルギーが増加します。すなわち、このバンドはバンド幅が広いものの、伝導帯下端付近の状態密度への寄与は小さいです。結果、前者は図 2の伝導帯の第1ピークを与えますが、後者はこのピークの裾に埋もれてしまいます。

電子誘電率#

電子誘電率の虚部を図 5に示します。横軸はフォトンのエネルギーに対応します。 $U_{\text{eff}}$ の値は(a) 0 – 4 eV、(b) 5 – 8 eVです。 $U_{\text{eff}}$ の増加に伴いピーク位置が高エネルギー側に移動することが分かります。また、ピークの立ち上がり位置も同様の振る舞いを示しますが、 $U_{\text{eff}}$ > 4eVではほとんど変化しなくなります。このような飽和した挙動は、図 3にてバンドギャップの大きさが $U_{\text{eff}}$ > 4eVではあまり増加しないことより理解されます。

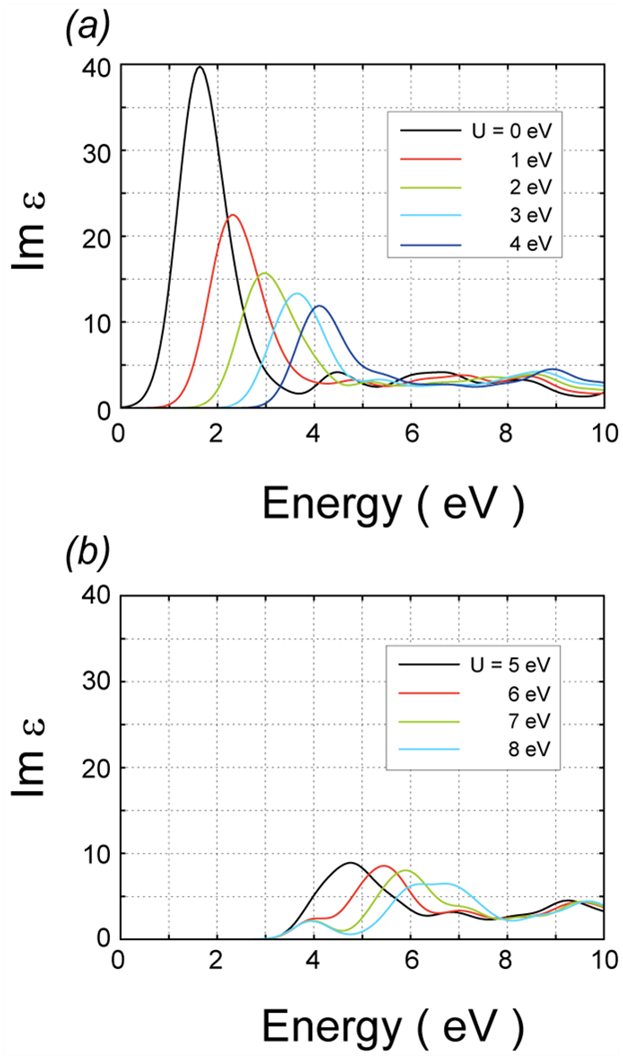
図5．NiOの電子誘電率虚部。 $U_{\text{eff}}$ の値は (a) 0 – 4eV、(b) 5 – 8 eV。

さて、図 6は、いくつかの $U_{\text{eff}}$ について計算結果を実験結果[4]と比較したものです。

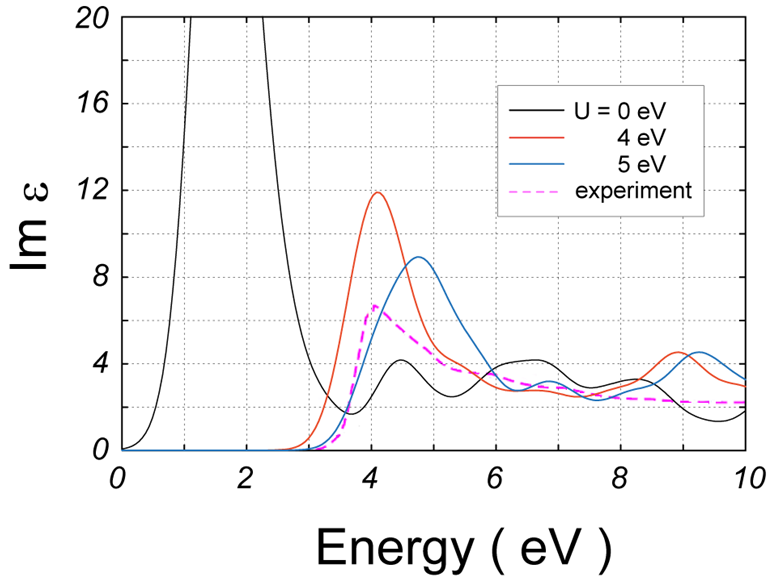
図6．NiOの電子誘電率虚部の実験との比較。点線は実験値です。

$U_{\text{eff}}$ = 0 eVでは全く実験結果を再現しませんが、 $U_{\text{eff}}$ = 4 eVではピーク位置が観測値に近くなります。 $U_{\text{eff}}$ = 5 eVでは、ピーク位置は高エネルギー側に移動してしまうものの、その立ち上がりの挙動が観測結果に似てきます。これらから、電子誘電率の実験結果を再現するには、 $U_{\text{eff}}$ = 4 – 5 eVが望ましいと考えられます。

格子誘電率#

格子誘電率の計算には、まずベリー位相計算によりボルン有効電荷を求めます。格子誘電率の周波数( $\omega$ )依存性が計算可能ですが、実験との比較のためには、 $\omega$ = 0で格子誘電率と電子誘電率実部の和より静的誘電率を算出します。

なお、電子誘電率における議論で、 $U_{\text{eff}}$ = 4 – 5 eVが妥当とされたので、ここでは $U_{\text{eff}}$ = 5.0 eVを適用します。

得られたボルン有効電荷テンソルは、

$Z^*_{\text{Ni}} = \begin{pmatrix} 2.08 & 0.01 & 0.01 \\ 0.01 & 2.08 & 0.01 \\ 0.01 & 0.01 & 2.08 \end{pmatrix} \quad (3)$

$Z^*_{\text{O}} = \begin{pmatrix} -2.08 & -0.01 & -0.01 \\ -0.01 & -2.08 & -0.01 \\ -0.01 & -0.01 & -2.08 \end{pmatrix} \quad (4)$

です。式(3) の対角成分の絶対値 2.08は、フォノン分散等の実験値から求められた Z*の絶対値2.2 [5]に近く、DFT+U法においてベリー位相計算が正しく行われたことを意味します。

次に、フォノン計算を行い格子誘電率テンソル $\epsilon^{\text{ion}}$ を求めますと、

$\epsilon^{\text{ion}} = \begin{pmatrix} 4.04 & 0.12 & 0.12 \\ 0.12 & 4.04 & 0.12 \\ 0.12 & 0.12 & 4.04 \end{pmatrix} \quad (5)$

が得られました。一方、電子誘電率テンソル $\epsilon^{\text{el}}$ は、電子誘電率の実部を $\omega$ = 0 にて評価しますと、

$\epsilon^{\text{el}} = \begin{pmatrix} 5.50 & -0.08 & -0.08 \\ -0.08 & 5.50 & -0.08 \\ -0.08 & -0.08 & 5.50 \end{pmatrix} \quad (6)$

です。両者を合計しますと、対角項は9.54 となります。なお実験的に得られた静的誘電率は $\epsilon_0$ = 9.1 (温度0Kへの外挿値) [6]であり、同程度の値となっています。

まとめ#

電子相関の強い系に対しては、DFT法は局所密度近似でバンドギャップを正確に求められないなど限界があることが知られています。一方、電子間の反発による補正を取り入れたDFT+U法では、この点が改善されることが知られています。ここでは、Advance/PHASEに実装したDFT+U法の解析例を紹介し、バンドギャップ以外にも電子・格子誘電率が精度よく得られる点を示しました。

参考文献#

S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys, and A. P. Sutton, Phys. Rev. B 57, 1505 (1998).
B. Amadon, F. Jollet, and M. Torrent, Phys. Rev. B 77, 155104 (2008).
S. Iinou, N. Motohira, N. Kamiya, and K. Ota, Bull. Chem. Soc. Jpn 72, 321 (1999).
D. R. Lide, CRC Handbook of Chemistry and Physics, 79th ed. (CRC, Boca Raton, FL, 1998/1999).
R. J. Powell and W. E. Spicer, Phys. Rev. B 2, 2182 (1970).
K. V. Rao and A. Smakula, J. Appl. Phys. 36, 2031 (1965).

DFT+U法の解析事例： 遷移金属酸化物への適用#