vdW相互作用の低コスト高精度計算：ベンゼン二量体と多層グラフェンへのDFT-D法の適用#

第一原理的にファンデルワールス（vdW）相互作用を取り扱うvdW-DF法は信頼性の高い計算手法ですが、計算コストが高く、大規模な系の構造最適化や第一原理分子動力学計算への適用は難しいという課題があります。この課題を解決するため、より低コストでvdW相互作用を扱える手法としてDFT-D法があります。本稿では、第一原理計算ソフトウェアAdvance/PHASEに実装されたDFT-D法が分子間相互作用や層状物質の記述において、高精度な計算結果を効率的に得られることを、ベンゼン二量体および多層グラフェンの計算事例を通して示します。

Keywords: DFT-D, ファンデルワールス相互作用, ベンゼン, グラフェン, ベンチマーク計算

理論背景#

DFT-Dは、その名の通り、密度汎関数理論（DFT）に分散力（Dispersion）の補正エネルギーを経験的に加える手法です。エネルギーは、通常のDFT計算で得られるエネルギー $E_{\text{DFT}}$ と、古典的な分子力場で計算されるvdWエネルギー ( $E_{\text{disp}}$ ) の和で表現されます。

$E_{\text{DFT-D}} = E_{\text{DFT}} + E_{\text{disp}}$

このアプローチにより、DFTが苦手とする長距離のファンデルワールス相互作用を、原子核座標のみに依存する経験的な補正項で補完します。この補正項の計算コストは極めて低いため、構造最適化や分子動力学計算にも容易に適用可能です。

DFT-Dにはいくつかのバージョンが存在し、本稿では主に以下の3つを扱います[1-3]。

DFT-D2: 初期のバージョンで、多くの系で有効ですが、パラメータの適用範囲や原子の化学的環境を考慮していない点に限界があります。
DFT-D3: D2を大幅に改良したバージョンです。より多くの元素に対応し、原子の配位数を考慮することで精度が向上しています。
DFT-D3(BJ): D3の短距離相互作用の記述を、BeckeとJohnsonが提唱したダンピング方式で改良したものです。

ベンチマーク計算：ベンゼン二量体#

DFT-D法の精度を検証するため、代表的なπ-π相互作用系であるベンゼン二量体のポテンシャルエネルギー曲面を計算し、高精度な参照値であるCCSD(T)/CBSの結果と比較しました。計算モデルとして、図1に示す3種類の配向（(a) Sandwich型, (b) T字型, (c) Parallel-Displaced型）を用いました。

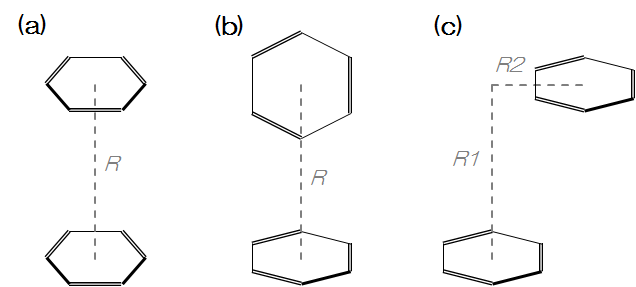
図1.　ベンゼン二量体の構造。(a)Sandwich型、(b)T字型、(c)Parallel-Displaced型。

図2、3、4に各配向での計算結果を示します。いずれの図からも、下記のような共通した特徴が見られます。

PBE（補正なし）: 赤い線で示されるPBE汎関数（分散力補正なし）の結果では、ベンゼン間に引力的な相互作用がほとんど現れず、結合エネルギーを正しく記述できていないことがわかります。
DFT-D補正: 青、黄、緑の線で示されるDFT-D2, D3, D3(BJ)を適用した結果は、いずれも黒い線で示される高精度なCCSD(T)の結果を非常によく再現しています。これにより、経験的ながらもDFT-D補正がvdW相互作用を的確に記述できることが確認できます。
手法間の比較: 特にDFT-D3およびDFT-D3(BJ)は、結合エネルギーと平衡距離の両方において、CCSD(T)の結果と高い一致を示しています。紫の線で示されるvdW-DFも良好な結果を与えていますが、DFT-D法が同等以上の精度をより低い計算コストで達成できることは大きな利点です。

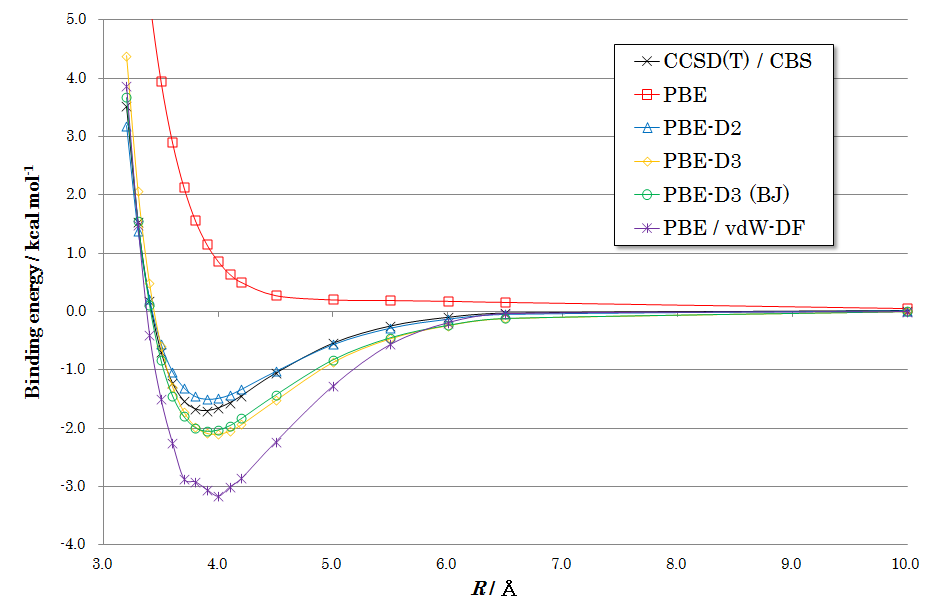
図2.　Sandwich型ベンゼン二量体のポテンシャル曲面

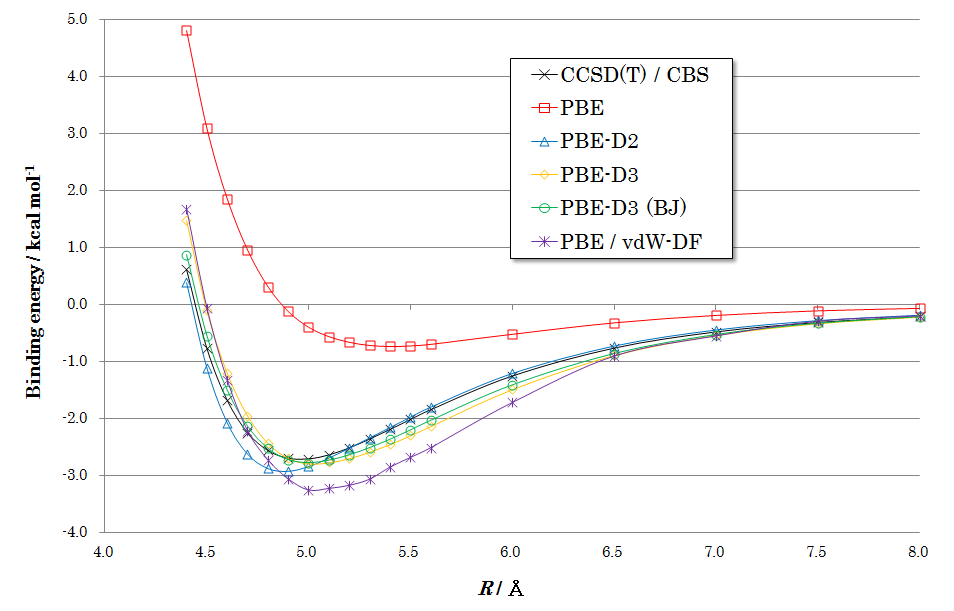
図3.　T字型ベンゼン二量体のポテンシャル曲面

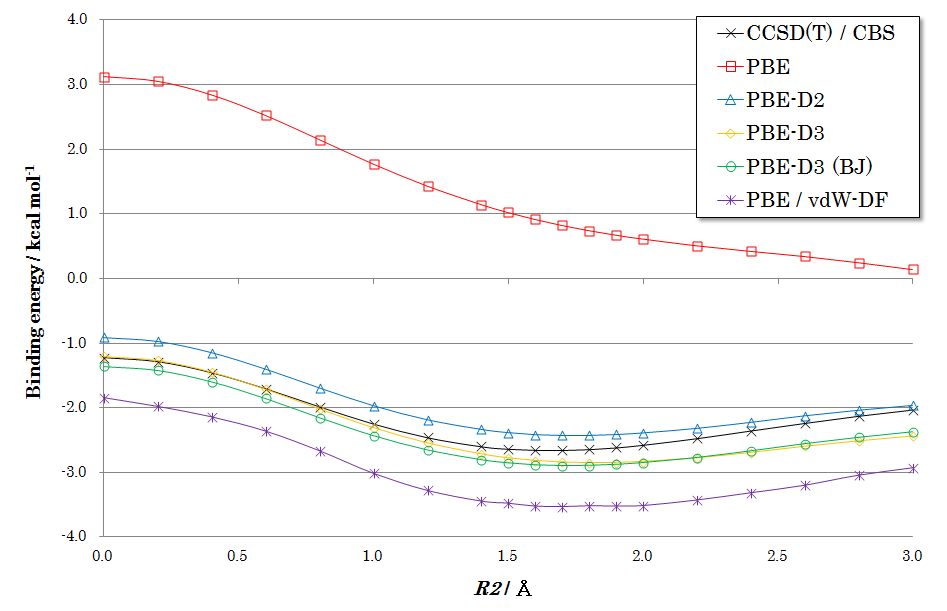
図4.　Parallel-Displaced型ベンゼン二量体のポテンシャル曲面

応用事例：多層グラフェン#

次に、DFT-D法を層状物質へ適用した事例として、多層グラフェンの層間距離の最適化計算結果を示します。

図5.　2層および3層グラフェンのモデル。

表1と表2に、各種計算手法による2層および3層グラフェンの最適化された層間距離を示します。

PBE（補正なし）: 分散力相互作用を考慮しないPBEでは、層間距離が他の手法に比べてかなり大きな値となり、層間の引力を過小評価していることがわかります。
DFT-DとvdW-DF: DFT-D補正を加えた手法（PBE-D2, PBE-D3, PBE-D3(BJ)）は、高コストな1-shot vdW-DFの結果と近い値を与えます。
精度の比較: 特にPBE-D3は、2層グラフェエン（3.17 Å）、3層グラフェン（3.11 Å）ともに、1-shot vdW-DFの結果（それぞれ約3.18 Å、約3.11 Å）と極めてよく一致しており、層状物質の構造予測においても非常に有効であることが示されました。

表1.　2層グラフェンの層間距離（Å）

手法	PBE	PBE-D2	PBE-D3	PBE-D3(BJ)	1-shot vdW-DF
層間距離 (Å)	3.40	2.91	3.17	3.04	3.18

表2.　3層グラフェンの層間距離（Å）

手法	PBE	PBE-D2	PBE-D3	PBE-D3(BJ)	1-shot vdW-DF
層間距離 (Å)	3.24	2.91	3.11	3.01	3.11

まとめ#

本稿では、第一原理計算ソフトウェアAdvance/PHASEを用い、DFT-D法がファンデルワールス相互作用を記述するための効率的かつ高精度な手法であることを2つの事例を通して示しました。具体的には、ベンゼン二量体の計算ではDFT-D法（特にDFT-D3およびD3(BJ)）が高精度なCCSD(T)計算に匹敵するポテンシャルエネルギー曲面を再現できることを確認し、多層グラフェンの構造最適化においても高コストなvdW-DF法と同等の結果を低コストで与えられることを実証しました。これらの結果から、DFT-D法は分子間相互作用やナノ材料科学分野における大規模系の構造探索や動力学シミュレーションにおいて、信頼性と計算効率のバランスがとれた非常に有望な手法であると言えます。

参考文献#

DFT-D2: S. Grimme, J. Comput. Chem. 27, 1787 (2006).
DFT-D3: S. Grimme, J. Antony, S. Ehrlich, H. Krieg, J. Chem. Phys. 132, 154104 (2010).
DFT-D3(BJ): S. Grimme, S. Ehrlich, L. Goerigk, J. Comput. Chem. 32, 1456 (2011).