帯電した点欠陥の形成エネルギー補正計算の解析事例 (FNV法 & eFNV法)#

PHASE logo

半導体や絶縁体中の点欠陥は、材料の電気的・光学的特性に決定的な影響を与えます。第一原理計算は、これらの点欠陥の性質を原子レベルで解明する強力なツールです。特に、欠陥が電荷を帯びている場合、その形成エネルギーはフェルミ準位に依存し、材料のキャリア濃度や伝導型を左右します。しかし、計算手法に由来する有限サイズ効果は、帯電欠陥系のエネルギーを正しく評価する上で深刻な問題となります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的な半導体であるガリウムヒ素（GaAs）中の帯電欠陥を例に、この有限サイズ効果を補正する標準的な手法であるFNV法と、それを拡張したeFNV法の利用方法と得られた結果について解説します。

Keywords: 第一原理計算, 点欠陥, 形成エネルギー, 有限サイズ効果, FNV法, extended FNV法, GaAs

理論的背景：なぜ補正が必要か？#

電荷 $q$ を持つ欠陥の形成エネルギー $E_f[D^q]$ は、次式で与えられます [1]。

$E_f[D^q] = \{E[D^q] + E_\text{corr}[D^q]\} - E_P - \sum_i n_i \mu_i + q(\epsilon_{VBM} + \Delta\epsilon_f)$

ここで、 $E[D^q]$ は欠陥を含むスーパーセルの全エネルギー、 $E_P$ は完全結晶の全エネルギー、 $E_\text{corr}[D^q]$ が本稿の主題である有限サイズ効果の補正エネルギーです。スーパーセル法を用いた計算では、欠陥を含むセルを周期的にもうけますが、これにより本来は孤立しているべき欠陥の「コピー（周期イメージ）」が生まれ、非物理的な静電相互作用が生じます。また、計算セル全体の電荷を中性に保つために人為的に導入される背景電荷も誤差の原因となります。これらの人為的な効果を取り除き、無限に大きい結晶中の孤立した単一欠陥のエネルギーを得るために、 $E_\text{corr}[D^q]$ の計算が不可欠です。

FNV法#

FNV法 [2] は、この有限サイズ補正の標準的な手法です。補正エネルギーは、主に2つの項からなります。

$E_\text{corr}^{FNV} = E_{l} - q\Delta V$

長距離静電相互作用の補正 ( $E_{l}$ ): 欠陥電荷の周期イメージ間のクーロン相互作用を補正する項です。第一原理計算で得られた欠陥周りの電荷分布をガウス関数などのモデルで近似し、そのモデル電荷の周期的配列のエネルギーから、孤立したモデル電荷のエネルギーを差し引くことで計算されます。
ポテンシャル・アライメント補正 ( $q\Delta V$ ): 帯電欠陥と背景電荷により、欠陥セルの静電ポテンシャルは完全結晶のポテンシャルからずれてしまいます。このズレを補正するため、欠陥から遠く離れた領域で、欠陥セルのポテンシャルとモデルポテンシャルの差 $\Delta V$ を計算し、ポテンシャルの基準を揃えます。

Extended FNV (eFNV) 法#

FNV法は等方的な誘電体を持つ材料では有効ですが、層状物質など方向によって誘電率が異なる異方性材料では精度が低下します。eFNV法は、この点を改良した手法です [3, 4]。

異方性誘電テンソルの考慮: eFNV法では、スカラー量としての誘電率の代わりに、誘電率テンソルを用いて静電相互作用を計算するため、より現実的な材料に対応できます。
原子サイトポテンシャルによるアライメント: FNV法がセルのグリッド上の静電ポテンシャルを用いるのに対し、eFNV法は各原子サイトの静電ポテンシャルを利用してアライメントを行います。これにより、原子の構造緩和が大きい系や低対称性の系でも、より信頼性の高い補正が可能です。

Advance/PHASEによる計算手順#

ここでは、GaAs中のGaサイトに電荷q=-3の空孔 (X) を導入したモデルの計算手順を示します。図1に計算モデル（2x2x2スーパーセル使用）を示します。構造最適化の結果、欠陥周囲の原子が完全結晶とは異なる位置に配置されることがわかります。

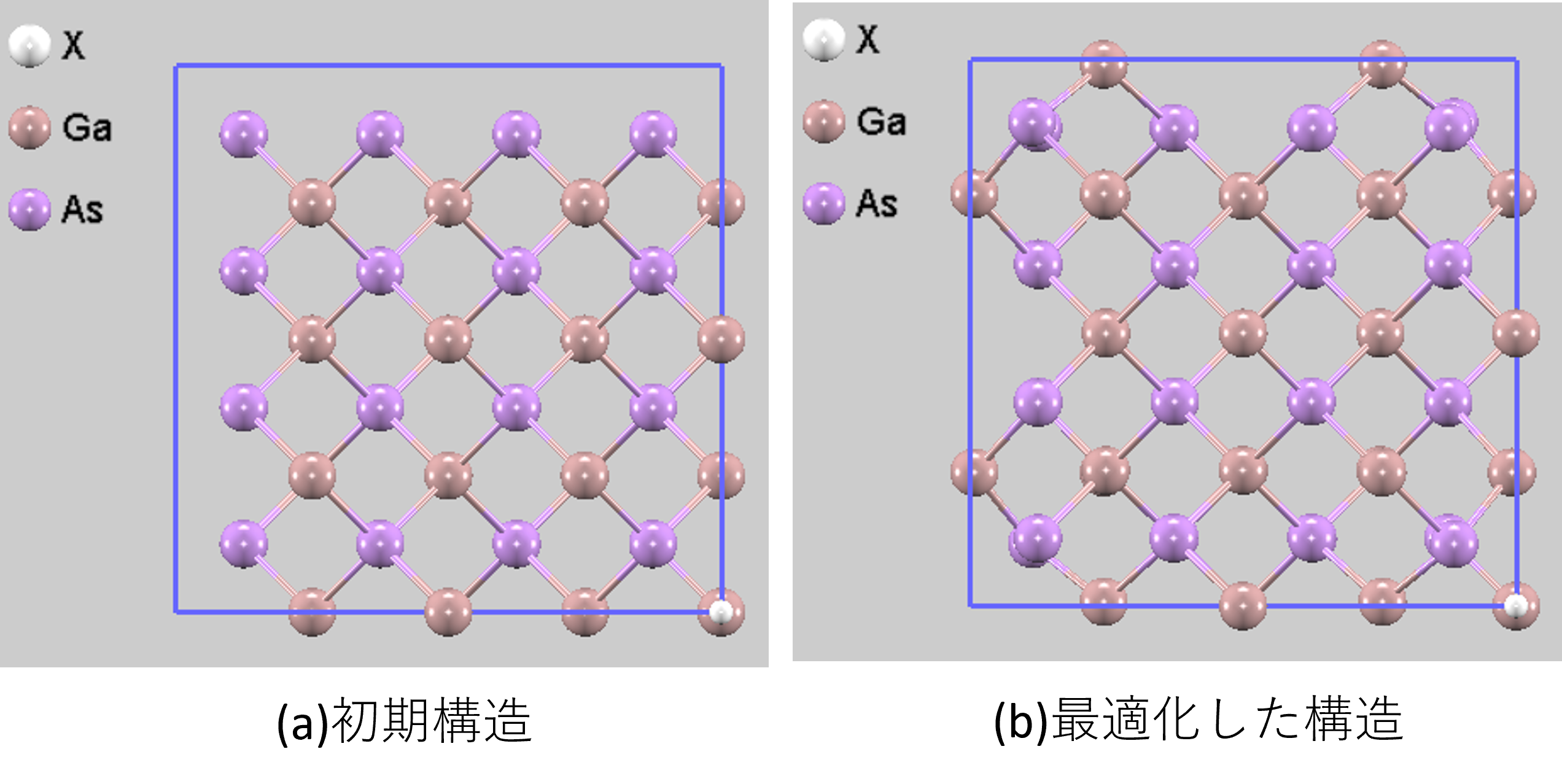
計算モデル

図1.　Ga欠陥１個を含むGaAs(2x2x2)計算モデル。Xは空孔の位置を示しています。

Advance/PHASEでは、FNV法が実装されたpymatgen-analysis-defects [5]、eFNV法が実装されたpydefect [6] が同梱されており、それぞれ連携して利用することが可能です。補正計算は、大きく分けて2つのステップで実行します。(1) 完全結晶（バルク）と帯電欠陥を含む系それぞれについて自己無撞着計算（SCF計算）を行い、静電ポテンシャルを出力します。 (2) 出力されたポテンシャルファイルを用いて、ポスト処理としてAdvance/PHASEのGUIから補正計算を実行します。

静電ポテンシャルの出力設定#

補正手法に応じて、必要なポテンシャルファイルの形式を選択します。

FNV法: cube形式を選択します。これにより、セルのグリッド上の静電ポテンシャルデータが es_potential.cube ファイルに出力されます。
Extended FNV法: at_core形式を選択します。これにより、各原子サイトの静電ポテンシャルデータが es_potential_at_core.dataファイルに出力されます。

補正計算の実行#

計算結果処理におけるcharged defect correction機能を選択し、手法（FNVまたはextended FNV）に応じて設定を行います。

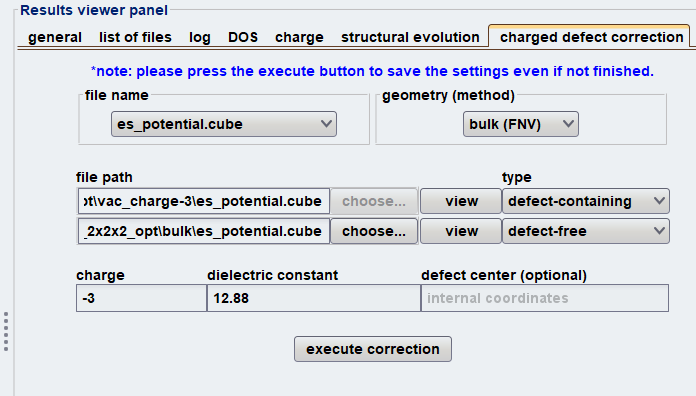FNV法による補正計算のGUI設定図2.　FNV法の補正計算設定画面。欠陥系と完全結晶のcubeファイル、電荷、誘電率を入力します。

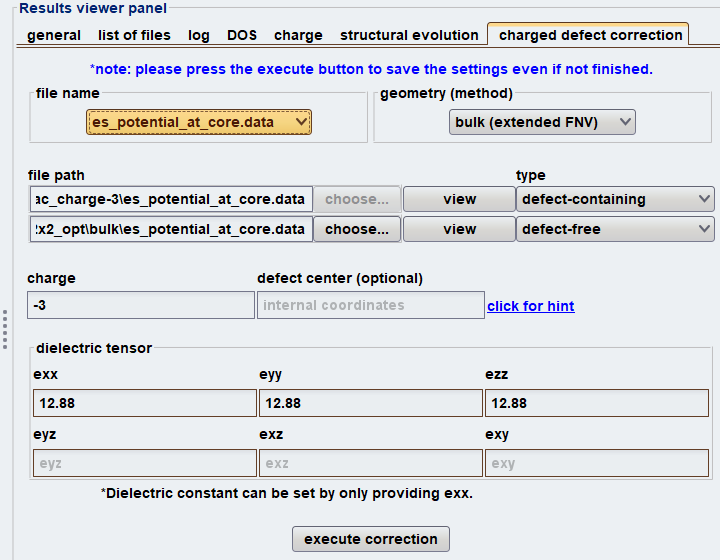Extended FNV法による補正計算のGUI設定図3.　eFNV法の補正計算設定画面。at_core.dataファイル、電荷、誘電テンソルを入力します。

計算結果と考察 (GaAs, q=-3)#

ここでは、GaAs中のGa欠陥（電荷q=-3）モデルの計算結果を示します。

FNV法による結果#

図4は、スーパーセルの各格子ベクトル方向（direction 0, 1, 2）について、FNV法のポテンシャル・アライメントの様子を示したグラフです。グラフにおいて、赤線（DFT locpot diff）は、欠陥セルと完全結晶セルの生の静電ポテンシャルの差を表しており、周期的な振動が見られます。黒線（long range from model）は、FNV法で仮定したモデル電荷が作る長距離的なポテンシャルです。緑線（short range）は、赤線から黒線の効果を差し引いたもので、欠陥から離れた領域（sampling region）でほぼゼロになるようにアライメントされます。この時のシフト量がアライメント補正値 $\Delta V$ となります。

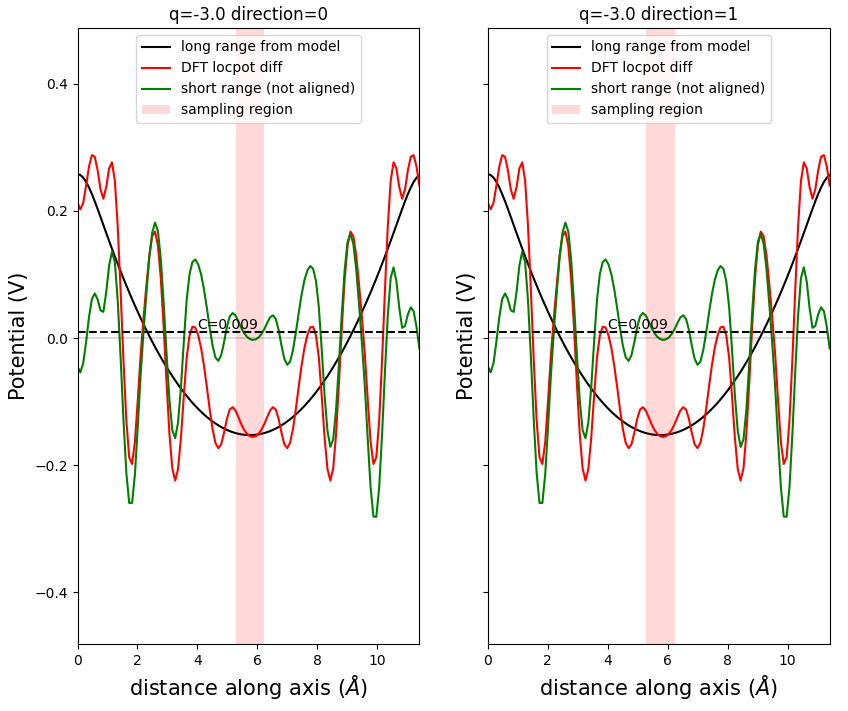FNV法によるポテンシャルアライメントプロット図4. FNV法によるポテンシャル・アライメントの結果 (q=-3)。direction=2の結果は省略しています。

FNV法による最終的な補正エネルギーは、ログファイルに出力され、1.213 eV となりました。

Extended FNV法による結果#

eFNV法では、原子サイトの静電ポテンシャルを用いてアライメントを行います。計算結果の詳細はログファイルに出力されます。各原子サイトでのポテンシャル差（vdef-vref）、モデルポテンシャル（pc_potential）、そして両者の差（potential_difference）がリストされます。最終的な補正エネルギーは 1.216 eV と計算されました。

両手法の比較#

今回の計算対象であるGaAsは立方晶であり、等方的な誘電体とみなせます。このような系では、両手法の結果は良く一致することが期待されます。表1に両手法から得られた補正エネルギーの内訳を示します。

表1.　FNV法とeFNV法による補正エネルギーの比較 (GaAs, q=-3)

補正項	FNV法 (eV)	eFNV法 (eV)
Point Charge Correction	1.2406	1.2412
Alignment Correction	-0.0276	-0.0248
Total Defect Correction	1.2130	1.2164

表1が示すように、両手法による合計補正エネルギーは非常によく一致しており、その差はわずか0.003 eVです。これは、等方性材料に対する両手法の整合性の高さを示すものです。一方で、異方性の強い材料を扱う場合は、誘電テンソルと原子サイトポテンシャルを適切に扱えるeFNV法がより信頼性の高い結果を与えます [3]。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、帯電した点欠陥の形成エネルギーにおける有限サイズ効果の補正計算を行いました。GUIを用いた簡単な設定で、標準的なFNV法と、より汎用性の高いeFNV法の両方を実行できることを示しました。GaAsの帯電空孔の例では、両手法が非常によく一致した結果を与えることを確認しました。欠陥物性を正確に予測するためには、このような補正計算が不可欠となります。

参考文献#

熊谷悠, "半導体点欠陥の第一原理計算", まてりあ 55, 221 (2016).
C. Freysoldt, J. Neugebauer, and C. G. Van de Walle, "Fully Ab Initio Approach to Point-Defect Energies", Physical Review Letters 102, 016402 (2009).
Y. Kumagai, and F. Oba, "Electrostatics and first-principles calculations of charged defects in semiconductor supercells", Physical Review B 89, 195205 (2014).
Y. Kumagai, N. Tsunoda, A. Takahashi, and F. Oba, "Insights into oxygen vacancies from high-throughput first-principles calculations", Phys. Rev. Materials 5, 123803 (2021).
https://github.com/materialsproject/pymatgen-analysis-defects
https://github.com/kumagai-group/pydefect