Si結晶中のドナー準位の高精度な第一原理計算: 数千原子のモデルを用いた解析例#

PHASE logo

半導体技術において、シリコン(Si)などの半導体に不純物（ドーパント）を添加し、その電気的特性を制御することは極めて重要です。特に、リン(P)やヒ素(As)のようなV族元素をドナーとして添加すると、結晶内に余剰電子が供給され、伝導帯のすぐ下に「ドナー準位」と呼ばれる新たなエネルギー準位が形成されます。このドナー準位のエネルギー（束縛エネルギー）は、半導体のキャリア濃度や導電性を決定づける基本的な物理量です。本稿では、このドナー準位を高い精度で決定するため、第一原理計算ソフトウェアAdvance/PHASEを用いたシミュレーションを実施しました。特に、数千原子規模に達する計算モデルを用いることで、計算上の人為的な影響を排し、実験値に迫る高精度な計算を実現します。ここでは、Si中にドープされたAs原子がつくるドナー準位の計算を例に、そのアプローチと結果を詳述します。

Keywords: 第一原理計算, ドナー準位, シリコン, 不純物ドーピング, 半導体, スーパーセル法, 有効質量近似, 密度汎関数法(DFT)

計算手法と解析モデル#

半導体中の不純物準位を理解するアプローチとして、最もシンプルで古典的な理論モデルとして有効質量近似（EMA）が広く用いられてきました [1]。この手法は、電子が結晶中の有効質量を持った粒子として振る舞うと仮定する簡便なモデルですが、不純物原子周辺の局所的なポテンシャルの乱れや格子歪みの効果を精密に扱うことは困難です。これに対し、本解析で用いる第一原理計算（密度汎関数法, DFT）とスーパーセル法は、原子レベルの詳細な電子状態を量子力学に基づいて直接解くことで、より現実に即した高精度な解析を可能にします。

スーパーセル法は、結晶中に不純物を一つ配置した単位格子（スーパーセル）を考え、それを周期的に繰り返すことで不純物を含む結晶全体をモデル化する手法です。しかし、この手法では計算モデルの周期性から、不純物とその周期イメージ（隣のセルにある不純物）との間に意図しない相互作用が生じ、計算結果に影響を与える可能性があります。特に、ドナー電子のように空間的に広がった波動関数を持つ場合、この相互作用は無視できません。この問題を克服し、真に孤立した不純物の状態を模擬するためには、スーパーセルのサイズを十分に大きくして、不純物間の距離を離す必要があります。

本解析では、このスーパーセルサイズ依存性を系統的に評価するため、Si原子216個から8000個までの様々なサイズのスーパーセルを用意し、中心のSi原子を1つだけAs原子に置き換えたモデル（図1）を作成しました。このような数千原子規模の大規模な第一原理計算は、膨大な計算資源を必要とします。本解析は、地球シミュレータをはじめとするスーパーコンピューティング環境を活用することで実行可能となりました。

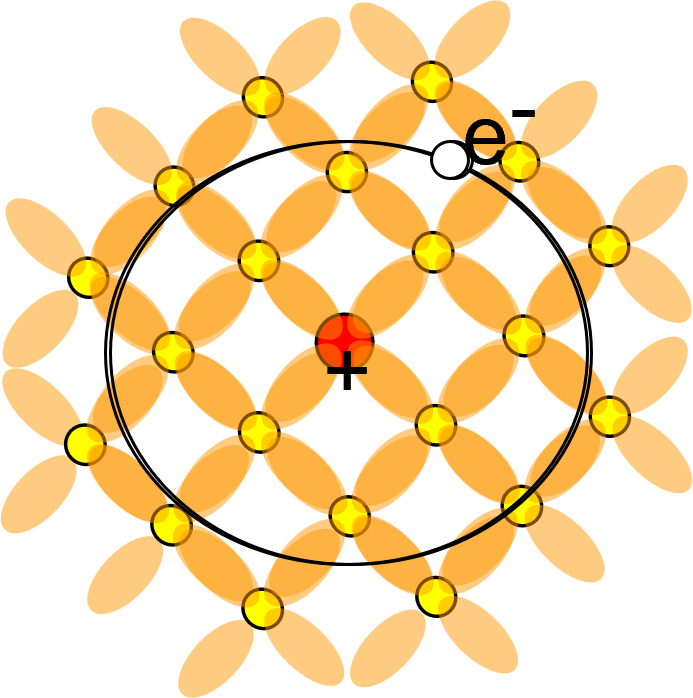
Si中のAs置換モデル

図1. Siスーパーセル中のAs置換不純物モデルの模式図
シリコン結晶の共有結合ネットワークの中心にあるSi原子（黄色）を、一つだけV族のAs原子（赤色）で置き換えたモデル。AsはSiより価電子が一つ多いため、余剰電子（e⁻）が結晶に供給され、これがドナー電子として振る舞います。

計算結果と考察#

ドナー電子の波動関数#

図2は、ドナー状態に対応する電子の波動関数を可視化したものです。この図は、ドナー電子がどのように結晶内に存在しているかを理解する上で重要です。

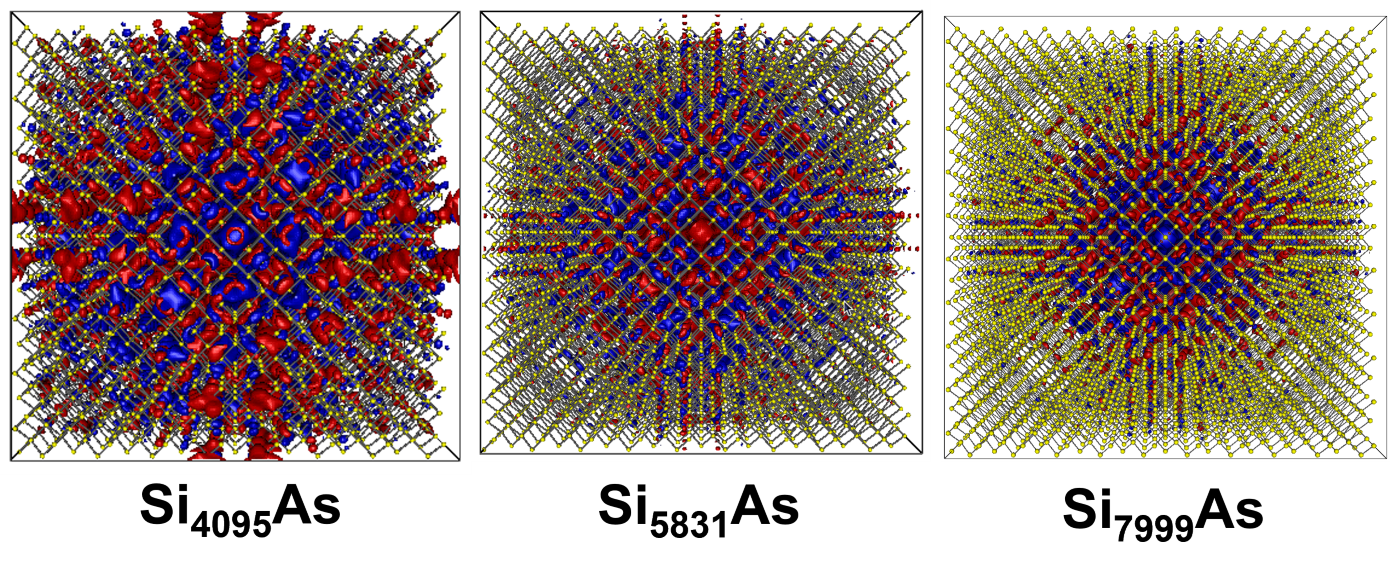
ドナー電子の波動関数

図2. Si中のAsドナー電子の波動関数の等値面。赤と青は波動関数の正負の位相を表します。
スーパーセルのサイズをSi₄₀₉₅As、Si₅₈₃₁As、Si₇₉₉₉Asと大きくした場合の比較。As原子（中心）に束縛されながらも、波動関数が非常に広く分布している様子がわかります。計算の高精度を達成するためには、この波動関数の広がりを十分に内包できる大規模なモデルが必要となります。

ドナー電子は、As原子核のクーロン引力によって束縛され、原子核周辺に局在しています。しかし、その波動関数は非常に大きく空間的に広がっており、多くのSi原子にまたがっていることがわかります。この「波動関数の広がり」こそが、スーパーセル法で高精度な計算を行う上での鍵となります。計算に用いるスーパーセルがこの広がりよりも小さいと、電子は隣のセルの原子（周期イメージ）と人工的に相互作用してしまうので、この広がりを完全に内包できるほど大きなセルが高精度な計算に必要となるのです。

ドナー準位エネルギーのスーパーセルサイズ依存性#

図3は、各スーパーセルサイズについて計算されたドナー準位の束縛エネルギーを、セルの大きさに対してプロットしたものです。

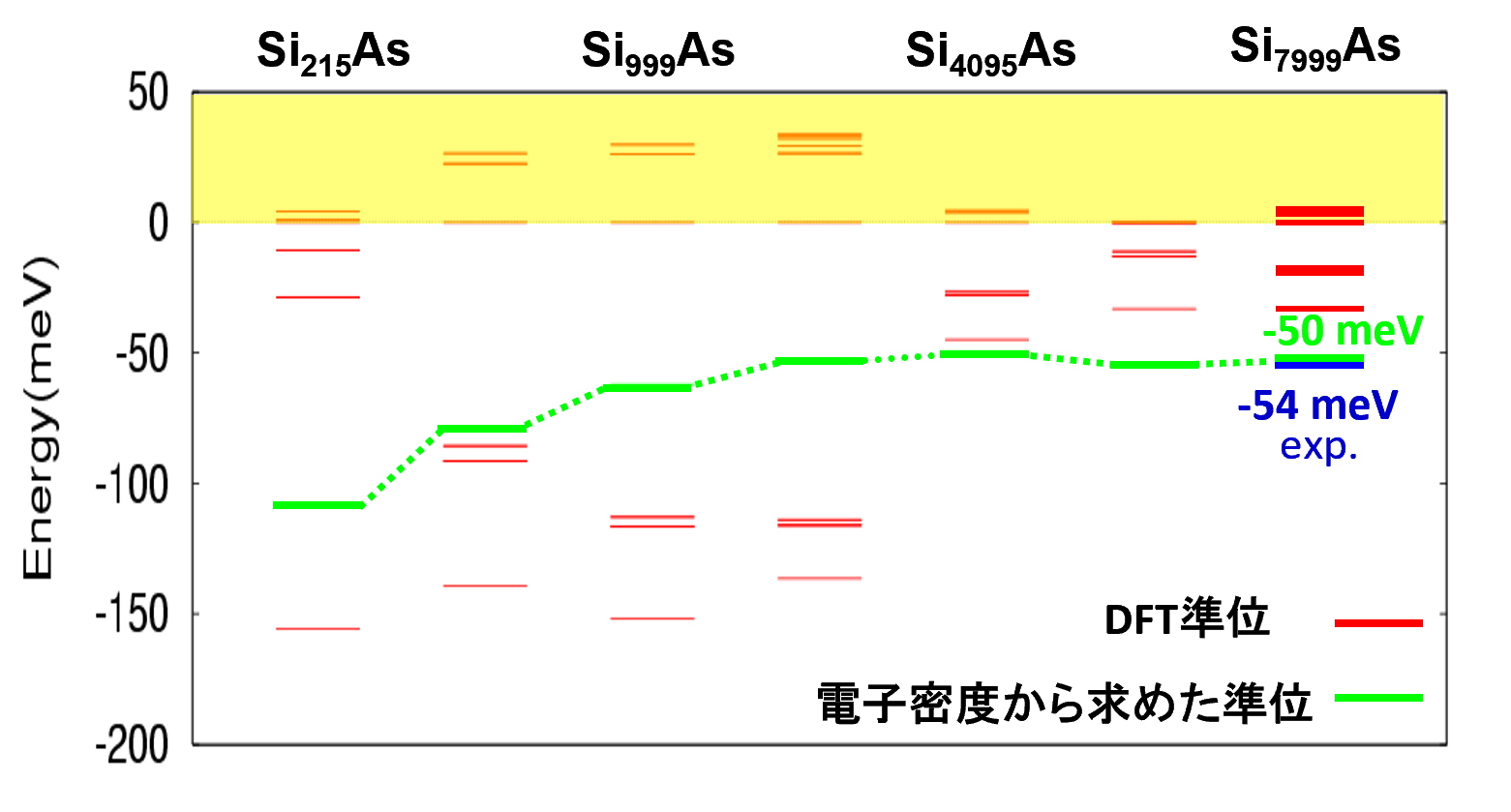
ドナー準位のスーパーセルサイズ依存性

図3. Asドナー準位の束縛エネルギーのスーパーセルサイズ依存性
横軸に各スーパーセルモデル、縦軸にエネルギー（伝導帯の底を0 eVとする）を示します。赤線はDFT計算から直接得られる準位（DFT準位）、緑線は電子密度から求めたドナー準位を表します。

「電子密度から求めた準位」の計算手法について

グラフの緑線で示された「電子密度から求めた準位」は、DFT計算の結果と有効質量理論の物理モデルを組み合わせた、より高度な解析手法によって算出されています。具体的には、以下のような手順に基づいています。

まず、DFT計算によって、ドナー原子の個性を反映したリアルなドナー電子の分布（波動関数 $\psi(r)$ ）を正確に求めます。
次に、その電子の存在確率 $\left|\psi(r)\right|^2$ の空間的な広がりを、有効質量理論における水素原子様波動関数の理論的な形（1s軌道の場合、 $|\psi(r)|^2 \propto e^{-2r/a_B^*}$ という指数関数的な形）にフィッティングします。
このフィッティングにより、DFT計算が捉えたリアルな電子の広がりを最もよく再現する軌道半径、すなわち有効ボーア半径 ( $a_B^*$ )を抽出します。
最後に、この有効ボーア半径を有効質量理論のエネルギー公式に代入することで、スーパーセルのサイズ効果が補正された、精度の高いドナー準位（緑線）を算出するのです。

このグラフは、ドナー準位の計算値がスーパーセルのサイズにどう依存するかを示しています。特に、緑線で示された「電子密度から求めた準位」に注目すると、セルサイズが小さいモデル（グラフ左側の Si₂₁₅As など）では、ドナー準位は、本来あるべき値よりも深く（より大きな負の値に）なっています。セルサイズが大きくなると、準位は次第に浅い方（0 meVに近い方）へと変化します。そして、Si₄₀₉₅As を超える大規模なモデルでは、準位がほぼ一定の値に収束していることが見て取れます。特に、Si₇₉₉₉Asで得られた約-50 meVという値は、文献 [2] で報告されている実験値と極めてよく一致しており、本計算手法の精度の高さを示しています。

ドナー電子のポテンシャルエネルギー分布#

ドナー準位エネルギーの収束性をより詳細に評価するため、ドナー電子のポテンシャルエネルギー分布(Potential density contribution, PED)を解析しました（図4）。これは、As原子から各距離にある電子が、そのポテンシャルエネルギーにどれだけ寄与しているかを示すものです。

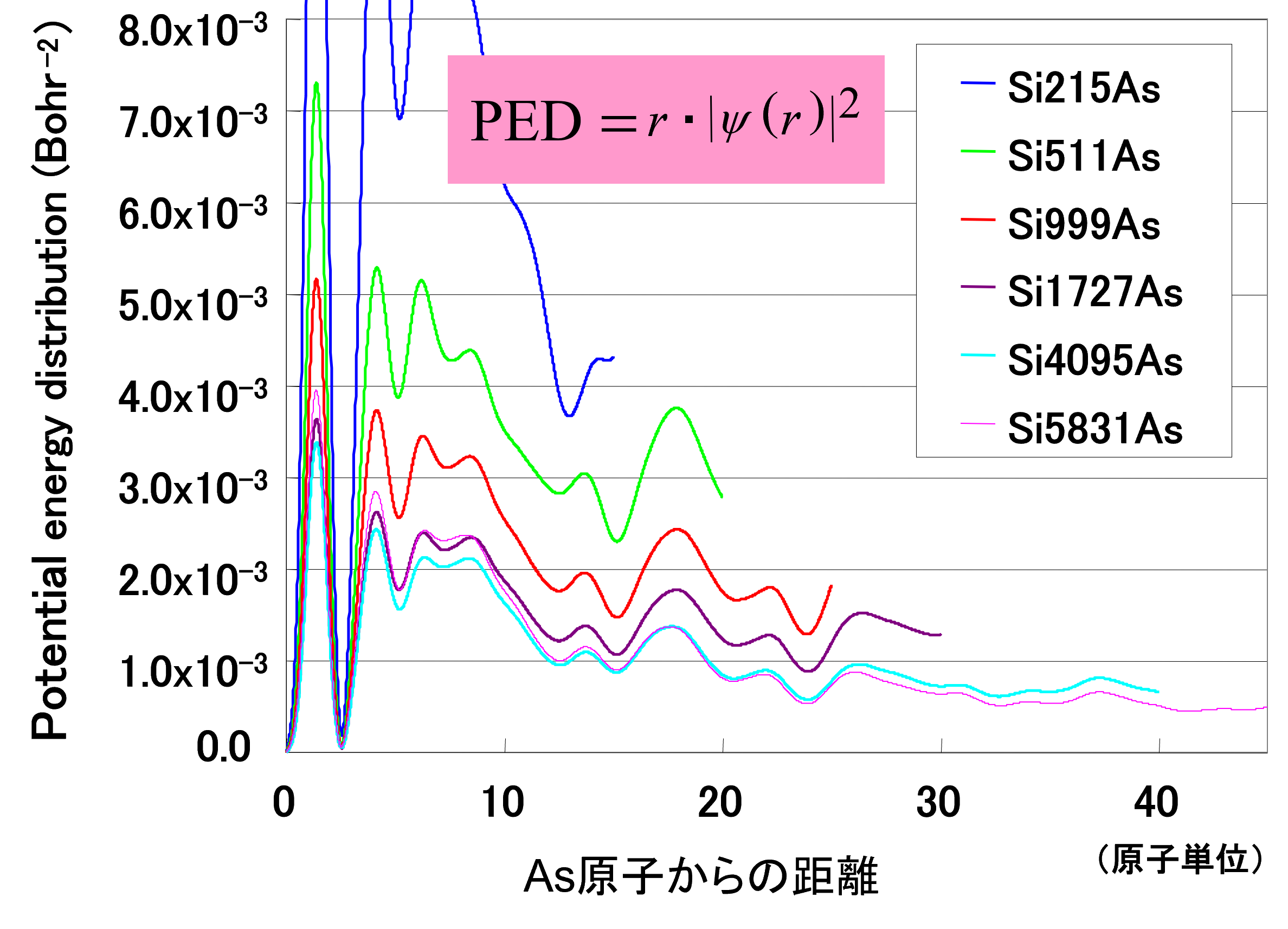
ドナー電子のポテンシャルエネルギー分布

図4. Asドナー電子のポテンシャルエネルギー分布（PED）
ドナー電子の波動関数|ψ(r)|²に距離rを乗じた分布で、As原子から各距離における電子の存在確率を視覚化している。セルサイズが小さいモデル（青線：Si₂₁₅Asなど）では、隣接セルとの人工的な相互作用により分布が大きく振動する。一方、4000原子を超える大規模モデル（水色・ピンク線）では分布の形がほぼ一致しており、計算結果がセルサイズに対して十分に収束し、孤立したドナーの状態を正確に再現できていることを示しています。

セルサイズが小さい場合（青線：Si₂₁₅As）、分布は大きく振動しており、隣接セルとの人工的な相互作用が強く影響していることが分かります。一方、セルサイズを大きくするにつれて分布は安定し、4000原子を超えるモデル（水色・ピンク線）では、２つの結果がほぼ重なっています。これは、計算結果がセルサイズに対して十分に収束し、孤立したドナーの状態を正しくシミュレートできていることを視覚的に裏付けるものです。

考察：計算規模と精度の関係

今回の解析結果は、第一原理計算における計算モデルの規模と、得られる結果の精度の関係を考える上で重要な示唆を与えます。

～数百原子レベルの計算の位置づけ: この規模のモデルは、第一原理計算では標準的かつ実用的なアプローチです。以下のような物理現象の定性的な理解から定量的な評価に非常に有効です。
- 傾向の把握: ドーピングによってバンドギャップ内に準位が形成されるか、その準位が浅いか深いかといった基本的な性質を理解できます。
- 相対比較: 複数の不純物候補がある場合に、どちらがよりデバイス特性に適しているかなど、候補間の優劣を比較検討するのに役立ちます。
- 局所構造の解析: 不純物周りの原子がどのように歪むかといった、局所的な構造変化を調べるのに適しています。
今回の計算の意義: 一方で、本解析のように数千原子規模のモデルを用いた計算は、実験値と数meV程度の誤差というレベルの高精度なドナー準位を得ることを可能にします。このようにして得られた高精度な結果は、～数百原子レベルの計算で捉えられた物理モデル（ドナー電子の束縛など）が正しかったことを裏付ける役割も果たします。つまり、小規模な計算で物理を理解し、大規模な計算でその正しさを精確に証明するという、相補的な関係が成り立ちます。今回の成果は、第一原理計算がスーパーコンピュータの能力を引き出すことで、現実の材料の特性をいかに精確に予測できるかを示した先進的な事例です。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、Si中のAsドナー準位のエネルギーをスーパーセル法により高精度に解析しました。数千原子を含むスーパーセルモデルを用いることで、ドナー電子の広がった波動関数に起因する人工的な相互作用を排し、孤立したドナーの状態を忠実にシミュレートしました。その結果、計算から得られたドナー準位は、実験値と極めて良好な一致を示しました。これは、第一原理計算が半導体中の不純物準位のような繊細な物理現象を、実験に匹敵する精度で予測できることを実証するものです。本研究のような高精度計算は、半導体デバイスの特性を原子レベルから理解・設計するための強力な指針となります。

参考文献#

P. Y. Yu and M. Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Springer (1996).
R. L. Aggarwal and A. K. Ramdas, "Optical determination of the symmetry of the ground states of group-V donors in silicon", Phys. Rev. 140, A1246 (1965).