結晶中の自己格子間原子の拡散障壁の評価#

半導体デバイスの製造プロセスや信頼性において、結晶欠陥の挙動を理解することは極めて重要です。特に、シリコン(Si)結晶中に存在する自己格子間原子(self-interstitial)は、ドーパントの異常拡散などを引き起こす原因となり、デバイス特性に大きな影響を与えます。この格子間原子が結晶中をどのように移動(拡散)するのか、そのメカニズムとエネルギー障壁を定量的に評価することは、製造プロセスの最適化や信頼性向上に不可欠です。本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装されたNEB(Nudged Elastic Band)法を用い、Si結晶中における自己格子間原子の拡散過程をシミュレーションし、その拡散障壁エネルギーを評価します。
Keywords: 第一原理計算, DFTシミュレーション, NEB法, 拡散障壁, 自己格子間原子, シリコン(Si), 欠陥拡散
計算手法#
原子や分子が化学反応や拡散を起こす際、初期状態から最終状態へ移行するまでには、エネルギー的に最も有利な特定の経路(最小エネルギー経路)をたどります。この経路上でエネルギーが最も高くなる点が遷移状態であり、そのエネルギーと始状態のエネルギーの差が活性化エネルギー(拡散障壁)となります。
本解析では、このような拡散経路とエネルギー障壁を特定するために、NEB(Nudged Elastic Band)法 [1] を用います。NEB法は、始状態と終状態の原子配置の間に、反応経路を表現するための中間状態(レプリカ)を複数配置し、それらを仮想的なバネでつない「バンド」として扱います。このバンド全体のエネルギーが最小になるように各レプリカの原子位置を最適化することで、最小エネルギー経路と遷移状態を効率的に探索することができます。
さらに、本解析では遷移状態をより正確に特定するため、CI-NEB(Climbing Image NEB)法 [2] を適用しました。これは、NEB計算で得られた反応経路上のエネルギーが最も高いレプリカ(遷移状態に最も近い状態)を特定し、そのレプリカにのみ経路に沿ってエネルギーが最大化する方向の力を働かせる手法です。通常のNEB法では、レプリカがエネルギーの鞍点を通り過ぎてしまうことがありますが、CI-NEB法ではこの「クライミング(登攀)」動作により、レプリカが真の鞍点(遷移状態)へと正確に収束します。これにより、計算コストを過度に増やすことなく、拡散障壁エネルギーを高い精度で決定することが可能になります。
計算モデル#
拡散過程と結晶構造#
本解析で想定する拡散過程は、格子間位置(interstitial)に存在するSi原子が、隣接する結晶格子点のSi原子を押し出し、その原子が新たな格子間原子となって移動する、いわゆる「間接的な原子の入れ替わり」によるメカニズムです。
計算モデルとして、65個のSi原子を含む3次元周期境界条件下のスーパーセルを用いました。本解析で設定した拡散の始状態(図1左)と終状態(図1右)は、構造最適化で決められた二つの安定構造です。両者のエネルギーの差はわずか0.0056 eVです。
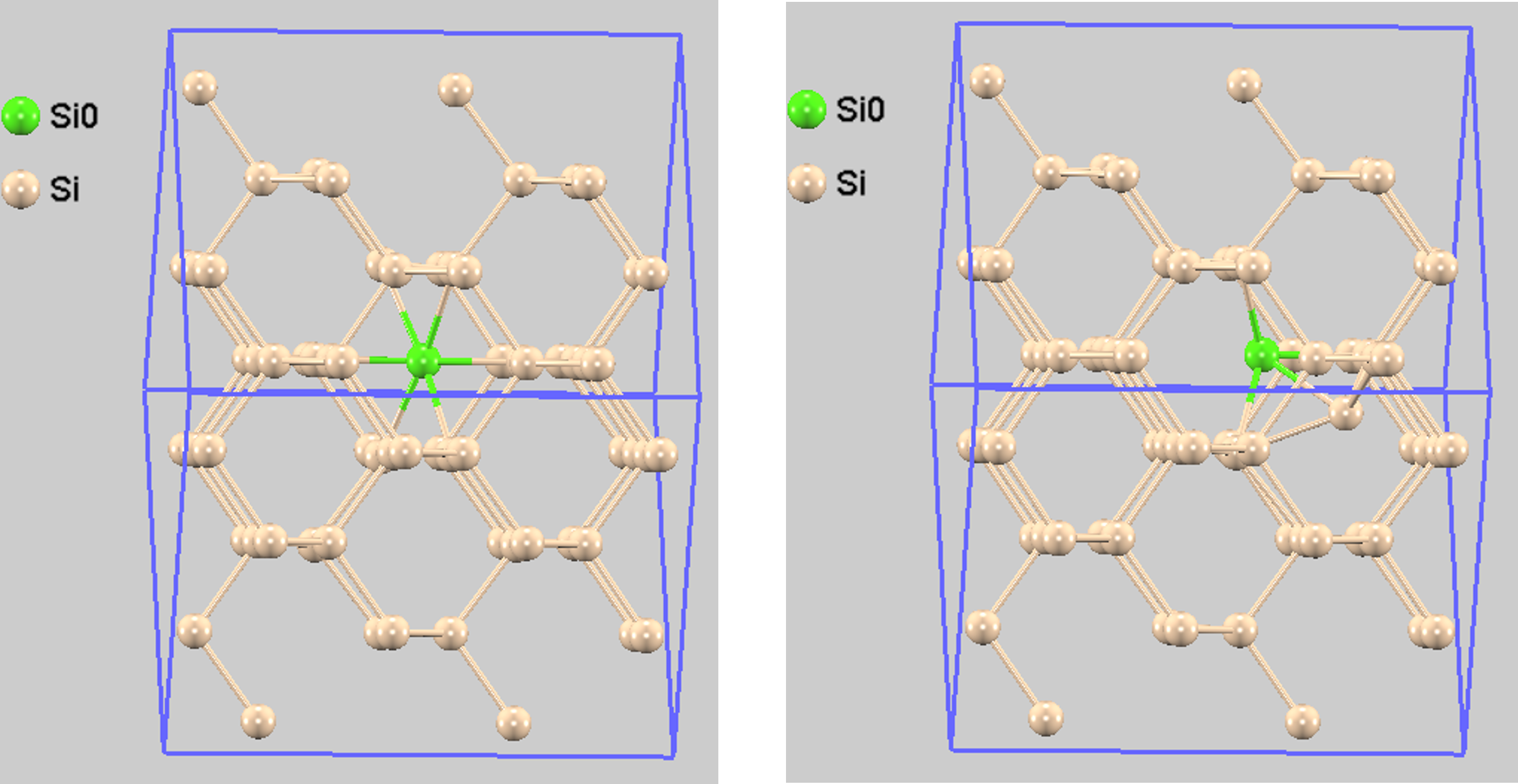
図1. 拡散の始状態(左)と終状態(右)の計算モデル。肌色は通常のSi原子、緑色は拡散する格子間原子を表します。
計算条件#
詳細な計算設定は表1の通りです。カットオフエネルギーは系内に存在する最も「硬い」原子に応じて設定されますが、本モデルはSi原子のみで構成されているため、比較的低いカットオフエネルギー でも計算が可能であることが知られています。
表1. 主な計算条件
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ノルム保存擬ポテンシャル |
| 交換相関汎関数 | GGA-PBE |
| カットオフエネルギー | 16 Rydberg |
| k点サンプリング | Γ点のみ |
| NEBレプリカ数 | 8(両端を除く) |
計算結果と考察#
NEB計算(FIRE最適化アルゴリズム使用、 65回で収束)によって得られた、Si自己格子間原子の拡散経路に沿ったエネルギー変化を図2に示します。横軸は反応座標(始状態から終状態までの経路上の位置)、縦軸は始状態を基準とした相対エネルギーを表します。
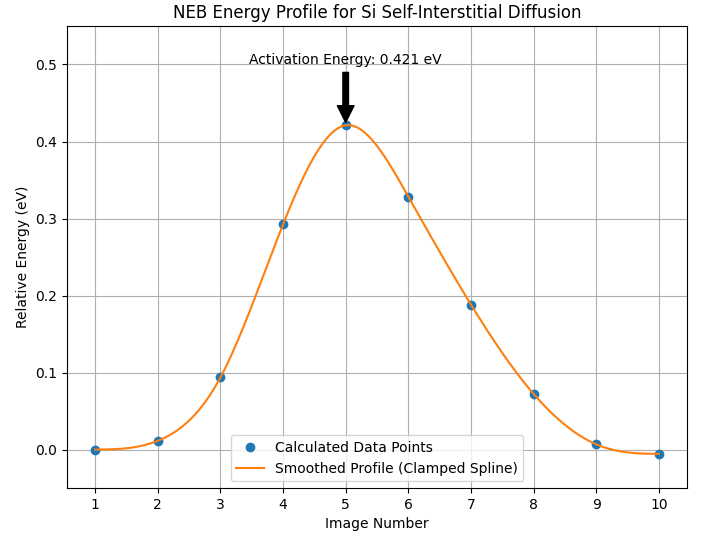
図2. 拡散経路に沿ったエネルギー変化
この結果から、本拡散過程におけるエネルギー障壁(活性化エネルギー)は約0.42 eVであることが分かりました。始状態から終状態へ向かう過程で、中間に一つのエネルギーの山を持つ、比較的単純な反応経路であることが確認できます。この0.42 eVという値は、格子間原子がSi結晶中を移動するために乗り越える必要のあるエネルギーの大きさを定量的に示したものです。
図3に、エネルギーが最も高くなる遷移状態(エネルギー障壁の頂点)での原子配置を示します。この拡散は、自己格子間原子が単に格子間を飛び移るのではなく、格子上の原子を「蹴り出す」ようにして間接的に拡散していくダイナミックな過程です。このような過程で遷移状態の構造を具体的に特定できることは、拡散メカニズムを原子レベルで深く理解する上で非常に有益です。
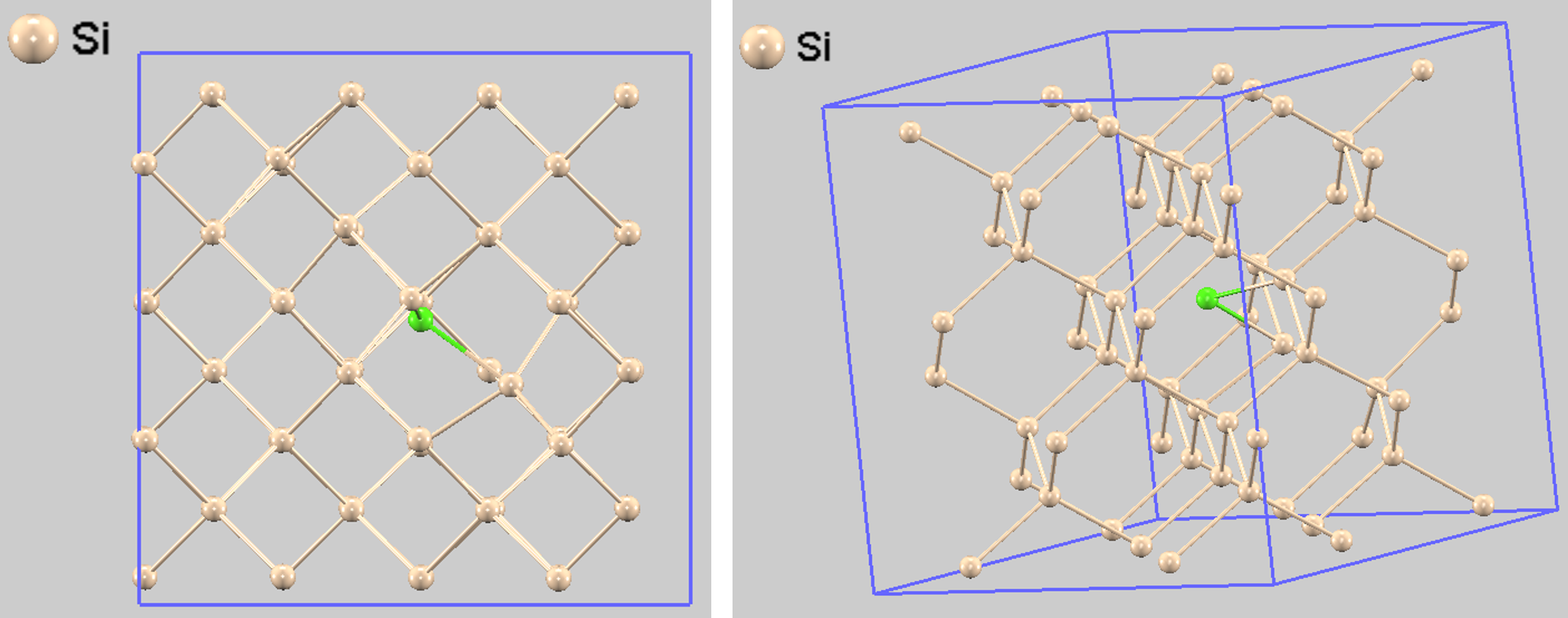
図3. 遷移状態(エネルギー障壁の頂点)での原子配置: (左) front view (右) perspective view
本計算で得られた拡散障壁0.42 eVという値は、過去の理論研究と比較しても非常に興味深い結果です。Si結晶中に中性の自己格子間原子の安定サイトと移動経路は、計算手法や用いるポテンシャルによって見解が分かれています。特に、文献 [3] では、静的なDFT計算(GGA)で拡散障壁が0.20 eVと報告され、その後の第一原理分子動力学 (MD) 計算 [4] では拡散障壁が0.45 eVが報告されています。本計算でNEB法/CI-NEB法を用いて得られた結果は、この第一原理MDの解析結果に非常に近いことが示されています。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、NEB/CI-NEBでSi結晶中の自己格子間原子の拡散過程をシミュレーションしました。その結果、格子間原子が隣接原子を押し出して移動するメカニズムにおける拡散障壁が約0.42 eVであることを定量的に評価しました。この値は、先行研究の結果と整合的であり、Si中の中性自己格子間原子の熱的な拡散を支配する基本的なエネルギー障壁として妥当なものであると考えられます。このような計算は、半導体中の欠陥ダイナミクスを解明し、より信頼性の高いデバイス開発に貢献する重要な知見となります。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- G. Henkelman and H. Jónsson, "Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points", J. Chem. Phys. 113, 9978 (2000).
- G. Henkelman, B. P. Uberuaga, and H. Jónsson, "A climbing image nudged elastic band method for finding saddle points and minimum energy paths", J. Chem. Phys. 113, 9901 (2000).
- W. K. Leung, R. J.Needs, G. Rajagopal, S. Itoh, S. Ihara, "Calculations of silicon self-interstitial defects", Phys. Rev. Lett. 83, 2351 (1999).
- B. Sahli, W. Fichtner, "Ab initio molecular dynamics simulation of self-interstitial diffusion in silicon", Phys. Rev. B 72, 245210 (2005).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学