原子置換によるグラフェンの強磁性の誘起#

グラフェンは、炭素原子が蜂の巣状に結合したシート状の二次元物質であり、その特異な電子的・機械的特性から、次世代のエレクトロニクス材料として注目されています。しかし、本来のグラフェンは非磁性であるため、スピントロニクスデバイスなど磁性を利用した応用には限界がありました。この課題を克服するアプローチの一つが、グラフェンの一部を他の原子で置き換える「原子置換ドーピング」です。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、グラフェンの炭素原子をマンガン(Mn)原子で置換した際の電子状態と磁気特性をシミュレーションし、強磁性が誘起されるメカニズムを明らかにします。
Keywords: 第一原理計算, DFTシミュレーション, グラフェン, 原子置換, 強磁性, スピントロニクス, バンド構造, 状態密度, GGA+U
計算モデルと計算条件#
本解析では、置換を行わない純粋なグラフェンと、炭素原子の1つをMn原子で置換したモデル(Mn置換グラフェン)の2種類を対象としました(図1)。
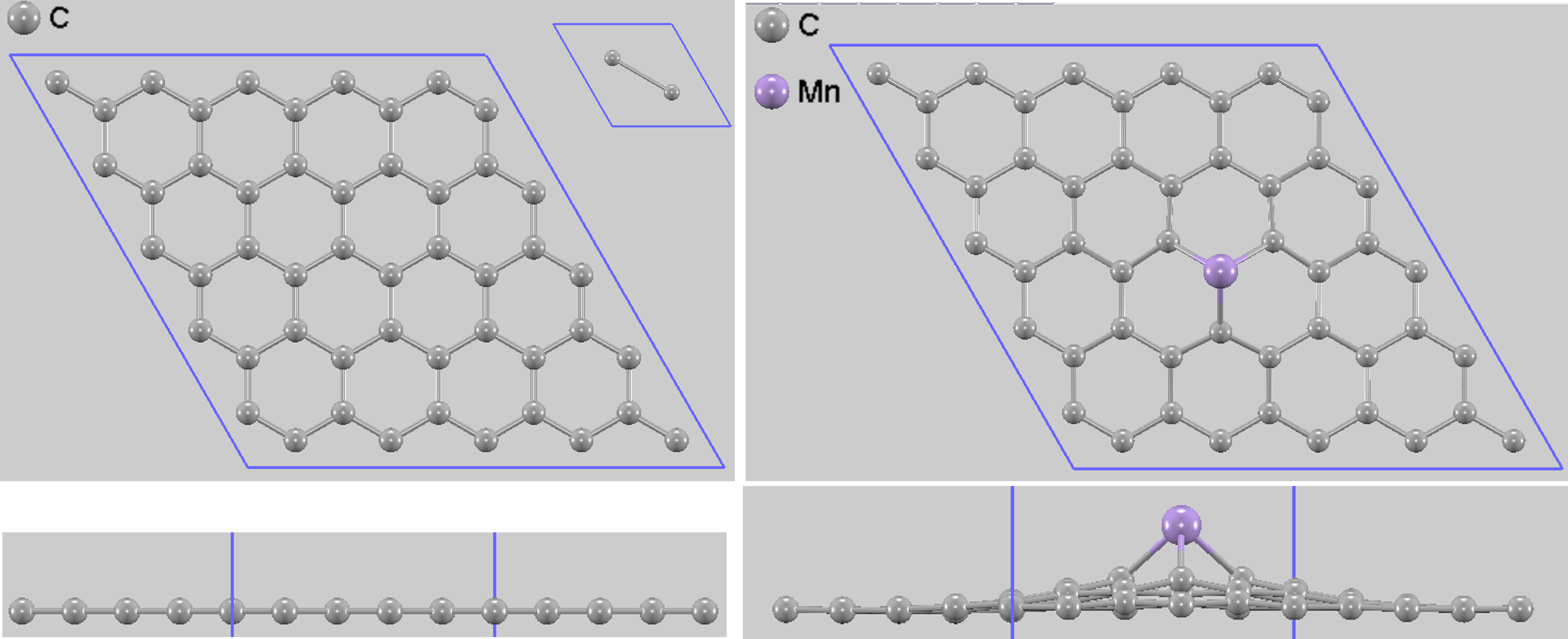
図1. 5x5 pure graphene (左)とMn置換5x5 graphene(右)の上面図と側面図。左辺の上にあるインセットに純粋なグラフェンの基本単位格子を示しています。
純粋なグラフェンでは、2原子単位格子に対してセル最適化を行い、格子定数として 2.4564 Å を得ました(C-C距離:1.42 Å)。この際、2つの炭素原子の分数座標は、データベースなどで見られる0.33333のような近似値ではなく、十分な桁数を取って(2/3, 1/3, 0), (1/3, 2/3, 0) になるように正確に表現される必要があります。次に、この最適化された単位格子を用いて5x5のスーパーセル(合計50原子サイト)を作成し、中央の炭素原子を一つMn原子に置き換えました。 構造最適化の結果、Mn原子はグラフェン平面から垂直方向に変位し、安定化します。GGAを用いた計算では、Mn原子はグラフェン平面の上、約1.39 Åの高さに位置する構造が最も安定となります 。この時、Mn原子と最も近い3つの炭素原子との結合距離は1.83 Åです 。
電子状態計算は、密度汎関数法(DFT)に基づき、以下の条件で行いました。GGA+U計算において、Uの値は文献 [1] を参照し、Mn原子の3d軌道に適用しました。
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル |
| 交換相関汎関数 | GGA (PBE), GGA+U (U = 5.39 eV) |
| 波動関数のカットオフエネルギー | 25 Rydberg |
| k点サンプリング (SCF) | グラフェン: 24x24x1 Mn置換グラフェン: 5x5x1 |
| 構造最適化の収束閾値 | 2.0 x 10-4 Hartree/bohr |
計算結果と考察#
純粋なグラフェンの電子状態#
まず基準として、グラフェンの基本単位格子を使用して、純粋なグラフェンの電子状態を計算しました。図2のバンド構造では、フェルミ準位(エネルギー0 eV)付近のK点で価電子帯と伝導帯が点接触しており、グラフェン特有の「ディラックコーン」が形成されていることが確認できます。また、図3の状態密度(DOS)からも、フェルミ準位での状態密度がゼロであり、グラフェンがゼロギャップ半導体であることが示されています。
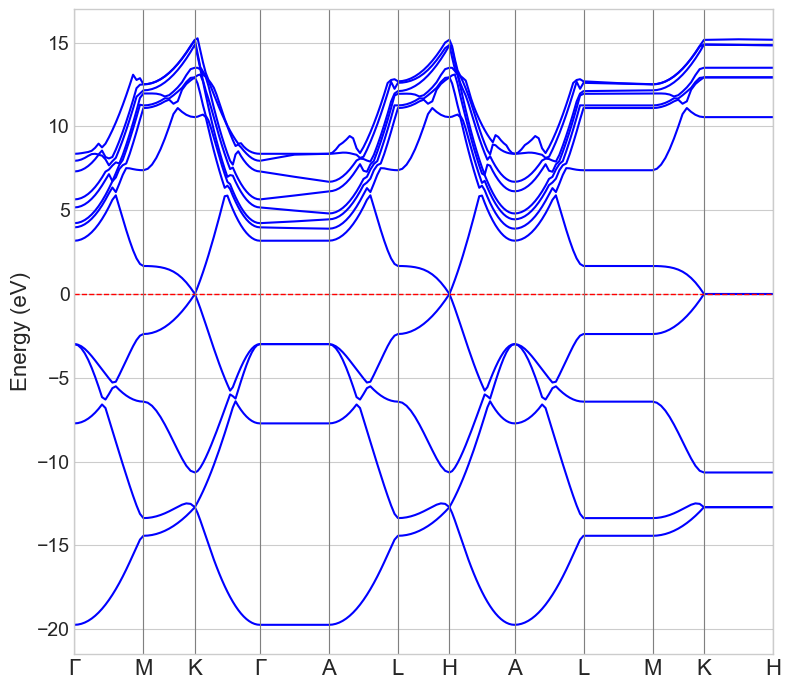
図2. 純粋なグラフェンのバンド構造。赤の点線はフェルミ準位を示しています。
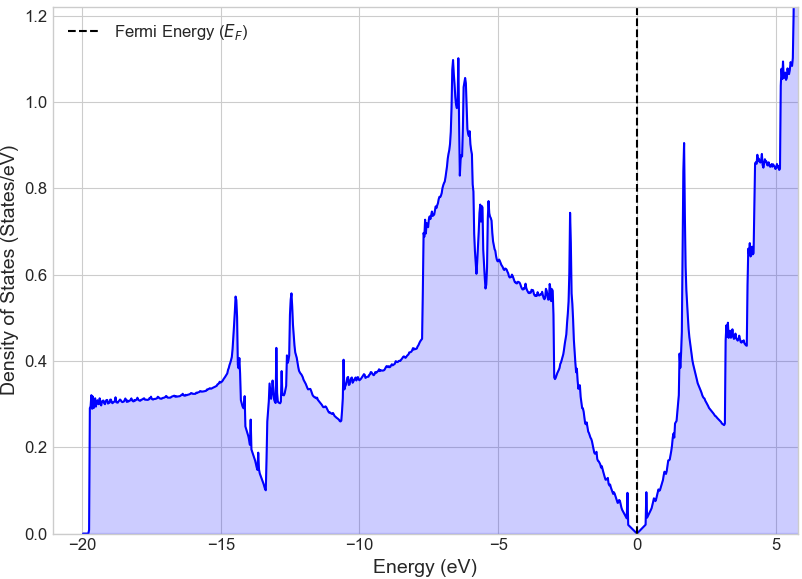
図3. 純粋なグラフェンの状態密度。フェルミ準位において状態密度が厳密にゼロであり、ゼロギャップ半導体であることを示しています。これはバンド構造のディラックコーンと一致します。状態密度がフェルミ準位近傍で線形に増加するV字型の形状は、グラフェンが持つ優れた電気的特性の根源です [2]。
Mn置換グラフェンの電子状態と磁性#
次に、Mnを置換したグラフェンの電子状態を解析しました。図4は、一般化勾配近似(GGA)を用いて計算した状態密度です。上半分がスピンアップ、下半分がスピンダウンの状態密度を表します。スピンアップとダウンの分布が非対称になっており、系がスピン分極して磁性を帯びていることがわかります。また、フェルミ準位 に注目すると、スピンダウンの状態が有限の値を持ち金属的な性質を示す一方で、スピンアップの状態はギャップが開いており半導体的な性質を示します。この結果、物質全体としてはハーフメタル的な振る舞いを示すことが示唆されます。
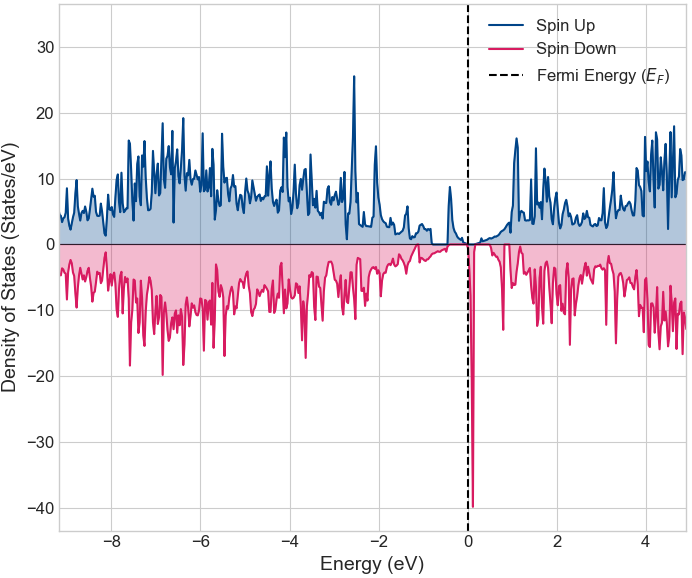
図4. Mn置換グラフェンの状態密度 (GGA)。正・負の値はスピンの向き(アップ・ダウン)を示しています。
遷移金属であるMnのd軌道電子は、電子間の反発(電子相関)が強く、GGAではその効果を十分に記述できない場合があります。そこで、電子相関の効果を取り入れるGGA+U法を用いて計算を行いました。その結果、図5に示すようにフェルミ準位に明確なバンドギャップが形成され、半導体的な性質に変化しました。
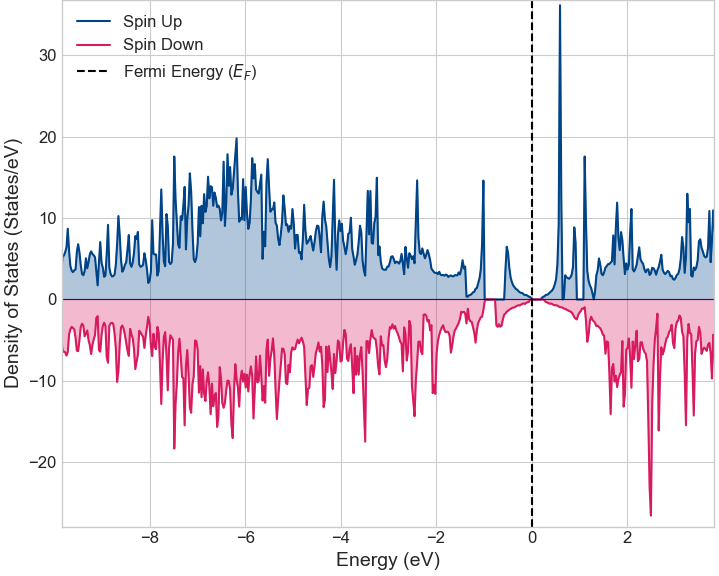
図5. Mn置換グラフェンの状態密度 (GGA+U)。正・負の値はスピンの向き(アップ・ダウン)を示しています。
図6にGGA+U法によるバンド構造を示します。青線がスピンアップ、赤線がスピンダウンのバンドを表しており、両者が大きく分離していることから、スピン縮退が解けて強磁性状態になっていることがわかります。フェルミ準位を跨ぐ形で約0.18 eVのバンドギャップが形成されており、価電子帯の頂上と伝導帯の底が同じ波数ベクトル(K点)に位置する直接遷移型の半導体であることが示されました。このバンドギャップの値は、参考文献の報告値(約0.2 eV)と良い一致を示しています。
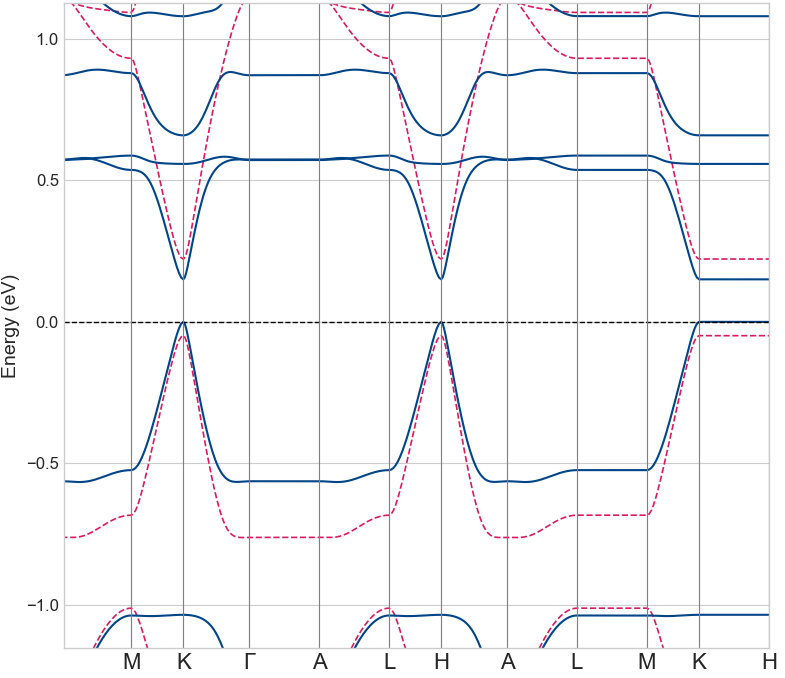
図6. Mn置換グラフェンのバンド構造 (GGA+U)
磁性の強さを示す磁気モーメントアップはスピンとダウンスピンの電子数の差から計算しました。GGAとGGA+Uのどちらの手法でも、Mn原子あたり3.0 μBという大きな値が得られました。
この系全体の合計磁気モーメントが 3.0 μBという整数値になることは、理想的なイオンモデルで考えると、Mn原子が実効的に3個の不対電子を持つ状態に対応します。中性Mn原子([Ar] 3d5 4s2)は炭素の役割を模倣するため、グラフェンが持つ2種類の結合(σ結合とπ結合)に対応する必要があります。まず、周囲の炭素原子3つと平面的な骨格を成す「σ結合」を形成するために3つの価電子を使います。さらに、グラフェンの電気的特性を担う「π結合系」を安定させるために、もう1つの価電子を供給します。このように合計4つの価電子が結合に使われた結果、Mn原子は+4価に近い電子状態([Ar] 3d3)となり、結合に関与しない残りの3つのd電子が、スピンを揃えた不対電子として留まります。これが、観測された磁気モーメントの直接的な起源です。GGAとGGA+Uの双方で同じ整数値が得られたことは、この磁気状態が非常に安定的で明確に定義されていることを示しています。ただし、この局在したd電子のエネルギー準位を正確に記述するには電子相関の考慮(GGA+U)が不可欠であり、それが系を半金属から半導体へと正しく描写する鍵となります。
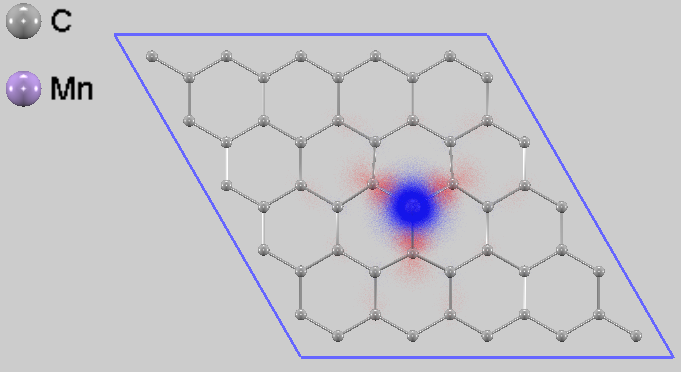
図7. Mn置換グラフェンのスピン密度分布
図7にスピン密度分布を示します。これはスピンアップ電子密度とスピンダウン電子密度の差分を可視化したものであり、磁性の源泉が空間的にどのように分布しているかを示します。Mn原子上には、正のスピン分極(図中の青い領域)が強く局在しており、これが大きな磁気モーメントの主な要因であることを示しています。興味深いことに、その周囲に位置する最近接の炭素原子上には、逆向きの負のスピン分極(図中の赤い領域)が誘起されています。この結果は、Mn原子とその周囲の炭素原子との間に反強磁性的な相互作用が存在することを示唆しています。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いてMn原子を置換したグラフェンの電子状態と磁性を評価しました。Mn原子の置換により、本来非磁性であるグラフェンに強磁性が誘起され、Mn原子あたり3.0 μBという大きな磁気モーメントが発現することが明らかになりました。また、電子相関を考慮したGGA+U計算により、Mn置換グラフェンは約0.18 eVのバンドギャップを持つ直接遷移型の半導体となることが示されました。これらの結果は、原子置換ドーピングがグラフェンのような二次元材料の物性を劇的に変化させ、新たな機能性を付与するための有効な手段であることを示しており、第一原理計算がこのような材料設計において強力な予測ツールとなることを実証しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- M. Wu, C. Cao, and J. Z. Jiang, “Electronic structure of substitutionally Mn-doped graphene”, New Journal of Physics 12, 063020 (2010).
- A. H. Castro Neto, F. Guinea, N. M. Peres, K. S. Novoselov, and A. K. Geim, "The electronic properties of graphene", Rev. Mod. Phys. 81, 109 (2009).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学