ドーパント原子同士の相互作用を解き明かす:第一原理計算による安定構造予測#

半導体デバイスの電気特性は、材料中に注入されたドーパント(不純物原子)の分布に極めて敏感です。しかし、微小領域に存在する微量なドーパントの分布を実験的に正確に測定することは非常に困難です。第一原理計算は、物質の電子状態に基づいて原子レベルでの安定構造を予測できるため、ドーパント分布を評価する上で非常に有効な手法となります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、シリコン(Si)結晶中に注入された各種ドーパント原子(B, P, As)が、エネルギー的にどのような配置で安定化するのかを明らかにします。
Keywords: 第一原理計算, DFTシミュレーション, ドーパント分布, Si, スーパーセル法, 構造最適化, B, P, As
計算モデルと計算条件#
Si結晶中のドーパント分布をシミュレートするため、スーパーセル法を用いました。まず、Siのユニットセル(基本繰り返し単位、図1左)を3×3×3に拡張したスーパーセル(図1右)を構築します。このスーパーセルは216個のSi原子を含みます。
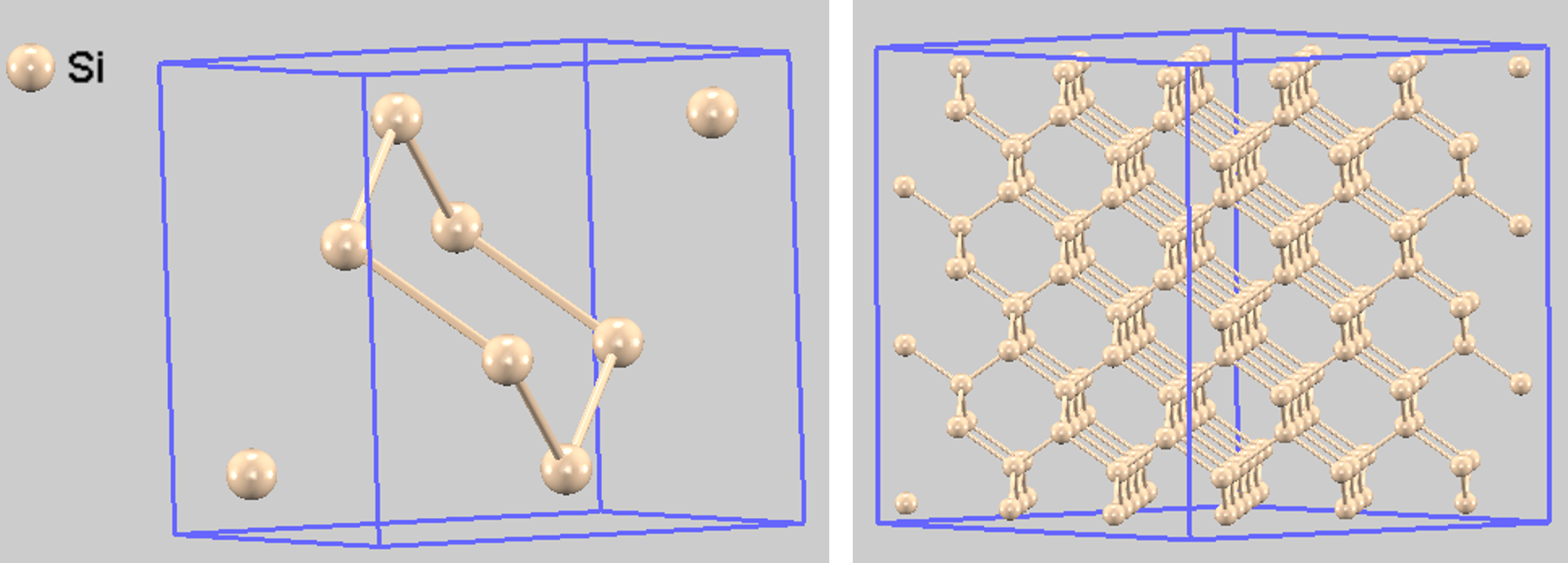
図1. (左) Si結晶のユニットセル、(右) 計算に用いた3×3×3スーパーセル。
次に、このスーパーセル内にドーパント原子を2個配置します。本解析では、特にアニール初期過程などで見られる格子間原子のクラスタリング挙動に注目するため、ドーパント原子はSi原子と置き換わるのではなく、格子間サイトへの配置を仮定します。原子同士が近すぎないよう、Si原子との距離が共有結合半径の和以上となる位置(図2の①~⑤)を初期配置の候補としました。
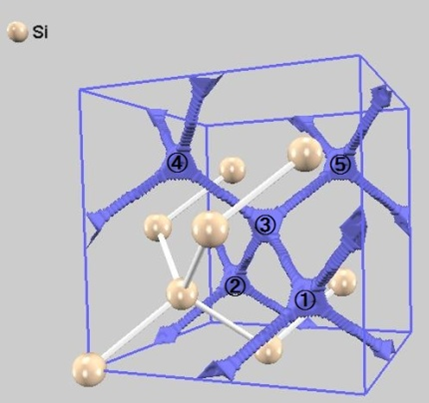
図2. Si結晶格子内のドーパント原子が侵入可能な隙間(①~⑤)。
様々なドーパント原子間距離を網羅的に評価するため、スーパーセル内でのユニットセルの組み合わせを3パターン(タイプA, B, C)用意し、さらにその中のサイト(①~⑤)の組み合わせを変えることで、多数の初期構造を作成しました。この3パターンは、2つ配置するドーパント原子の初期距離を系統的に変えるための分類です。広範囲な原子間相互作用を網羅的に評価するため、以下のように初期配置を分けています。
- タイプA: 2つのドーパントを近距離に配置するパターン。原子同士が結合(クラスタ化)するような短い距離での安定性を調べます。
- タイプB: 2つのドーパントを中距離に配置するパターン。
- タイプC: 2つのドーパントを遠距離に配置するパターン。スーパーセル内で可能な限り離し、孤立した状態での安定性を調べます。
これらの初期構造について、原子に働く力が一定のしきい値以下になるまで構造を最適化し、全エネルギーを比較します。ただし、ここで重要なのは同じ元素内での配置の違いによるエネルギーの相対的な変化です。元素が異になるとエネルギーの基準値そのものが異なるため、例えばBとPでエネルギーの絶対値を比較することに物理的な意味はありません。
本解析で用いた主な計算条件の例(ドーパントがBの場合)は表1に示されています。
表1. 計算条件の概要 (Bドーパントの例)
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル (Si: ノルム保存) |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数カットオフエネルギー | 25 Rydberg |
| k点サンプリング | Γ点 |
| 構造最適化の収束条件 | 原子に働く力の最大値 < 1.0e-04 Hartree/Bohr |
計算結果と考察#
Si中のB (ホウ素) ドーパント分布#
様々な初期配置から構造最適化を行った結果を、最終的なB原子間の距離と系の全エネルギーの関係としてプロットしたのが図3です。エネルギーが低いほど、その構造が安定であることを意味します。
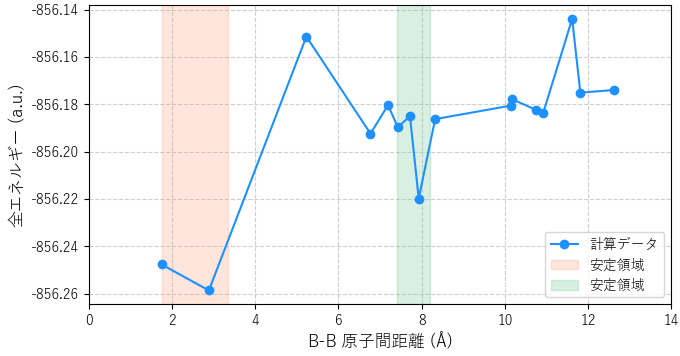
図3. Bドーパントの原子間距離と全エネルギーの関係。
図3から、Bドーパントの安定な配置には2つの領域があることが分かります。一つは原子間距離が2~3 Åの領域で、もう一つは8 Å付近の領域です。これは、B原子が互いに引き合って結合を形成する(クラスタ化する)か、あるいはある程度離れて孤立した状態で安定化することを示唆しています。この結果は、シリコン中のボロンの挙動に関する多くの理論的研究 [1, 2] とよく一致しています。図4に、それぞれの領域に対応する代表的な安定化構造を示します。
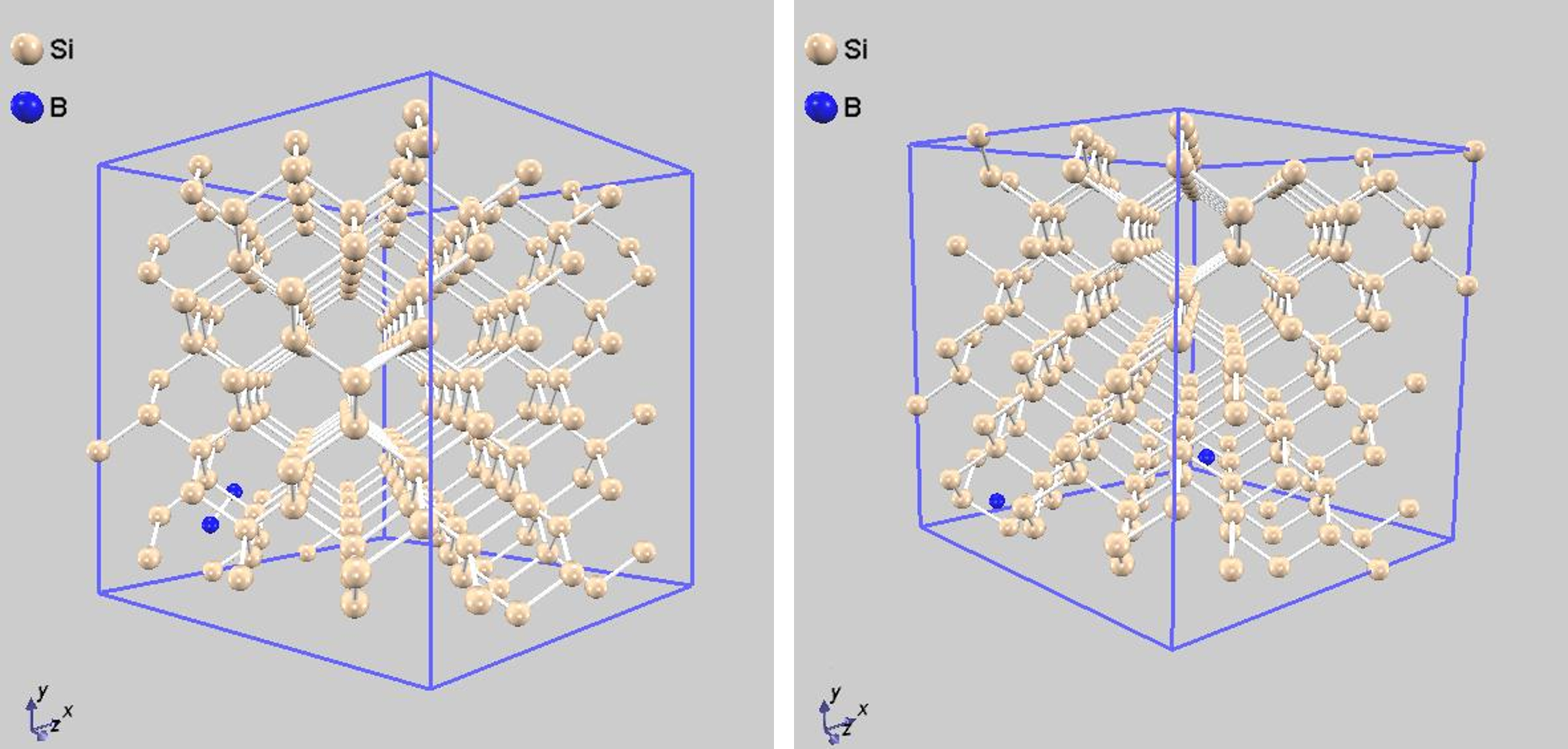
図4. Bドーパントの安定化構造の例。(左)2つのB原子が結合した状態。(右)2つのB原子が離れて孤立した状態。
Si中のP(リン), As(ヒ素)のドーパント分布#
同様の計算をP, Asについても行いました。図5に各ドーパントのエネルギー分布を示します。
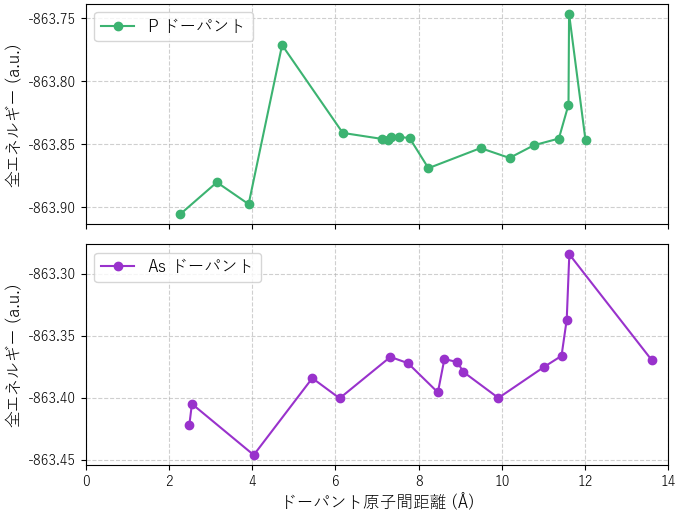
図5. (上から) P, Asのドーパント原子間距離と全エネルギーの関係。
- P (リン): Bと同様に、原子間距離が2~4 Åの近距離と、8 Å付近の遠距離に安定な領域が見られます。図6(左)のように、P原子がSi原子と結合を形成することで安定化します。
- As (ヒ素): 原子間距離が約4 Å付近の領域で最も安定化しました。図6(右)のように、As原子がSi原子と結合を形成することで安定化します。しかし、原子間が離れるとエネルギーが増加する傾向にあり、今回のモデルサイズでは遠距離での安定点を評価できませんでした。より広範囲の分布を調べるには、さらに大きなスーパーセルでの計算が必要です。
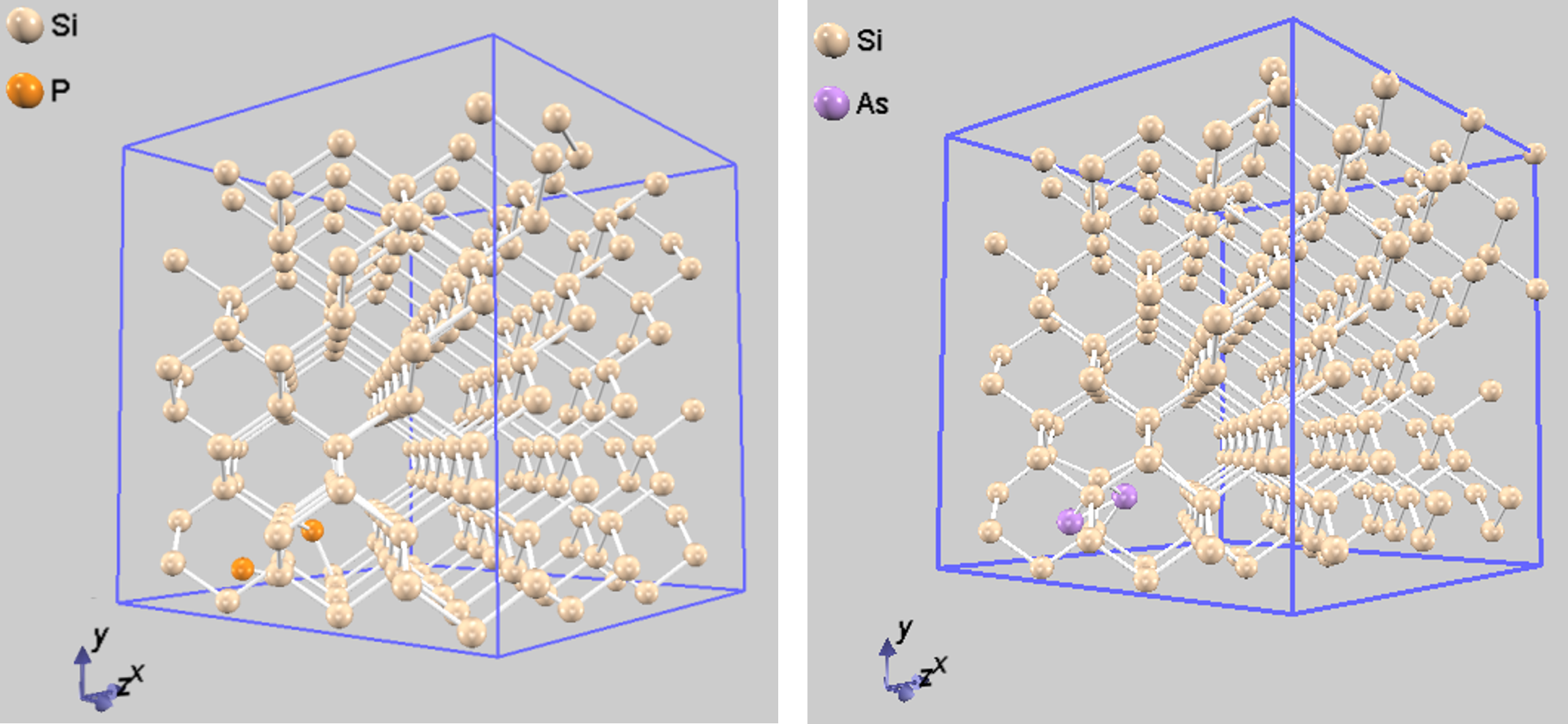
図6. (左) Pドーパントの安定化構造の例。(右) Asドーパントの安定化構造の例。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Si結晶中の代表なドーパント(B, P, As)の安定な分布を原子レベルで明らかにしました。計算結果は、ドーパント原子が単に拡散するだけでなく、元素種に依存した特有の相互作用を持ち、特定の原子間距離で安定化することを示しています。特にBやPでは、近距離でクラスタを形成する場合と、遠距離で孤立する場合の両方が安定となり得ることが分かりました。 このように、実験的測定が困難な原子レベルの構造とエネルギー安定性を定量的に評価できる第一原理計算は、半導体のドーピングプロセスの最適化や、より高性能なデバイスを設計するための強力なツールとなります。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- J. Zhu, T. Diaz de la Rubia, L. H. Yang, C. Mailhiot, and G. H. Gilmer, "Ab initio pseudopotential calculations of B diffusion and pairing in Si", Phys. Rev. B 54, 4741 (1996).
- X. Y. Liu, W. Windl, and M. P. Masquelier, "Ab initio modeling of boron clustering in silicon", Appl. Phys. Lett. 77, 2018 (2000).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学