DFTによる金属中の溶質・空孔結合エネルギーの第一原理計算: Al-Zn合金に対する考察#

PHASE logo

アルミニウム合金をはじめとする多くの金属材料において、溶質原子と空孔（原子のない空っぽの格子点）の相互作用は、材料の特性を決定する上で極めて重要です。特に、溶質・空孔結合エネルギー（Solute-Vacancy Binding Energy）は、「原子の拡散現象」や、合金の強度を左右する「時効・析出といった機械的特性」を理解し、制御するための基本的な物理量です。例えば、Al-Cu合金にSn（スズ）などを微量添加すると時効が抑制される現象は、Sn原子が空孔と強く結合し、Cu原子の拡散を妨げるために起こります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、アルミニウム(Al)中の亜鉛(Zn)不純物と空孔の結合エネルギーを高精度に算出するDFT手法と、その結果が持つ物理的な意義について考察します。

Keywords: 第一原理計算 (DFT), 溶質・空孔結合エネルギー, 空孔形成エネルギー, Al-Zn合金, スーパーセル法, k点収束性

計算モデルと計算条件#

DFT計算に用いたモデルは、Alのバルク結晶（最適化した格子定数 4.042 Å）から作成した2x2x2スーパーセル（32原子）をベースにしました。この完全結晶のセル（Al₃₂）に対し、Al原子1つをZn原子で置換したモデル（Al₃₁Zn₁）、Al原子1つを空孔(☐)にしたモデル（Al₃₁☐₁）、そしてZn原子と空孔が隣接したモデル（Al₃₀Zn₁☐₁）を構築しました。空孔の位置は、計算モデルにおいてダミー原子(X)を配置することで表現しています（図1）。

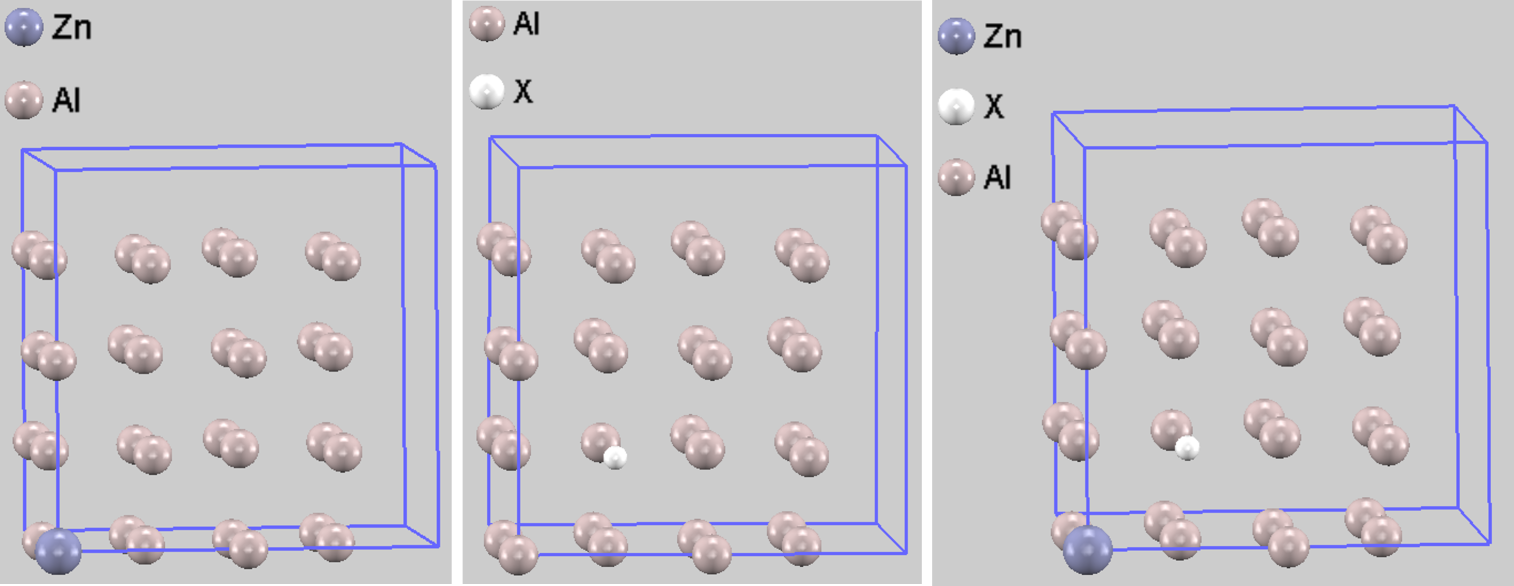
Al-Zn-Vacancy supercell models
図1.　計算に用いたスーパーセルモデル。(左) Al₃₁Zn（Zn不純物モデル）, (中) Al₃₁X（空孔モデル、Xはダミー原子）, (右) Al₃₀ZnX（Zn-空孔隣接モデル）。

本解析で用いた主な計算条件は表1に示されています。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	Zn:ウルトラソフト、 Al:ノルム保存
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Rydberg
k点サンプリング	4x4x4 から 16x16x16 で収束性テストを実施

計算結果と考察#

エネルギーの定義#

溶質・空孔結合エネルギー ( $E_{\text{binding}}$ ) は、溶質原子と空孔がそれぞれ孤立して存在する場合と、互いに隣接してペアを形成する場合のエネルギー差として定義されます。慣例に従い、正の値は引力（結合すると安定化）、負の値は斥力を意味します。計算式は以下の通りです：

$-E_{\text{binding}} = (E_{\text{solute+vacancy}} + E_{\text{perfect}}) - (E_{\text{solute}} + E_{\text{vacancy}})$

ここで、 $E_{\text{solute+vacancy}}$ は溶質と空孔が隣接したセルのエネルギー、 $E_{\text{perfect}}$ は欠陥のない完全結晶のエネルギー、 $E_{\text{solute}}$ は溶質原子が1つ置換したセルのエネルギー、 $E_{\text{vacancy}}$ は空孔が1つあるセルのエネルギーです。本解析のAl-Zn系（32原子セル）に当てはめると、以下のようになります：

$-E_{\text{bind}}(\text{Zn}-☐) = E(\text{Al}_{30}\text{Zn}_{1}☐_{1}) + E(\text{Al}_{32}) - E(\text{Al}_{31}\text{Zn}_{1}) - E(\text{Al}_{31}☐_{1})$

空孔形成エネルギー ( $E_{f}^{\text{vac}}$ ) は、完全結晶から原子を1つ取り除いて空孔を作るために必要なエネルギーです。スーパーセル計算では、以下の式で定義されます（ $N$ はスーパーセル内の原子数、本解析では $N$ =32）：

$E_{f}^{\text{vac}} = E(\text{Al}_{N-1}☐_{1}) - \frac{N-1}{N} E(\text{Al}_{N})$

これは、空孔を含むセルのエネルギー $E(\text{Al}_{N-1}☐_{1})$ から、同数の原子を含む完全結晶のエネルギー $E(\text{Al}_{N}) \times (N-1)/N$ を差し引いたものに相当します。

k点サンプリングの収束性#

スーパーセル法による欠陥計算では、k点メッシュの密度が結果に大きく影響することがあります。特に結合エネルギーのような微小なエネルギー差を評価する場合、十分な収束性の確認が必要です。表2に、k点メッシュの密度を変化させた場合の空孔形成エネルギー ( $E_{f}^{\text{vac}}$ ) とZn-空孔結合エネルギー ( $E_{\text{bind}}$ ) の計算結果を示します。

表2.　k点メッシュの密度と計算エネルギー値

K-Mesh	$E_{f}^{\text{vac}}$ (eV)	$E_{\text{bind}}$ (eV)
k4x4x4	0.687	0.113
k8x8x8	0.703	0.055
k12x12x12	0.641	0.036
k16x16x16	0.643	0.027

この結果から、空孔形成エネルギーは k12x12x12 程度で比較的早く収束する傾向が見られるのに対し、溶質・空孔結合エネルギーは k16x16x16 まで変化し続けており、高精度の計算には 2x2x2スーパーセルにおいても 16x16x16（FCCセル換算で 32x32x32）という非常に密なk点メッシュが必要であることが分かります。

文献値・実験値との比較#

k16x16x16で得られた本計算値を、報告されている実験値や他の計算値（文献値）と比較します。

空孔形成エネルギー:
本計算で得られたAlの空孔形成エネルギー 0.64 eV (表2のk16x16x16の値を丸めたもの) は、実験値（0.66 ± 0.03 eV、 0.62 ± 0.02 eV）と極めて良好な一致を示しています（表3）。

表3.　Alの空孔形成エネルギーの比較 (単位: eV)

項目	エネルギー (eV)
本計算値 (GGA/PBE)	0.64
実験値 [1]	0.66 ± 0.03
実験値 [2]	0.62 ± 0.02
文献値 (LDA) [3]	0.56

溶質・空孔結合エネルギー:
Al中のZn-空孔結合エネルギーについて、本計算値は 0.027 eV となりました。これも実験値 (0.02 eV) および他のGGA計算による文献値 (0.03 eV) と非常に良い一致を示しています（表4）。

表4.　Al中 Zn-空孔結合エネルギーの比較 (単位: eV)

項目	エネルギー (eV)
本計算値 (GGA/PBE, k16x16x16)	0.027
実験値 [2]	0.02
文献値 (GGA) [4]	0.03

結果の考察#

本計算および文献値から、Al中のZn-空孔結合エネルギーは約 0.03 eV と評価されました。この値が持つ物理的な意味について考察します。

1. 結合の性質と強さ:

引力: エネルギーが正の値（+0.03 eV）であるため、Zn原子と空孔の間にはエネルギー的に引力が働いていることを示します。
非常に弱い結合: しかし、0.03 eVという絶対値は熱エネルギーと比較しても非常に小さい値です。他の溶質元素、例えばAl合金の時効制御に用いられるSn（スズ）の結合エネルギー (0.25 eV) や In（インジウム） (0.20 eV) と比較すると、Znの結合力は1桁近く弱いことが分かります。文献 [4] でも、この値は「非常に弱い」結合と分類されています。

2. 拡散現象への影響:

この結合エネルギーが非常に弱いという事実は、Zn原子が空孔と出会っても、それを強く捕まえ続ける（トラップする）ことができないことを意味します。そのため、Zn原子の周りに空孔が局所的に集積することはなく、空孔濃度は純粋なAl中とほぼ同じと見なせます。Zn自体の拡散も、空孔をトラップすることによる影響は小さく、主に移動エネルギーと空孔形成エネルギーによって決まると考えられます。

3. 機械的特性（時効・析出）への影響:

アルミニウム合金の時効（析出硬化）は原子の拡散によって進行します。 SnやInのような微量添加元素が時効を「抑制」するメカニズム [4] は、これらの原子が空孔と強く結合（例：Sn 0.25 eV）し、他の主要な溶質原子（例：Cu）が拡散に使うための空孔を「枯渇」させるためです。 Znの結合エネルギー (0.03 eV) は、これらの強力なトラップ元素に比べて1桁近く弱いため、Znを微量添加しても、空孔トラップによる時効制御（抑制）効果は期待できません。 Zn自身はAl-Zn系合金で析出硬化に寄与する主要元素ですが、そのメカニズムは空孔トラップとは異なる（例：Guinier-Preston ゾーン形成など）ことが示唆されます [5]。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Al中のZn溶質と空孔の結合エネルギーの精密な評価を行いました。 2x2x2スーパーセルモデルにおいて、k点メッシュを 16x16x16 まで高密度に取ることで、結合エネルギーが 0.027 eV へと収束することを確認し、高精度な計算には十分なk点サンプリングが不可欠であることを示しました。得られた空孔形成エネルギー (0.64 eV) および溶質・空孔結合エネルギー (0.027 eV) は、実験値や他の計算文献値と非常に良好な一致を示しました。さらに、この 0.03 eV という結合エネルギーは「非常に弱い引力」を意味し、ZnがAl中で空孔を強くトラップする効果は持たず、SnやInのような時効制御（抑制）元素としては機能しないことが、第一原理計算のエネルギー評価から明らかになりました。このように、第一原理計算は、合金の巨視的な特性（拡散や時効）を支配する原子レベルの相互作用を定量的に解明する上で強力なツールとなります。

参考文献#

P. Tzanetakis, J. Hillairet, and G. Revel, "The formation energy of vacancies in aluminium and magnesium", physica status solidi (b) 75, 433 (1976).
C. L. Snead, Jr., T. M. Hall, and A. N. Goland, "Vacancy-impurity binding energy in aluminum—1.7 at.% zinc using positron-annihilation lifetimes", Phys. Rev. Lett. 29, 62 (1972).
M. J. Gillan, "Calculation of the vacancy formation energy in aluminium", J. Phys.: Condens. Matter 1, 689 (1989).
C. Wolverton, "Solute–vacancy binding in aluminum", Acta Materialia 55, 5867 (2007).
K. Osamura, Y. Hiraoka, and Y. Murakami, "The resistivity maximum during Guinier-Preston zone formation in Al-Zn alloys", Philosophical Magazine 28, 809 (1973).