コンテンツにスキップ

n型・p型半導体の電子状態とドーピング効果の解析#

Advance/PHASE logo

半導体の電気的特性は、不純物を添加するドーピングによって劇的に変化します。この特性制御は、ダイオードやトランジスタなど、あらゆる半導体デバイスの基本原理です。第一原理計算ソフトウェアAdvance/PHASEを用いることで、ドーピングが半導体の電子状態にどのような影響を与えるかを原子・電子レベルで詳細に解析することができます。ここでは、代表的な半導体であるシリコン（Si）にリン（P）をドープしたn型半導体と、アルミニウム（Al）をドープしたp型半導体を取り上げ、状態密度と電荷密度の計算からドーピング効果を明らかにします。

Keywords: 第一原理計算, 構造最適化, 局所状態密度, 部分電荷密度, n型半導体, p型半導体, ドーピング

計算手法#

本解析は、構造最適化と電子状態解析の2段階で行います。

  1. 構造最適化: まず、phaseソルバーを用いたSCF（自己無撞着場）計算により、ドーパント原子を含む系の原子配置を最適化し、最も安定な構造を求めます。

  2. 電子状態解析: 次に、最適化された構造と収束した電荷密度を基に、ekcalソルバーを用いたnon-SCF計算を実行します。これにより、電子状態をより密なk点メッシュで高精度に解析します。解析項目は下記です。

    • 状態密度 (DOS): 系の電子が取りうるエネルギー準位の分布を示します。ドーピングによってバンドギャップ内に新たな準位が形成される様子を捉えることができます。

    • 原子分割局所状態密度 (ALDOS): 全体の状態密度を原子ごとに分割して評価する手法です。 これにより、特定のエネルギー準位（例えばギャップ内準位）が、ホスト原子によるものか、あるいはドーパント原子に由来するものかを明確に区別できます。

    • 部分電荷密度: 特定のエネルギー範囲に存在する電子の空間的な分布を可視化する機能です。本解析では、フェルミ準位を基準として±0.1 eVのエネルギーウィンドウにおける部分電荷密度を計算しました。これにより、ギャップ内準位がどの原子を中心に、どのように空間的に広がっているかを直感的に理解することができます。

計算モデルと計算条件#

計算モデルとして、シリコンの2×2×2スーパーセル（計64原子）をベースとして用いました。このスーパーセルにあるSi原子1つを、n型半導体の場合はリン（P）原子に、p型半導体の場合はアルミニウム（Al）原子にそれぞれ置換しました。これにより、組成がSi63PおよびSi63Alのドープされたシリコンモデルを構築しました。構造最適化済みのモデルは図1に示します。

表1. 主な計算条件

項目 設定値
組成 n型: Si 63個, P 1個 / p型: Si 63個, Al 1個
交換相関汎関数 GGA-PBE
k点メッシュ SCF (構造最適化): 3×3×3
non-SCF (状態密度解析): 6×6×6
状態密度計算法 四面体法

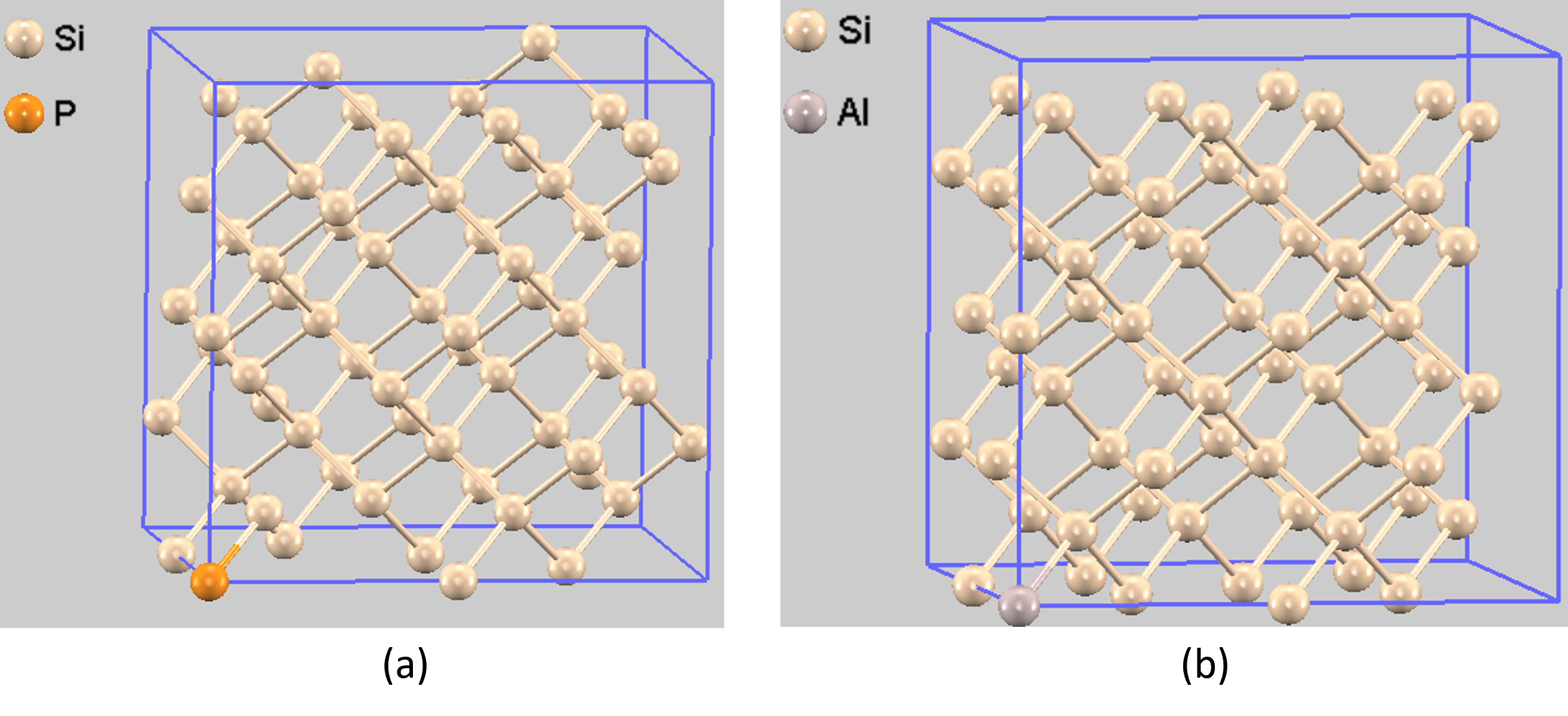
計算モデル(n型とp型)

図1. 計算モデル: (a) n型半導体モデルSi63P (b) p型モデルSi63Al

計算結果と考察#

1. n型半導体 (Si:P) の電子状態#

リン（P）をドープしたn型Siについて、全状態密度（Total DOS）、P原子の局所状態密度（ALDOS）、およびギャップ準位の部分電荷密度を評価しました。

全状態密度（図2）を見ると、本来電子が存在しないはずのバンドギャップ内に、伝導帯のすぐ下に隣接して新たな準位が発生していることが確認できます。これは、5価のP原子が持つ余剰電子によって形成されたドナー準位です。

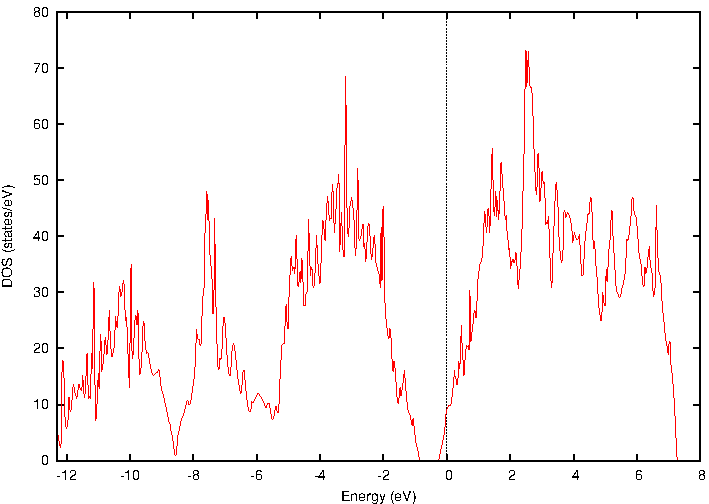
n型Siの全状態密度

図2.　n型Si(Si:P)の全状態密度。フェルミ準位が0 eVに設定されています。

P原子の局所状態密度（図3）は、隣接Si原子のLDOSや全状態密度とは大きく異なる形状を示します。特に、ギャップ内に現れたドナー準位がP原子のLDOSで顕著であり、この準位が主にP原子に起因するものであることがわかります。GGAを用いた計算ではバンドギャップが実験値より小さく見積もられる傾向がありますが、ドーパント準位の定性的な振る舞いを議論する上では問題となりません。

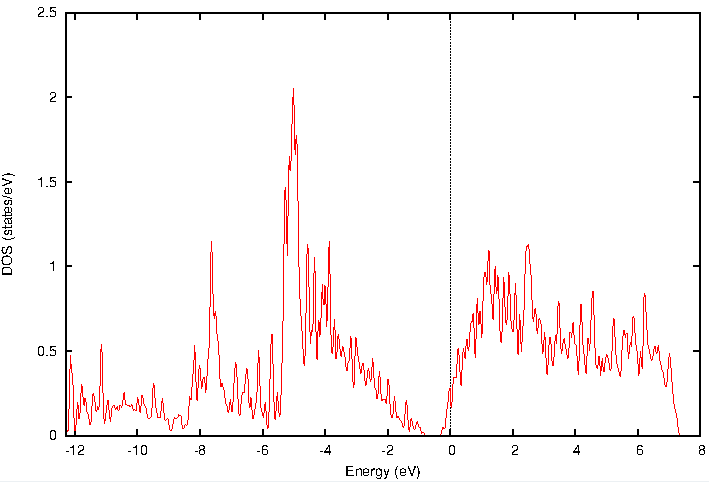
P原子の局所状態密度

図3.　P原子の局所状態密度。フェルミ準位が0 eVに設定されています。

ドナー準位に対応するエネルギー範囲の部分電荷密度を可視化しました（図4）。ここでは、電荷密度分布を等値面と断面図の両方で表現しています。どちらの図からも、電子雲がドナー原子であるPを中心に空間的に局在している様子が確認でき、ドナー準位がP原子に束縛された電子状態であることが視覚的にも裏付けられます。

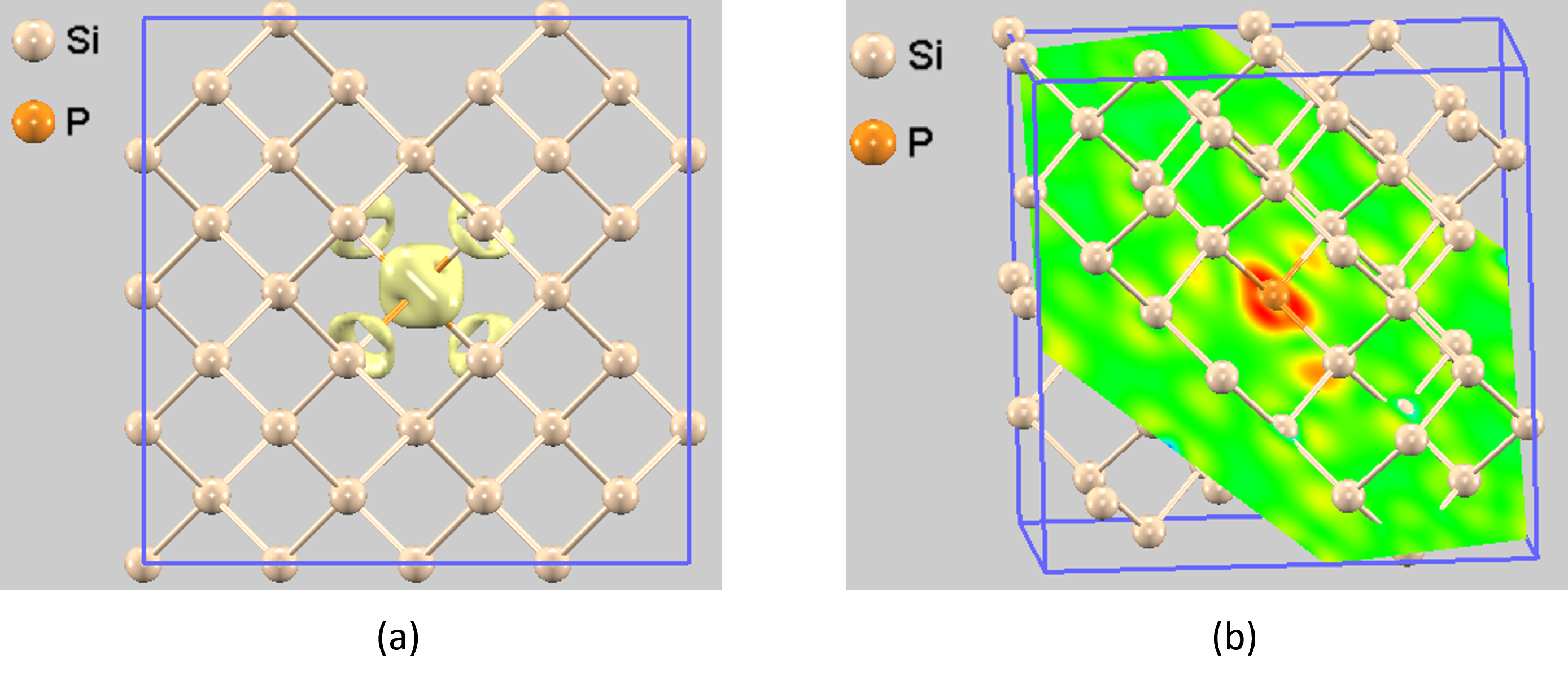
n型Siのギャップ準位の部分電荷密度

図4.　n型Siのドナー準位に対応する部分電荷密度: (a) 等値面 (b) 断面図。全体の並進移動でドナー原子Pをスーパーセルの中心位置に表現しています。

2. p型半導体 (Si:Al) の電子状態#

次に、アルミニウム（Al）をドープしたp型Siの電子状態を同様に解析しました。

全状態密度（図5）において、今度は価電子帯の上端に隣接してギャップ内準位が発生していることがわかります。これは、3価のAl原子が持つ電子の不足（正孔）によって形成されたアクセプター準位です。

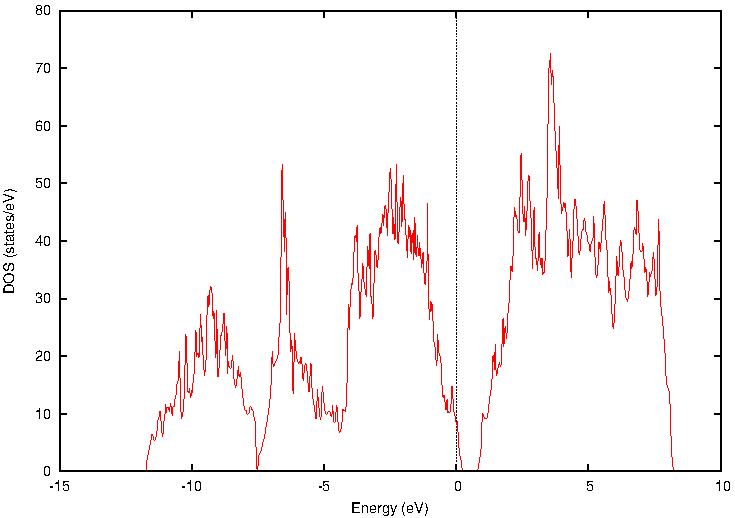
p型Siの全状態密度

図5.　p型Si(Si:Al)の全状態密度。フェルミ準位が0 eVに設定されています。

n型の場合と同様に、Al原子の局所状態密度（図6）は隣接Si原子のものとは大きく異なり、ギャップ内準位が主にAl原子に由来することを示唆しています。

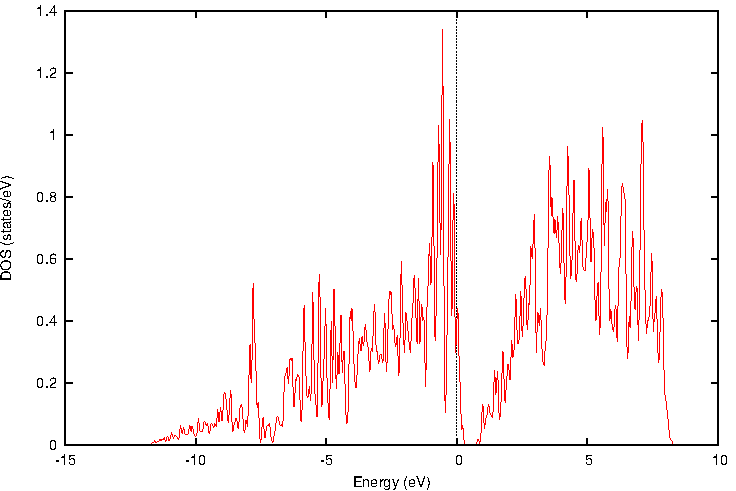
Al原子の局所状態密度

図6.　Al原子の局所状態密度。フェルミ準位が0 eVに設定されています。

ギャップ準位の部分電荷密度を解析しました（図7）。等値面と断面図で示すことで、電子が欠損した状態（正孔）がアクセプター原子であるAlを中心に広がっていることが視覚的に理解できます。

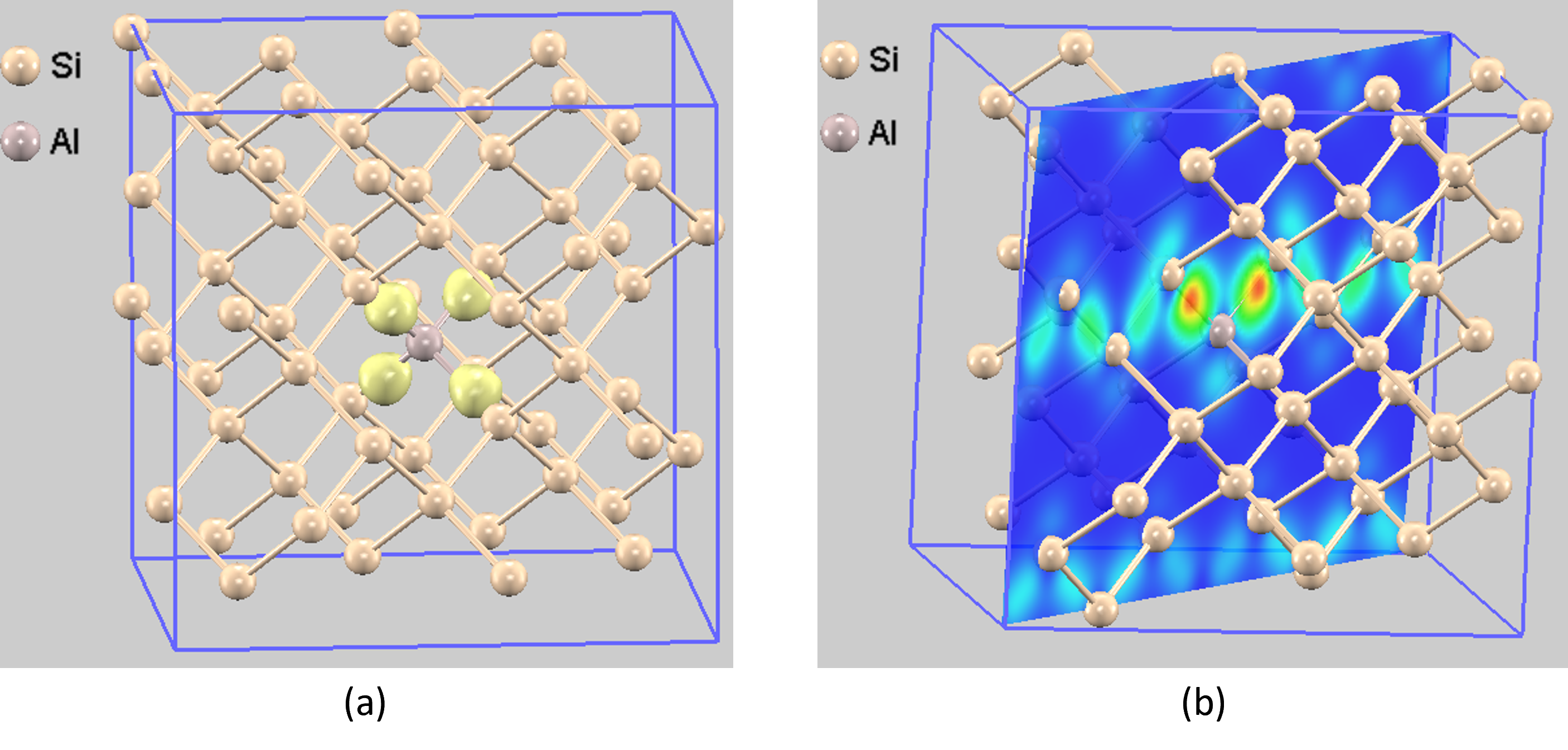
p型Siのギャップ準位の部分電荷密度

図7.　p型Siのアクセプター準位に対応する部分電荷密度: (a) 等値面 (b) 断面図。全体の並進移動でアクセプター原子Alをスーパーセルの中心位置に表現しています。

今回得られた、不純物添加によるバンドギャップ中の準位形成や、ドーパント原子周辺への電荷・正孔の局在といった計算結果は、半導体物理学の標準的な教科書で解説されている、浅い不純物の水素様モデルと定性的に良く一致するものです [1]。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、n型およびp型にドープされたシリコンの電子状態をシミュレーションしました。構造最適化を行った後の電子状態計算により、ドーピングによってバンドギャップ内に形成されるドナー準位（n型）およびアクセプター準位（p型）を明確に捉えることができました。さらに、原子分割局所状態密度と部分電荷密度の解析を組み合わせることで、これらのギャップ内準位がドーパント原子に強く局在した電子状態であることを明らかにしました。このように、第一原理計算はドーピングという半導体工学における根幹技術を、原子・電子レベルのミクロな視点から解明し、物性発現のメカニズムを深く理解するための極めて有効なツールです。

参考文献#

  1. P. Y. Yu and M. Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Springer (1996).

関連ページ#