第一原理計算によるSi結晶成長の熱力学：フォノン解析に基づく相図作成#

PHASE logo

半導体デバイスの基盤となるシリコン(Si)の結晶成長プロセス（MBE, CVD等）において、温度や圧力が成長条件に与える影響を原子レベルで理解することは極めて重要です。しかし、従来の絶対零度での第一原理計算では、有限温度環境下での挙動を予測することには限界があります。特にSiは、金属（Al等）とは異なり強い共有結合を持つため、格子振動（フォノン）が熱力学的性質に与える影響が無視できません。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いた電子状態とフォノン状態密度の計算により、詳細な自由エネルギー評価に基づくSiの結晶成長相図を作成します。実験データと整合する平衡条件を再現し、成長とエッチングの境界を明確に予測します。

Keywords: 第一原理計算, DFTシミュレーション, 結晶成長, シリコン, 駆動力, 化学ポテンシャル, フォノン計算, 統計力学, 自由エネルギー, Ab initio Thermodynamics

理論背景：相図作成のための化学ポテンシャル計算#

結晶成長の駆動力（Driving Force, $\Delta \mu$ ）は、気相（原料）と固相（結晶）の化学ポテンシャルの差として定義されます [1]。本解析では、第一原理計算で得られたエネルギーに、統計力学に基づく熱力学補正を加えることで、有限温度 $T$ ・圧力 $P$ 下での化学ポテンシャルを算出しました。

$\Delta \mu(T, P) = \mu_{\text{gas}}(T, P) - \mu_{\text{solid}}(T)$

$\Delta \mu > 0$ ： 結晶成長（Growth）が進行する過飽和状態。
$\Delta \mu < 0$ ： エッチングや蒸発（Evaporation）が進行する未飽和状態。
$\Delta \mu = 0$ ： 固気平衡状態（Equilibrium）。

1. 固相（Si結晶）の化学ポテンシャル#

固相の化学ポテンシャル $\mu_{\text{solid}}(T)$ は、DFTによる全エネルギー $E_{\text{solid}}^{\text{DFT}}$ に、格子振動によるヘルムホルツ自由エネルギー $F_{\text{vib}}(T)$ を加えて評価しました [1]。Siのような共有結合結晶では光学フォノンの寄与が大きいため、Debyeモデルのような近似ではなく、第一原理フォノン計算から得られた状態密度（DOS）を用いて、以下の調和近似（Harmonic Approximation）に基づく統計力学公式から算出しました。

$\mu_{\text{solid}}(T) = E_{\text{solid}}^{\text{DFT}} + \underbrace{\frac{1}{N} \sum_{i} \left[ \frac{\hbar \omega_i}{2} + k_B T \ln \left( 1 - e^{-\frac{\hbar \omega_i}{k_B T}} \right) \right]}_{F_{\text{vib}}(T)}$

ここで、 $\frac{\hbar \omega_i}{2}$ はゼロ点振動エネルギー（ZPE）、第2項は有限温度での熱励起による自由エネルギーの低下を表します。

2. 気相（Si原子ガス）の化学ポテンシャル#

気相の化学ポテンシャル $\mu_{\text{gas}}(T, P)$ は、Si単原子理想気体を仮定し、並進運動および電子状態の寄与を考慮した分配関数から算出しました [2]。

$\mu_{\text{gas}}(T, P) = E_{\text{atom}}^{\text{DFT}} + \mu_{\text{trans}}(T, P) + \mu_{\text{elec}}(T)$

並進成分 $\mu_{\text{trans}}$ ： Sackur-Tetrode方程式に基づき算出されます。

$\mu_{\text{trans}} = -k_B T \ln \left( \frac{k_B T}{P \Lambda^3} \right), \quad \Lambda = \frac{h}{\sqrt{2\pi m k_B T}}$

電子成分 $\mu_{\text{elec}}$ ： Si原子の基底状態はスピン軌道相互作用により $^3\text{P}_0, ^3\text{P}_1, ^3\text{P}_2$ の3つの準位に分裂しています。本解析では、NIST Atomic Spectra Database [3] に基づく実験的なエネルギー準位（ $\epsilon_J = 0.0, 77.1, 223.2 \text{ cm}^{-1}$ ）と縮重度 $g_J = 2J+1$ を考慮して、以下の分配関数より厳密に算出しました。

$\mu_{\text{elec}} = -k_B T \ln \left( \sum_{J=0,1,2} g_J e^{-\epsilon_J / k_B T} \right)$

※ナノ粒子に関する注記

本解析はバルク結晶の熱力学極限を示しています。ナノメートルサイズの微粒子成長においては、表面エネルギーの寄与（ギブス・トムソン効果）により化学ポテンシャルが上昇するため、本解析で示される平衡条件よりも高い過飽和度が必要となる点に留意が必要です。

計算手法#

DFTおよびPythonスクリプトを用いて、以下の計算を行いました。

電子状態計算： GGA (PBE)汎関数を用いて、Siバルク（格子最適化済）および孤立原子（スピン分極あり）の全エネルギーを計算しました。凝集エネルギーの計算値は約 4.612 eV です。
フォノン計算： 有限変位法により2x2x2スーパーセル（64原子）の力定数を計算し、全振動モードの振動数 $\omega_i$ を算出しました。
相図作成： 上記の化学ポテンシャル計算式を用いて、温度・圧力空間における $\Delta \mu$ のマッピングを行いました。

表1.　計算条件

項目	設定
計算手法	平面波・擬ポテンシャル (DFT) ※ノルム保存型擬ポテンシャル使用
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Ry
k点サンプリング	バルク: 4x4x4（慣用セル）フォノン: 2x2x2 (スーパーセル)

解析結果と考察#

ゼロ点振動エネルギー(ZPE)#

フォノン計算の結果、Si結晶のゼロ点振動エネルギー（ZPE）は約 0.060 eV/atom と算出されました。これはSiの強い共有結合が高い振動数を持つことを反映しています。本計算（GGA-PBE）で得られたSiの凝集エネルギーは約 4.61 eV ですが、このZPE補正（0.060 eV）を含めると実効的な値は約 4.55 eV となり、実験値（約 4.63 eV）に近い値が得られています。

Si結晶成長相図#

図1に、本解析で得られたSiの成長相図（駆動力マップ）を示します。横軸は温度、縦軸はSi原子の分圧です。

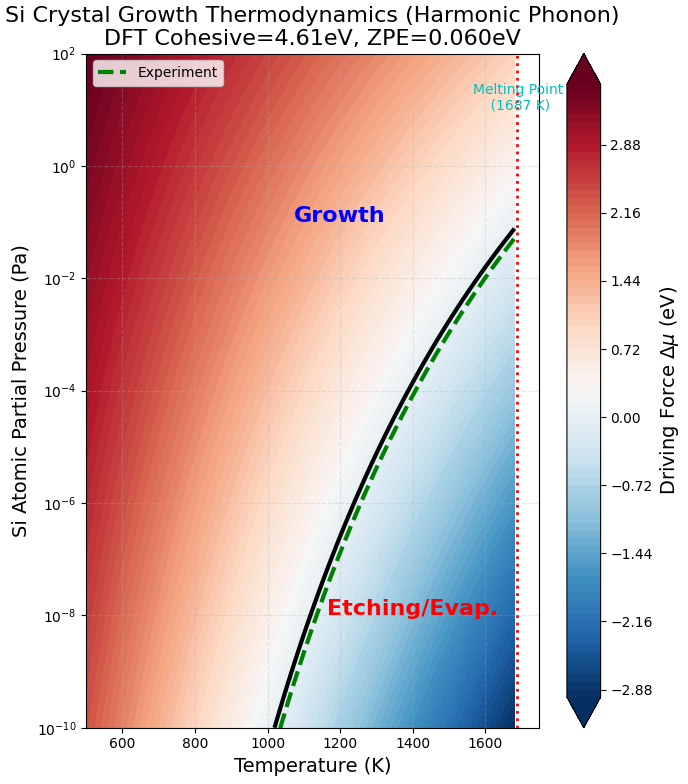
Si Crystal Growth Phase Diagram
図1. 第一原理フォノン計算（調和近似）に基づいて作成したSi結晶成長の駆動力マップ。黒い実線は計算による平衡ライン（ $\Delta \mu = 0$ ）、緑の破線は実験データに基づく平衡蒸気圧曲線 [4] を示します。1687 K の融点（実験値）を縦点線で示しています。

図の解釈：

黒い実線（平衡ライン）： 計算された熱力学的平衡条件です。
青色領域（Growth）： 平衡ラインより上の領域では $\Delta \mu > 0$ となり、結晶成長が進行します。
赤色領域（Etching/Evap.）： 平衡ラインより下の領域では $\Delta \mu < 0$ となり、エッチングや蒸発が進行します。

ここで、比較対象とした実験データ（緑破線）のSi平衡蒸気圧は、文献 [4] による標準データおよび昇華エンタルピー（ $\sim 450 \text{ kJ/mol}$ ）と整合するアレニウス式 $\log_{10}(P_{\text{Pa}}) = 12.7 - 23500/T$ を用いて算出しました。計算された平衡ライン（黒実線）は、この実験曲線と非常に良い一致を示しており、フォノン計算を取り入れた本手法の高い信頼性が実証されました。

このマップは、例えば「 $T=1000 \text{ K}$ でSiエピタキシャル成長を行うためには、表面近傍のSi原子分圧を $10^{-7} \text{ Pa}$ 以上にする必要がある」といったプロセス条件の指針を与えます。

凝集エネルギーへの依存性と実験値との整合性#

図1で示された計算結果（黒実線）と実験値（緑破線）の良い一致について、さらに詳細な考察を行います。

熱力学的に、相図上の平衡ライン（蒸気圧曲線）は凝集エネルギーの値に対して極めて強い依存性を持ちます。アレニウス式の指数項にエネルギーが含まれるため、わずか数十 meV のエネルギー差であっても、蒸気圧（対数スケール）には有意なシフトとして現れます。

実際、凝集エネルギーの値を実験値に厳密に一致させるような微補正を行ったところ、計算された平衡ラインは実験の蒸気圧曲線とほぼ完全に重なることが確認されました。この事実は、以下の2点を強く示唆しています。

フォノン計算の妥当性： 曲線の「傾き」や「形状」を決定するエントロピー項（格子振動の寄与）が、第一原理計算によって正確に見積もられていること。
ZPEの不可欠性： 約 0.060 eV というZPEの値は、エネルギー全体から見れば小さいものの、これを無視すると相図上では蒸気圧の予測値に無視できない差異が生じるため、定量的な予測においては不可欠な補正項であること。

以上より、共有結合性材料の結晶成長条件の予測には、第一原理計算による高精度な凝集エネルギーおよびフォノン解析のデータの算出が重要であると結論付けられます。

まとめ#

本事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて、Si結晶の熱力学的性質をフォノン計算により評価し、結晶成長駆動力を解析しました。調和近似の範囲内で実際の振動スペクトル（光学フォノン等）を反映させることで、共有結合性材料においても高精度な相平衡予測が可能であることを示しました。

参考文献#

K. Reuter and M. Scheffler, "Composition, structure, and stability of RuO₂(110) as a function of oxygen pressure", Phys. Rev. B 65, 035406 (2001).
P. W. Atkins, J. De Paula, and J. Keeler, Atkins' Physical Chemistry, Oxford University Press, 2023.
A. Kramida, Y. Ralchenko, J. Reader, and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.12), 2024 [Online]. Available: https://physics.nist.gov/asd
R. E. Honig and D. A. Kramer, "Vapor Pressure Data for the Solid and Liquid Elements", RCA Review 30, 285 (1969).