第一原理計算を用いたAl結晶成長駆動力の熱力学的解析：薄膜成長条件の予測と相平衡#

PHASE logo

薄膜形成プロセスにおいて、温度や圧力といった実験パラメータが成長駆動力に与える影響を理解することは、高品質な結晶を得るための鍵となります。しかし、従来の第一原理計算は絶対零度・真空中という理想環境を前提としているため、そのままでは現実の実験条件（有限温度・ガス雰囲気下）との直接的な比較が困難です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いた電子状態計算に、統計力学的な補正（Ab initio Thermodynamics）を組み合わせることで、有限温度・圧力下におけるアルミニウム(Al)の結晶成長駆動力を定量的に評価します。実験データと整合する平衡条件を再現し、結晶成長が促進される条件（過飽和）と、蒸発・エッチングが進行する条件を明確に区別可能な「成長相図」の作成を行います。

Keywords: 第一原理計算, DFTシミュレーション, 結晶成長, 薄膜成長, 駆動力, 化学ポテンシャル, 過飽和度, Ab initio Thermodynamics, Debyeモデル, NIST Shomate式, アルミニウム

理論背景：化学ポテンシャルと駆動力#

結晶成長の駆動力（Driving Force, $\Delta \mu$ ）は、原料供給源（気相など）と生成相（結晶）の化学ポテンシャルの差として定義されます。気相中の原子が結晶表面に取り込まれて成長する場合、気相のポテンシャルが固相よりも高い状態、すなわち以下の条件を満たす必要があります。

$\Delta \mu(T, P) = \mu_{\text{gas}}(T, P) - \mu_{\text{solid}}(T) > 0$

ここで、 $\mu_{\text{gas}}$ （気体の化学ポテンシャル）は温度 $T$ と圧力 $P$ に依存して大きく変化するのに対し、 $\mu_{\text{solid}}$ （固体の化学ポテンシャル）は主に温度のみに依存します。

$\Delta \mu > 0$ ： 成長（Growth）が進行します（過飽和状態）。
$\Delta \mu < 0$ ： 蒸発・エッチング（Evaporation/Etching）が起こります。
$\Delta \mu = 0$ ：熱力学的な平衡状態（Equilibrium）です。

※薄膜成長およびナノ粒子形成に関する注記

本解析は、表面エネルギーの影響が無視できる十分なサイズを持ったバルク結晶の熱力学量に基づいています。実際の薄膜成長の初期段階（核生成）やナノ粒子の形成過程においては、表面エネルギーや基板との界面エネルギーの影響が支配的になります。そのため、核生成を伴う実際の成長プロセスには、本解析で示される平衡条件よりも高い過飽和度（より高い圧力または低い温度）が必要となる点にご留意ください。

第一原理熱力学によるモデル化#

本解析では、気相および固相の化学ポテンシャルを、第一原理計算で得られた全エネルギーと熱力学的な補正項を用いて以下のようにモデル化しました [1]。

1. 気相（原料ガス）の化学ポテンシャル 理想気体近似に基づき、孤立原子のDFTエネルギー $E_{\text{atom}}^{\text{DFT}}$ に、並進・回転・振動運動による熱補正項を加えます。本解析では、熱補正項（エンタルピー変化 $\Delta H_{\text{gas}}$ およびエントロピー $S_{\text{gas}}$ ）の算出に、NIST Shomate式 [2] を採用しました。これにより、NIST-JANAF熱化学表などの実験データを滑らかに補間し、任意の温度における高精度な熱力学量を取り込んでいます。

$\mu_{\text{gas}}(T, P) = E_{\text{atom}}^{\text{DFT}} + \underbrace{\Delta H_{\text{gas}}(T, P^0) - T S_{\text{gas}}(T, P^0)}_{\text{NIST Shomate式による補正}} + k_B T \ln \left( \frac{P}{P^0} \right)$

2. 固相（Al結晶）の化学ポテンシャル バルク結晶のDFTエネルギー $E_{\text{solid}}^{\text{DFT}}$ に、格子振動による自由エネルギー $F_{\text{vib}}(T)$ を加えます。

$\mu_{\text{solid}}(T) = E_{\text{solid}}^{\text{DFT}} + F_{\text{vib}}(T)$

Debyeモデルによる格子振動の評価と実用的アプローチ#

固体の振動自由エネルギー $F_{\text{vib}}(T)$ の算出には、一般的にフォノン状態密度（Phonon DOS）の積分が必要です。Advance/PHASEは「有限変位法」によるフォノン計算機能を搭載しておりますが、熱力学量の収束には比較的大きなスーパーセル（高い計算コスト）を要する場合があります。

本解析では、多数の条件検討や材料スクリーニングを見据えた「実用的なワークフロー」を提示するため、より簡便かつ計算負荷の低いDebyeモデルを採用しました。Alのような等方的なfcc金属において、Debyeモデルは実験値を良好に再現することが知られており、最小限の計算資源で信頼性の高い相図を作成するのに適した選択と言えます。

具体的な計算パラメータとして、本解析ではAlのDebye温度 $\Theta_D = 428 \text{ K}$ を用い、ゼロ点振動エネルギー（Zero Point Energy: ZPE）および有限温度での自由エネルギーを考慮しました。

計算方法#

DFT計算において、以下の2つの系について構造最適化および全エネルギー計算を行いました。

Al バルク結晶（fcc構造）: 固相の基準エネルギー $E_{\text{solid}}^{\text{DFT}}$ を算出するため、単位格子を用いて計算しました。
Al 孤立原子: 気相の基準エネルギー $E_{\text{atom}}^{\text{DFT}}$ を算出するため、十分な大きさのスーパーセル（真空領域）中にAl原子を1つ配置し、スピン分極を考慮して計算しました。

計算条件の概要を表1に示します。

表1.　計算条件

項目	設定
擬ポテンシャル	ノルム保存型
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	30 Ry
k点サンプリング	バルク: 12x12x12 孤立原子: 1x1x1 ( $\Gamma$ 点のみ)

解析結果と考察#

成長相図（駆動力マップ）の構築と解釈#

計算結果に基づき作成した「Al結晶の成長相図（駆動力マップ）」を図1に示します。この図は、プロセス条件（温度と圧力）と結晶成長の可否を即座に判断するための指針（ガイドライン）となります。

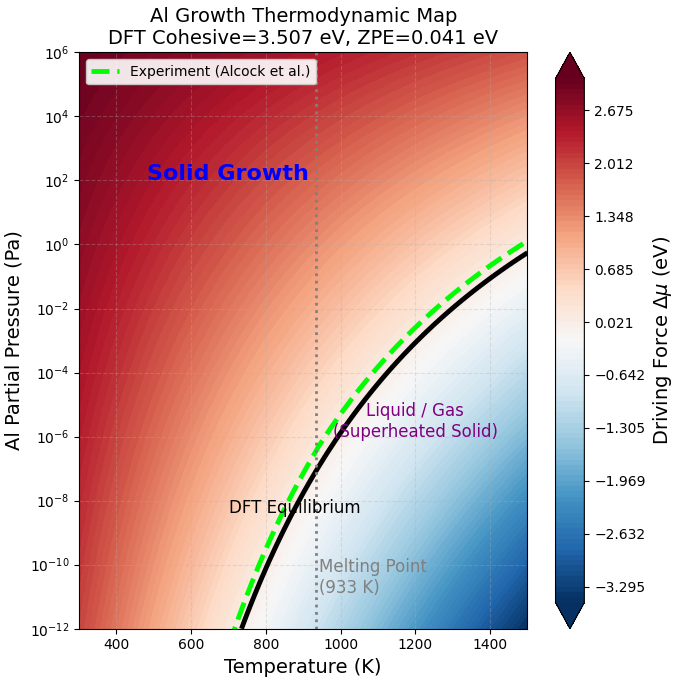
Al Crystal Growth Driving Force Map calculated by DFT + Debye Model
図1.　第一原理計算とDebyeモデルに基づいて作成したAl結晶成長の駆動力マップ。黒い実線は計算による平衡ライン（ $\Delta \mu = 0$ ）、緑の破線は実験データに基づく平衡蒸気圧曲線 [3]。Alの融点（933 K, 実験値）の位置を縦の点線で示しています。933 K以上は液相（Liquid）が安定であり、通常の結晶成長（Solid Growth）とは異なります。

図の解釈と注意点：

黒い実線（平衡ライン）： $\Delta \mu = 0$ となる条件です。ここでは成長速度と蒸発速度が釣り合っています。
赤い領域（Solid Growth）： 平衡ラインより上の領域（圧力が高い、または温度が低い）です。ここでは $\Delta \mu > 0$ となり、結晶成長が進行します。色が濃いほど駆動力が大きく、高い成長速度が期待できます。ただし、図の縦点線で示されている融点（933 K）以上の温度領域では液相が安定となるため、通常の結晶成長（Solid Growth）とは異なる挙動になります。

実験値との整合性とモデルの妥当性#

図1において、計算値（黒実線）と実験値（緑破線）は概ね良い一致を示しており、Debyeモデルを用いた熱力学補正が有効に機能していることが分かります。

より詳細に見ると、計算による平衡ラインは実験値よりもわずかに低圧側（あるいは高温側）にシフトしています。GGA-PBEで凝集エネルギーの計算値は 3.51 eVであり、実験値（3.39 eV）に対してわずかに過大評価となっています。実際、凝集エネルギー（ZPEを含む）を実験値相当の 3.39 eV に補正してプロットすると、平衡ラインは実験データとほぼ完全に一致することを確認しました。このことから、本解析で用いた熱力学モデル自体は高い妥当性を有しており、汎関数によるエネルギー誤差（約 0.1 eV）を考慮すれば、実験結果を定量的に再現可能であることが示されました。

プロセス設計への応用#

このマップを用いることで、MBE（分子線エピタキシー）や真空蒸着といったPVDプロセスにおいて、「温度 800 K でAl薄膜を成長させるために必要なAlビーム等価圧力」などを理論的に予測することができます。試行錯誤を減らし、最適な成長条件を効率的に探索するための有力なツールとなります。

まとめ#

本事例では、第一原理計算ソフトウェアAdvance/PHASEによるDFT計算にAb initio Thermodynamicsの手法を適用し、Al薄膜の結晶成長駆動力を解析しました。NIST Shomate式による気相の熱力学補正と、Debyeモデルによる固相の振動効果を考慮することで、現実的な温度・圧力環境下での相平衡を再現し、成長と蒸発の境界を明確に示す相図を作成しました。本手法は、実験データの乏しい新規材料の合成条件探索や、広範な温度・圧力条件下での材料の熱力学的安定性（相平衡）評価にも広く応用可能です。

参考文献#

K. Reuter and M. Scheffler, "Composition, structure, and stability of RuO₂(110) as a function of oxygen pressure", Phys. Rev. B 65, 035406 (2001).
NIST Chemistry WebBook, SRD 69, "Aluminum (Gas Phase) Thermochemistry Data". (Shomate Equation coefficients)
C. B. Alcock, V. P. Itkin, and M. K. Horrigan, "Vapour Pressure Equations for the Metallic Elements: 298–2500K", Canadian Metallurgical Quarterly 23, 309 (1984).