絶縁体BNナノチューブの電子状態解析#

PHASE logo

窒化ホウ素ナノチューブ（Boron Nitride Nanotube: BNNT）は、カーボンナノチューブ（CNT）と同様の構造を持ちながら、そのカイラリティ（巻き方）に依存せず、金属化することなく常にバンドギャップを持つ絶縁体（ワイドギャップ半導体）であるという特徴があります。また、優れた熱的・化学的安定性や機械的強度を有することから、絶縁性放熱材料や複合材料の強化フィラーとしての応用が期待されています。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、アームチェア型BNNT(5,5)の構造最適化および電子状態解析を行い、その力学的特性と絶縁体としてのバンド構造を評価します。

Keywords: 第一原理計算, DFTシミュレーション, BNナノチューブ, BNNT(5,5), 絶縁体, バンド構造, 構造最適化, ヤング率

計算モデルと計算条件#

DFT計算のモデルには、アームチェア型であるBNNT(5,5)を用いました。図1(a)に計算セル全体、(b)に正面図を示します。チューブ軸（c軸）方向に周期境界条件を適用し、チューブ間の相互作用を排除するため十分な真空領域 (約20 Å)を設けています。

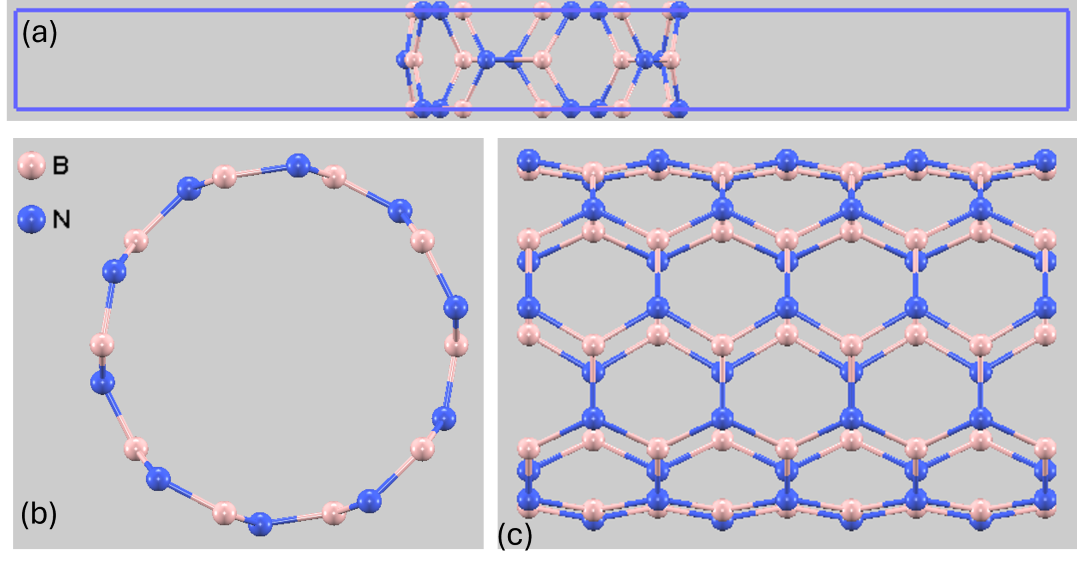
図1.　BNNT(5,5)の計算モデル: (a) 全体を示す計算セル、 (b) BNNTの正面図、 (c) 視認性を高めるため、チューブ軸方向に周期を4倍して表示した側面図

計算は密度汎関数理論（DFT）に基づき、平面波基底・擬ポテンシャル法を用いて実施しました。主な計算条件は表1の通りです。BNNTは絶縁体であるため [1]、SCF計算には非金属設定を用いて計算コストを削減しています。なお、事前の収束性検証において、カットオフエネルギーを30 Ryとした場合でもヤング率の変動は0.4%未満であり、本計算条件（35 Ry）で十分な精度が得られていることを確認しています。

表1.　主な計算条件

項目	設定
交換相関汎関数	GGA-PBE
擬ポテンシャル	ウルトラソフト擬ポテンシャル
カットオフエネルギー	35 Rydberg
k点サンプリング	1 x 1 x 6 (SCF計算) 1 x 1 x 36 (DOS計算)

計算結果と考察#

1. 格子定数の最適化と機械的特性#

BNNT(5,5)の安定構造を決定するため、チューブ軸方向の格子定数 $c$ を変化させて構造最適化を行いました。エネルギー曲線の解析（図2）から、最適な格子定数 $c_0$ は 2.5164 Å と求まりました。

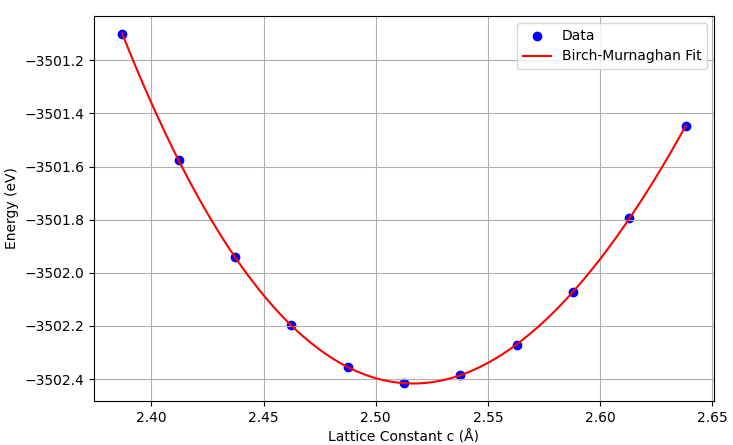
格子定数の最適化グラフ
図2.　格子定数 $c$ に対する全エネルギーの変化とBirch-Murnaghanフィッティング

さらに、このエネルギー変化をBirch-Murnaghanの状態方程式でフィッティングし、機械的強度を算出しました。ヤング率 $Y$ は、以下の式に基づき、ひずみ $\varepsilon$ に対する全エネルギー $E$ の2階微分から求められます。

$Y = \frac{1}{V_0} \left. \frac{\partial^2 E}{\partial \varepsilon^2} \right|_{\varepsilon=0}$

ここで、 $V_0$ は平衡時の体積 ( $V_0 = S \times c_0$ ) です。ナノチューブのような中空構造を持つ低次元系では、ヤング率の絶対値は断面積 $S$ （すなわちチューブ壁の有効厚さ）の定義に強く依存します。本解析では、先行研究 [2] との定量的な比較を整合させるため、慣例に従いグラファイトの層間距離（3.4 Å）を有効厚さと定義して断面積を算出しました。

その結果、算出されたヤング率 $Y$ は 777.1 GPa (約0.78 TPa) となりました。この値は、同様の定義を用いた先行研究による理論計算値（0.79 TPa）[2] と良い一致を示しており、本計算手法の妥当性が確認されました。

BNNTの機械的性質については、カーボンナノチューブ（CNT）と同様に極めて強固であることが知られていますが、文献 [3]のDFT計算により、BNNTがCNTよりもさらに高い破壊耐性を持つ可能性が指摘されています。その研究によると、引張応力下で発生する構造欠陥（転位双極子）の形成エネルギーは、CNTよりもBNNTの方が高く、より大きな歪みまで構造を維持できると予測されています。今回の計算で確認された高いヤング率は、このようなBNNTの優れた機械的安定性を裏付けるものです。

2. 電子状態：バンド構造と状態密度#

最適化された構造を用いて電子状態を計算しました。図3に状態密度（DOS）、図4にバンド構造を示します。

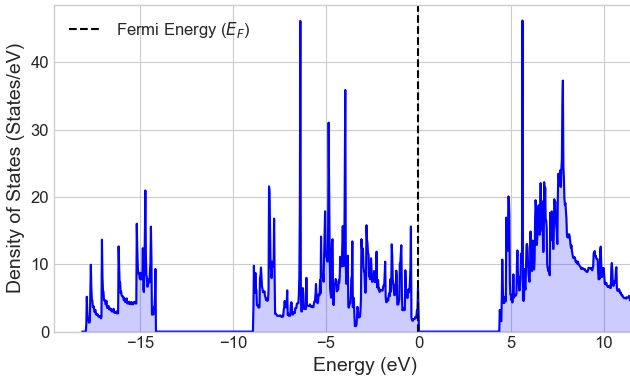
図3.　BNNT(5,5)の状態密度（DOS）

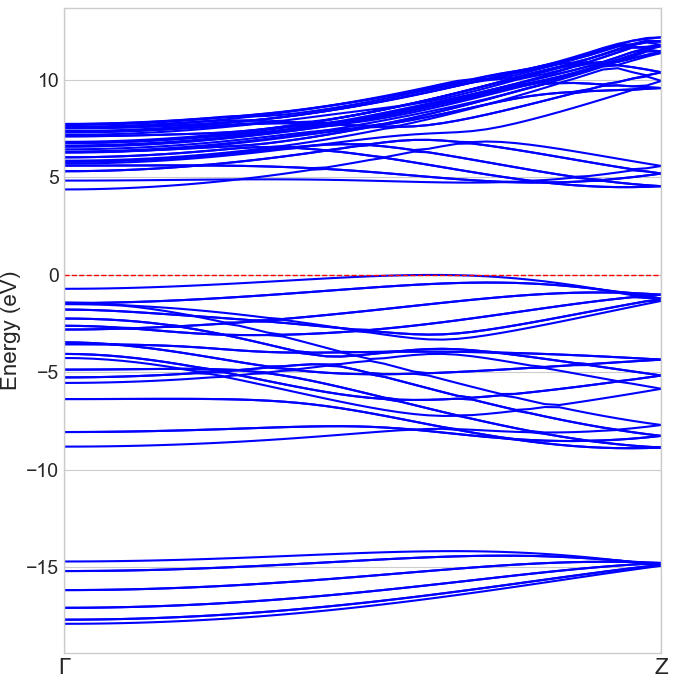
図4.　BNNT(5,5)のバンド構造

状態密度およびバンド構造から、フェルミエネルギー（0 eV）付近にバンドが存在せず、明確なエネルギーギャップが開いていることがわかります。計算されたバンドギャップは約4.36 eVでした。実験的にはBNNTのバンドギャップは約5.5 eVと報告されていますが [1]、一般に、GGA近似を用いたDFT計算では、バンドギャップが過小評価される傾向があります。実際、文献 [4]でのDFT計算でもBNNT(5,5)チューブのバンドギャップは4.5 eVと報告されており [4]、本計算結果はこれと良い一致を示しています。

なお、より実験値に近い定量的な評価が必要な場合には、ハイブリッド汎関数（HSE06等）を用いることで、バンドギャップの過小評価を補正することも可能です。本事例では計算コストと精度のバランスを考慮しGGA-PBEを採用しましたが、同形状のCNT(5,5)が金属性を示すのに対し、BNNTは広いギャップを有する絶縁体となる、という重要な特徴は正しく再現されています。

3. 電荷密度分布と結合の性質#

BNNTが絶縁体となる微視的な起源、およびその特異な電子物性を探るため、電荷密度分布を詳細に解析しました。

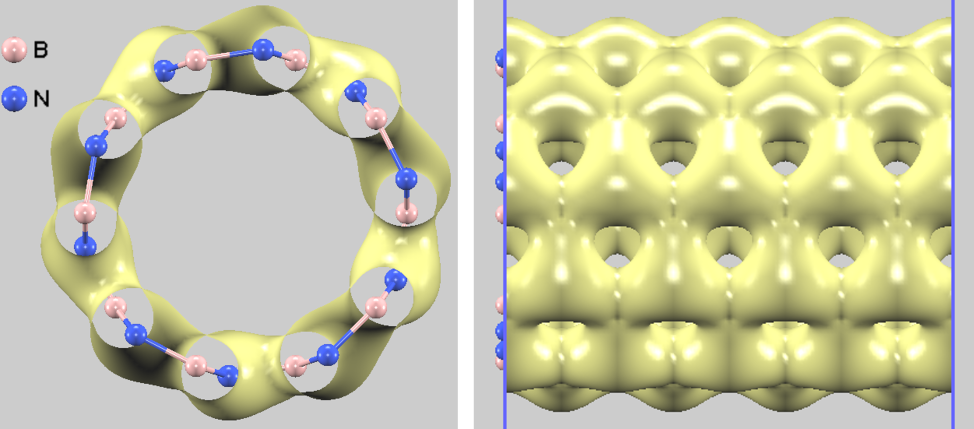
全電荷密度分布の等値面
図5.　全電荷密度の等値面。電子密度はチューブの骨格に沿って分布しており、B-N間の強固な結合ネットワークが形成されていることがわかります。

全電荷密度（図5）はB-N結合の共有結合性を示していますが、バンドギャップを挟んだ価電子帯頂上（VBM）と伝導帯底（CBM）の部分電荷密度（波動関数）を確認すると、BNNT特有の興味深い電子状態が明らかになります。

価電子帯頂上（VBM）：窒素原子への強い局在#

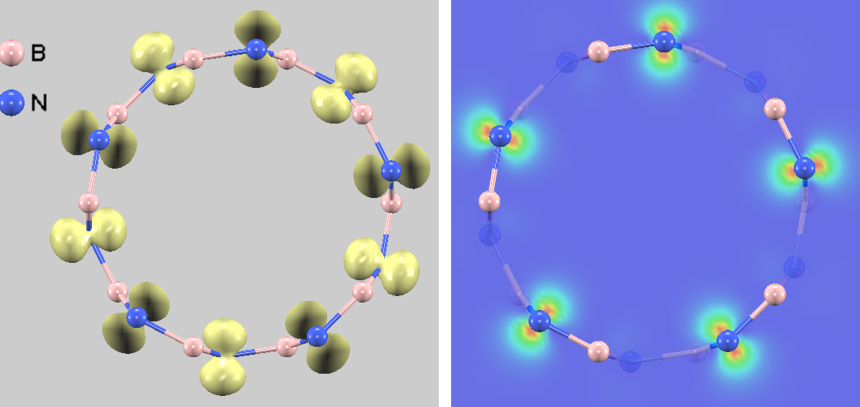
VBMの部分電荷密度分布
図6.　価電子帯頂上（VBM）の部分電荷密度分布。[左] 等値面表示、[右] チューブ断面のコンター図（線形スケール）。

図6に示すように、VBMの電子は電気陰性度の大きい窒素（N）原子（青色球）の周囲に強く局在しています。等値面および線形スケールのコンター図（断面図）の双方において、電子密度が高い領域（赤色～黄色）はN原子近傍のp軌道にはっきりと限定されており、真空領域への広がりはほとんど見られません。

伝導帯底（CBM）：ホウ素への局在と真空への染み出し#

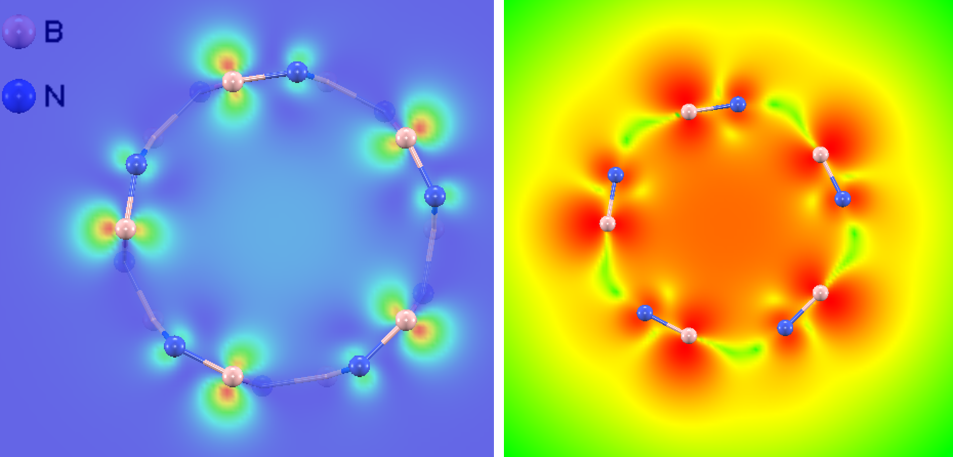
CBMの部分電荷密度コンター図
図7.　伝導帯底（CBM）の部分電荷密度コンター図。[左] 線形スケール表示、[右] 対数スケール表示。

一方、図7のCBMの電子分布は、表示スケールを変えることでその二面性が浮き彫りになります。

線形スケール（左図）： 電子密度の主成分はホウ素（B）原子（ピンク色球）の近傍にあり、カチオン的な性質を示しています。
対数スケール（右図）： 低密度領域を強調して表示すると、チューブ内部の空洞や外側の真空領域にも電子密度が広く染み出していることが鮮明に確認できます。

この「真空への染み出し」は、BNナノチューブの幾何学的な曲率によって形成される自由電子的な状態（Near Free Electron state: NFE）と呼ばれる特異なものです [5]。電子は原子核に強く束縛されず、チューブの内外に「浮いた」ような分布をとります。このCBM（ホウ素への局在と真空への染み出し）とVBM（窒素原子への強い局在）の空間的な分離が、BNNTの高い絶縁性の要因の一つとなっており、同時に、チューブ表面に束縛されないキャリア輸送や、特異なドーピング特性を持つ可能性を示唆しています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いてBNナノチューブ(5,5)の電子状態と機械的特性を評価しました。構造最適化により得られたヤング率は約0.78 TPaであり、BNNTが優れた機械的強度を持つという既存の研究結果と整合します。また、電子状態解析により、約4.36 eVのバンドギャップを持つ絶縁体であることが確認されました。この値は先行研究の理論計算値（4.5 eV）と良く一致しています。さらに、VBMとCBMの電荷密度分布の解析から、電子が窒素原子へ、ホールがホウ素原子へ局在化していることが視覚的に示され、このイオン性がBNNTの絶縁特性の起源であることが明らかになりました。

本解析の詳細や、研究への適用可能性に関するご相談はこちら

お問い合わせ

参考文献#

N. G. Chopra, R. J. Luyken, K. Cherrey, V. H. Crespi, M. L. Cohen, S. G. Louie, and A. Zettl, "Boron Nitride Nanotubes", Science 269, 966 (1995).
I. K. Petrushenko and K. B. Petrushenko, “Mechanical properties of carbon, silicon carbide, and boron nitride nanotubes: effect of ionization”, Monatshefte für Chemie-Chemical Monthly 146, 1603 (2015).
H. F. Bettinger, T. Dumitrică, G. E. Scuseria, and B. I. Yakobson, "Mechanically induced defects and strength of BN nanotubes", Phys. Rev. B 65, 041406 (2002).
C. Zhi, Y. Bando, C. Tang, and D. Golberg, "Engineering of electronic structure of boron-nitride nanotubes by covalent functionalization", Phys. Rev. B 74, 153413 (2006).
X. Blase, A. Rubio, S. G. Louie, and M. L. Cohen, "Stability and Band Gap Constancy of Boron Nitride Nanotubes", Europhys. Lett. 28, 335 (1994).