様々な物質の凝集エネルギーの第一原理計算#

材料の安定性や結合の強さを評価する上で、凝集エネルギー (Cohesive Energy)は最も基本的かつ重要な物理量の一つです。凝集エネルギーとは、互いに無限に離れたばらばらの原子が集まって結晶を形成する際に放出されるエネルギーのことであり、その値が大きいほど、より強く結合し安定な物質であることを示します。新材料の探索や既存材料の物性理解において、凝集エネルギーを正確に予測することは極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、周期表にわたる様々な元素の凝集エネルギーを計算し、その結果を実験値と比較します。この比較（パリティプロット）を通じて、Advance/PHASEが多様な物質の安定性をどの程度正確に予測できるかを検証します。

Keywords: 第一原理計算, 凝集エネルギー, 形成エネルギー, 密度汎関数理論, パリティプロット

理論背景と計算方法#

第一原理計算におけるエネルギーの原点#

第一原理計算で算出される「全エネルギー」の絶対値は、それ自体に直接的な物理的意味を持ちません。これは、エネルギーの基準点（ゼロ点）が、使用する擬ポテンシャルの種類や計算モデルに固有の形で設定されるためです。この基準点は系ごとに異なるため、異なる原子種や計算条件で得られた全エネルギーを単純に比較することはできません。

しかし、ある状態から別の状態への変化に伴って状態間のエネルギー差をとることで、基準エネルギーの任意性が取り除かれます。その結果として得られる凝集エネルギーや形成エネルギーといった値は、物理的に意味を持つ量となり、実験値と直接比較することが可能になります。

凝集エネルギーの定義と注意点#

凝集エネルギー ( $E_\text{coh}$ ) は、その物質の結晶状態における1原子あたりの全エネルギー ( $E_\text{bulk}$ ) と、孤立した中性原子状態のエネルギー ( $E_\text{atom}$ )の差として定義されます。

$E_\text{coh} = E_\text{atom} - E_\text{bulk}$

この凝集エネルギーは、より一般的には形成エネルギー (Formation Energy) の一種と見なすことができます。重要なのは、その値がエネルギー差を計算する際の「前後の状態」をどのように定義するかに依存する点です。そのため、計算値と文献値を比較する際には、そのエネルギーがどのような状態を基準に算出されたのかを注意深く確認することが不可欠です。

計算結果と考察#

図1に、Advance/PHASEでGGA-PBE汎関数を用いて計算した50種類以上の元素の凝集エネルギーと、実験値 [1, 2]との比較をパリティプロットで示します。

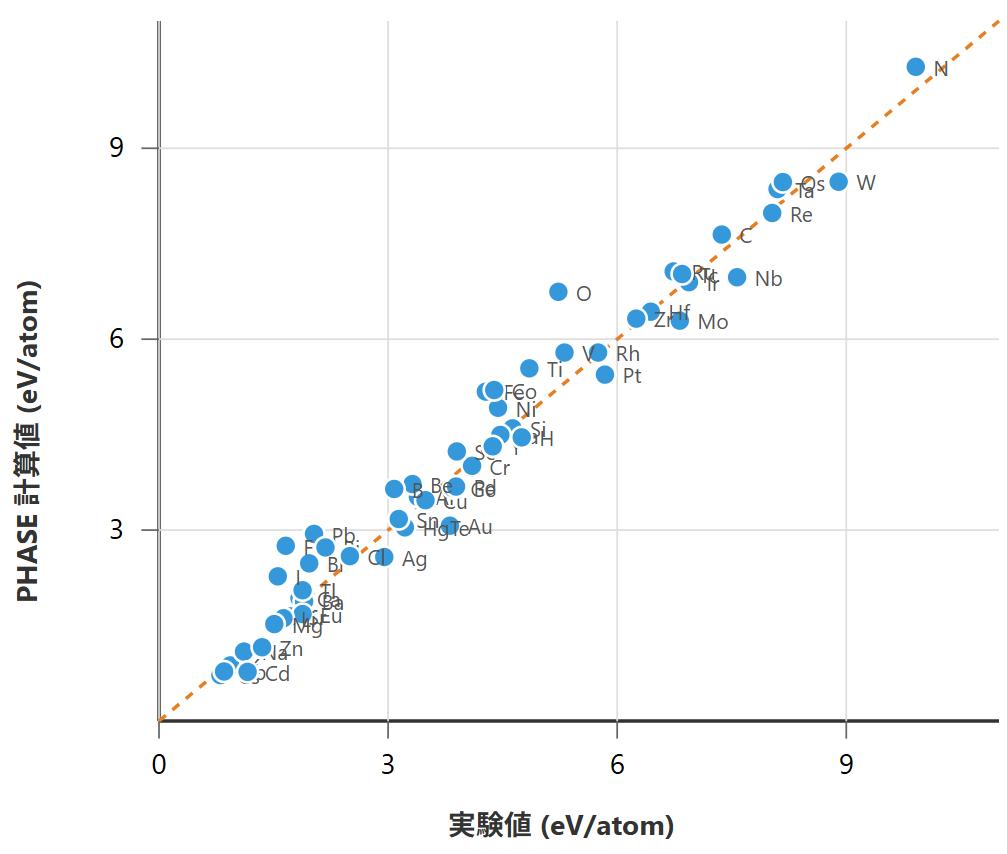
図1. 様々な元素における凝集エネルギーのPHASE計算値と実験値の比較（パリティプロット）

このプロットでは、横軸に実験値、縦軸にPHASEによる計算値をとっています。プロットされた点が対角線（y=x, 図中のオレンジ色の破線）に近ければ近いほど、計算値と実験値が良く一致していることを意味します。

なお、酸素(O)、水素(H)、窒素(N)やハロゲン元素(F, Cl, Br, I)など、安定な二原子分子を形成する元素については、計算の基準が結晶ではなく二原子分子が計算の基準として用いられます。

全体的な傾向: 図1を見ると、プロットされた多くの点が対角線上にきれいに乗っていることがわかります。これは、Advance/PHASEが軽元素から重金属、半導体、ハロゲンに至るまで、多種多様な元素の凝集エネルギーを系統的に、かつ高い精度で再現できることを示しています。
定量的な一致: 例えば、半導体として重要なシリコン(Si)では実験値4.63 eV/atomに対し計算値は4.60 eV/atom、金属の銅(Cu)では実験値3.49 eV/atomに対し計算値は3.47 eV/atomと、非常に良好な一致を示しています。また、凝集エネルギーが非常に大きいタングステン(W)のような元素（実験値8.90 eV/atom, 計算値8.47 eV/atom）でも、その傾向を正しく捉えています。
系統的なずれの考察: 一方で、鉄(Fe)やコバルト(Co)といった3d遷移金属では、計算値が実験値をやや過大評価する傾向が見られます [3]。これは、電子間の相互作用（電子相関）が強い系における密度汎関数理論の一般的な課題の一つですが、それでも全体的な化学的傾向を捉える上では十分に有効です。
酸素について: 酸素ダイマー（O₂）の計算では、分子の特殊な電子状態（三重項状態）が原因で、その凝集エネルギーを過大評価しています。これは、一般的な計算手法（GGA-PBE汎関数など）の課題として広く知られています [4]。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、周期表にわたる様々な元素の凝集エネルギーを計算し、実験値と比較することでその予測精度を検証しました。その結果、計算値は実験値と高い相関を示し、本手法が多様な材料の安定性を評価する上で有効であることが示されました。凝集エネルギーのような「エネルギー差」は、その定義に注意して適切に計算することで、物質科学の様々な場面で定量的な評価を可能にします。

参考文献#

C. Kittel, Introduction to Solid State Physics, 8th ed. (Wiley, 2005).
W. M. Haynes, ed., CRC Handbook of Chemistry and Physics, 97th ed. (CRC Press, 2016).
P. Janthon et al., Journal of Chemical Theory and Computation 10, 3832 (2014).
J. Sun, A. Ruzsinszky, and J. P. Perdew, Physical Review Letters 115, 036402 (2015).