グラフェン単層膜の水素原子透過性: 機械学習NEBを用いた第一原理シミュレーション#

グラフェンは、炭素原子が蜂の巣状に結合したシート状物質であり、その原子1個分の薄さ、優れた機械的強度、高い導電性などから、次世代の電子デバイスやフィルター材料として注目されています。特に、物質の透過を完全に防ぐ「究極の膜」としての性質が知られており、ガスバリア材料や防食コーティングへの応用が期待されています。しかし、この完全な不透過性が全ての原子種に対して成り立つのか、また特定の原子を選択的に透過させることはできないのか、という点は材料設計において極めて重要です。本稿では、第一原理計算ソフトウェアAdvance/PHASEと機械学習NEB(ML-NEB)法を組み合わせ、グラフェン単層膜の水素(H)原子に対する透過性を評価し、その活性化エネルギー障壁を高精度に解析します。
Keywords: 第一原理計算, DFTシミュレーション, グラフェン, 水素透過, 機械学習NEB (ML-NEB), 活性化エネルギー, 遷移状態探索
グラフェンの透過性と遷移状態計算の課題#
グラフェンが多くの気体分子に対して不透過であることは実験的に確認されていますが [1]、最も小さく軽い原子である水素については、理論的な透過エネルギー障壁の報告値に2.4 eVから15 eVまでと大きなばらつきがありました [2]。このばらつきは、反応経路の探索手法の違いに起因すると考えられています。化学反応や物質移動のような素過程の解析では、反応の前後(始状態と終状態)だけでなく、その途中で最もエネルギーが高くなる「遷移状態」を正確に特定することが不可欠です。この遷移状態の(相対)エネルギーが、反応の起こりやすさを決める活性化エネルギー障壁となります。
この遷移状態を探索する代表的な手法がNudged Elastic Band (NEB)法です。NEB法は、始状態と終状態を複数のイメージ(原子構造のコマ撮り)で結び、それらが最小エネルギー経路(MEP)上に来るように最適化する手法です。しかし、従来のNEB法は、全てのイメージに対して繰り返しエネルギーと力の計算を行う必要があり、計算コストが非常に高いという課題がありました。
機械学習NEB (ML-NEB)法による高速化
NEB計算コストの問題を解決するのが、本解析で用いた機械学習NEB(ML-NEB)法 [3]です。ML-NEB法は、ガウス過程回帰(GPR)と呼ばれる機械学習モデルを用いて、ポテンシャルエネルギー曲面(PES)の代理(サロゲート)モデルを構築します。この手法は、第一原理計算の回数を最小限に抑えつつ、高い精度を維持するための巧妙な収束戦略を採用しています。
ML-NEB法の収束プロセス:
- 代理モデルの学習と探索: まず、始状態と終状態などの情報から代理モデルを構築します。次に、モデルの予測に基づき、PESの全体像を把握するために「不確かさが最大」のイメージを優先的に選択し、そのイメージについてのみ第一原理計算を実行してモデルを更新します。この「探索フェーズ」を、反応経路全体の不確かさの最大値が閾値(デフォルト: 0.05 eV)を下回るまで繰り返します。
- 遷移状態の精密化 (CI-NEB): 代理モデルが十分に学習された後、アルゴリズムは「活用フェーズ」に移行します。ここでは、エネルギーが最も高いイメージ(遷移状態の候補)をClimbing Image (CI)として特定し、そのイメージが真の鞍点に収束するように計算を進めます。
- 収束判定: CI-NEBの過程で、遷移状態の候補について第一原理計算を行い、原子に働く力の最大値が収束閾値(デフォルト: 0.05 eV/Å)を下回った時点で計算が終了します。
このように、最終的な収束判断を機械学習モデルではなく第一原理計算で直接行うため、ML-NEB法は計算コストを劇的に削減しながらも、遷移状態を第一原理計算の精度で正しく求めることを保証します。また、ML-NEB法では計算コストがイメージ数にほとんど依存しない点から、十分な数のイメージを使って正確な反応障壁を求めることが可能です。
計算条件とモデル#
本解析の第一原理計算はAdvance/PHASEを使用しました。まず、水素原子が吸着する位置を特定するため、グラフェン表面の代表的な吸着サイト(図1)について安定性を評価しました。その結果、炭素原子の真上であるtopサイトが最も安定であることが分かりました。
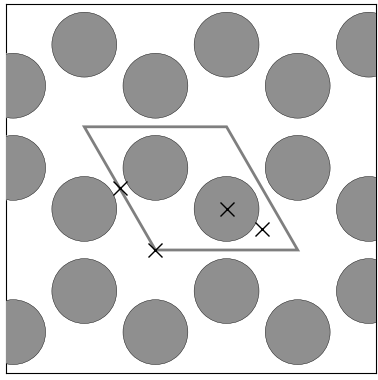
図1. グラフェン表面の主な吸着サイト
x印は、Top(原子の真上)、Bridge(結合の真ん中)、Hollow(六員環の中心)といった代表的な吸着位置を示します。
この結果に基づき、水素原子がtopサイトに吸着した状態(図2)を始状態、グラフェンを透過して反対側のtopサイトに吸着した状態を終状態として、ML-NEB法による透過経路の探索を行いました。中間イメージ数を十分な数である17個にしました。詳細な計算条件を表1にまとめます。
表1. 計算条件
| 項目 | 設定 |
|---|---|
| 交換相関汎関数 | GGA (PBE) |
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル (H: ノルム保存) |
| スーパーセル | グラフェン 4x4x1 スーパーセル |
| k点サンプリング | 3x3x1 |
| スピン分極 | 考慮あり |
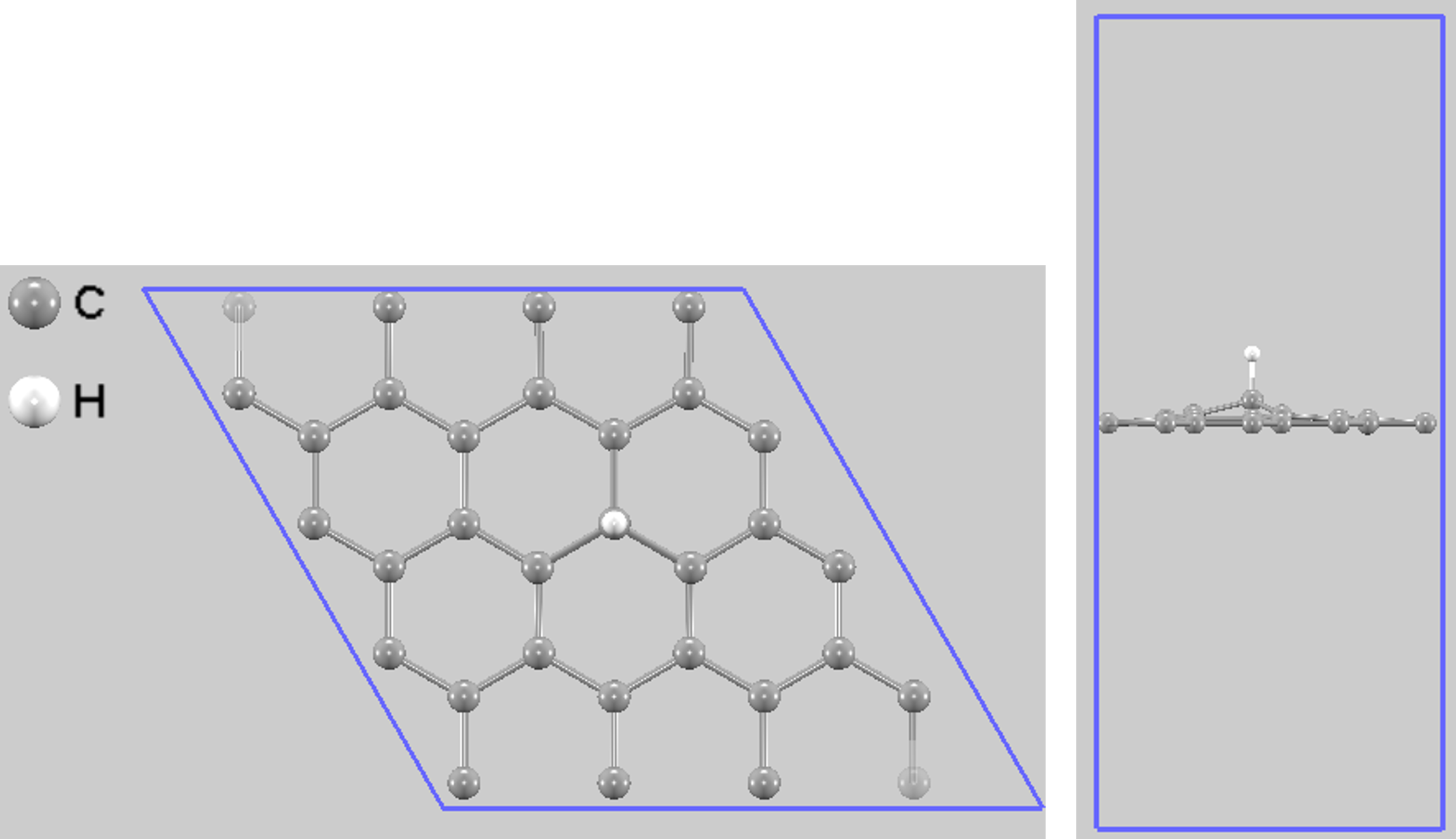
図2. 水素原子の最安定吸着位置(上面図および側面図)
水素原子(白)は炭素原子(灰)の真上(topサイト)に吸着し、結合した炭素原子がグラフェン平面からわずかに突き出ます。透明な原子(左上と右下のC原子、2個)は計算中に固定されています(スーパーセル全体の並進を防ぎ、計算を安定させるため)。
計算結果と考察#
ML-NEB法の収束過程#
ML-NEB法の計算がどのように進行し、遷移状態へと収束していくのかを理解するために、計算ステップごとのエネルギーと力の変化を見てみましょう。図3と図4は、ML-NEB法が評価した各構造(ステップ)におけるエネルギーと最大力の推移を示しています。
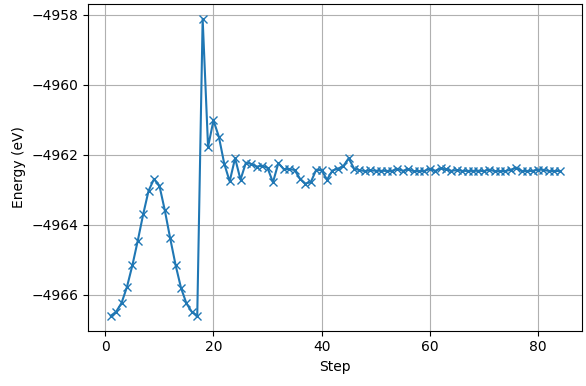
図3. 計算ステップごとのエネルギー変化
初期段階ではエネルギーが大きく変動し、広範囲のエネルギー空間を探索している様子がわかります。ステップが進むにつれて、遷移状態近傍のエネルギー値に収束していきます。
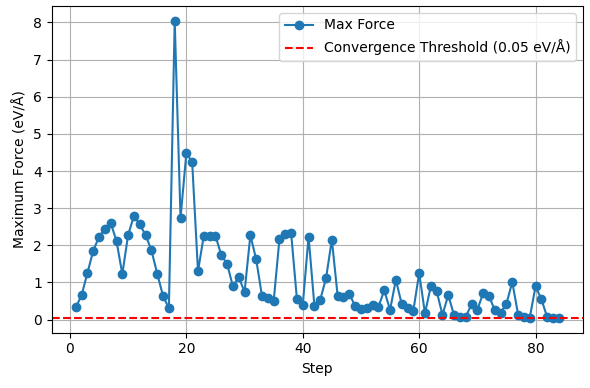
図4. 原子に働く力の最大値の推移
「探索フェーズ」における力の急上昇が見られますが、ステップが進むにつれて、変動を伴う減少傾向を示し、最終的に収束閾値(赤点線、0.05 eV/Å)を下回っています。
図3を見ると、計算の初期段階では評価される構造のエネルギーが大きく変動していることがわかります。これは、機械学習モデルがポテンシャルエネルギー曲面の全体像を把握するために、積極的に未知の領域を探索している「探索フェーズ」に相当します。計算が進むにつれてエネルギーの変動は小さくなり、遷移状態のエネルギーに近づいていく「活用フェーズ」へと移行します。図4は、原子に働く力の最大値の推移を示しています。計算の初期段階では力が大きく変動していますが、ステップが進むにつれて全体としては減少傾向にあり、最終的に収束閾値(赤点線、0.05 eV/Å)を下回っていることから、計算が正しく遷移状態に収束したことが確認できます。これらのグラフは、ML-NEB法が効率的にエネルギー曲面を学習し、自動的に遷移状態へと収束する過程を可視化したものであり、本手法の強力さを示しています。
水素透過のエネルギー障壁#
ML-NEB法を用いて計算した、水素原子がグラフェンを透過する際の最終的なエネルギー変化のプロファイルを図5に示します。
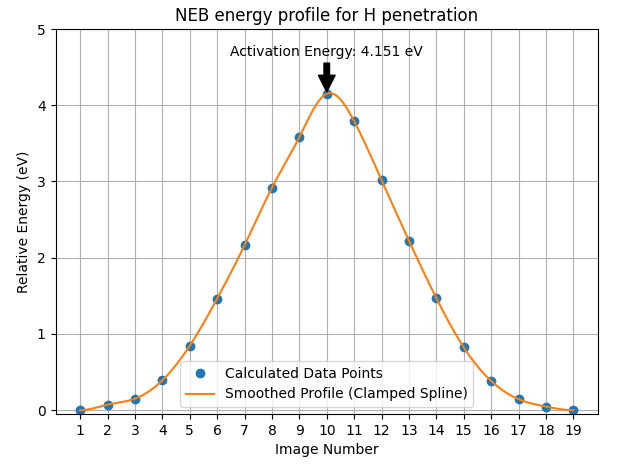
図5. 水素原子がグラフェンを透過する際の最小エネルギー経路
横軸は反応経路に沿ったイメージ番号、縦軸は始状態を基準とした相対エネルギーを示します。計算されたデータ点(青丸)とその点をスプライン補間で滑らかに結んだプロファイル(オレンジ線)から、活性化エネルギーは4.151 eVと算出されました。
計算の結果、水素原子がグラフェン単層膜を透過する際の活性化エネルギー障壁は 4.151 eV と算出されました。この値は、先行研究 [2] で報告されている4.2 eVという値と非常によく一致しており、本シミュレーションの妥当性を示しています。このエネルギー障壁は非常に高く、通常の温度条件下では水素原子が欠陥のないグラフェンを透過することは極めて困難であることを示唆しています。物理的には、グラフェンの非常に強固な結合ネットワークと安定した電子状態を乱すには、大きなエネルギーが必要と考えられます。
エネルギープロファイルの頂点に相当する遷移状態の構造を図6に示します。遷移状態では、水素原子がグラフェンを構成する六員環の中心付近に位置しています。水素とcarbon pairの距離が約1.28 Å, 第2近接のC原子との距離は約1.47 Åであり、先行研究 [2] とよく一致しています。
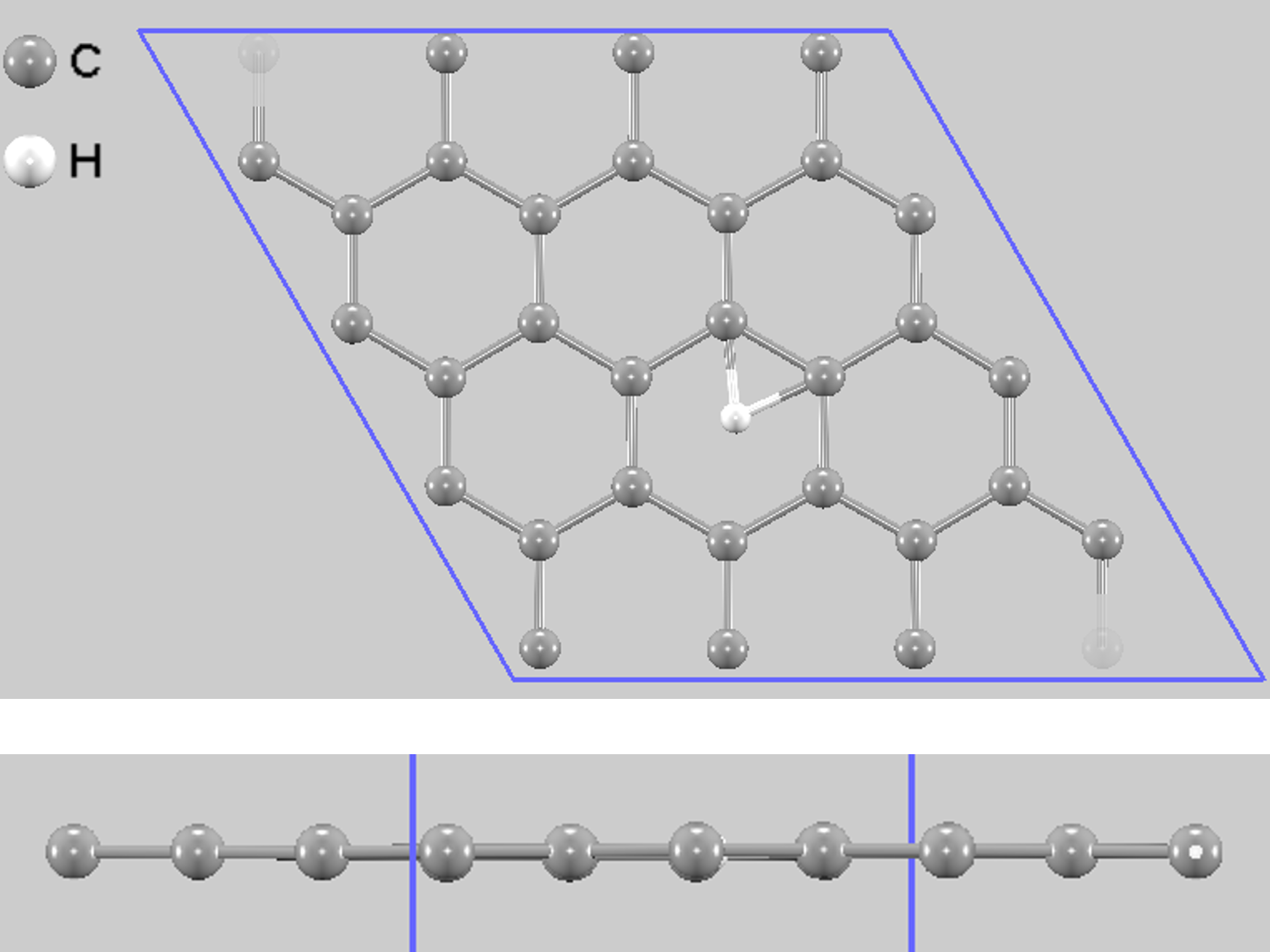
図6. 遷移状態の原子構造
水素原子(白)が六員環の中心付近を通過します。すべての原子が同じ平面に位置します。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEと機械学習NEB法を組み合わせることで、グラフェン単層膜の水素原子透過における活性化エネルギー障壁を高精度かつ効率的に算出しました。得られた活性化エネルギー 4.151 eV は、先行研究とよく一致し、欠陥のないグラフェンが水素に対して極めて高いバリア特性を持つことを理論的に裏付けました。また、収束過程の解析を通じて、ML-NEB法が効率的にエネルギー曲面を学習し、自動的に遷移状態へと収束する様子を明らかにしました。これは、ML-NEB法が複雑な反応経路の探索において、計算コストを大幅に削減しつつも、高い精度を維持できる強力なツールであることを示しています。このような計算科学的アプローチは、新しいフィルター材料やバリア膜の設計・開発において、原子レベルの知見に基づいた信頼性の高い指針を提供します。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- V. Berry, "Impermeability of graphene and its applications", Carbon 62, 1 (2013).
- L. Tsetseris and S. T. Pantelides, "Graphene: An impermeable or selectively permeable membrane for atomic species?", Carbon 67, 58 (2014).
- J. A. Garrido Torres, P. C. Jennings, M. H. Hansen, J. R. Boes, and T. Bligaard, "Low-scaling algorithm for nudged elastic band calculations using a surrogate machine learning model", Phys. Rev. Lett. 122, 156001 (2019).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学