電気化学的アンモニア合成における窒素還元触媒の活性・選択性の第一原理解析#

PHASE logo

電気化学的アンモニア合成は、持続可能な社会の実現に向けた重要な技術の一つです。この反応の鍵を握るのが、窒素還元反応（NRR）を効率的に進行させる電極触媒です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、密度汎関数法(DFT)に基づいて、いくつかの遷移金属（Re, Ru, Pt, Cu, Au）の表面上でのNRRを解析しました。具体的には、窒素原子の吸着Gibbs自由エネルギー( $\Delta G_{\text{N}^*}$ )を単一の記述子（Descriptor）として採用し、この記述子とNRR自体の触媒活性および競合反応である水素発生反応（HER）の触媒活性を比較することで、これらの金属群の触媒活性トレンドと、実用化に向けた最大の課題である「選択性」について議論します。

Keywords: 第一原理計算, 密度汎関数法(DFT), 窒素還元反応(NRR), 電気化学的アンモニア合成, 記述子(Descriptor), Gibbs自由エネルギー, Volcano plot, 選択性, 水素発生反応(HER)

記述子の決定と計算方法#

触媒活性を効率的に議論する上で、複雑な反応経路を代表する単一のパラメータ（記述子）を決定することが重要です。NRRは多くの中間体（*N₂H, *NH, *NH₂など）が関与しますが、本解析では文献[1] に倣い、最も基本的な構成要素である窒素原子の吸着Gibbs自由エネルギー $\Delta G_{\text{N}^*}$ を記述子として採用しました。

$\Delta G_{\text{N}^*}$ は、気相のN₂分子が表面に吸着して窒素原子（N*）となる以下の反応のGibbs自由エネルギー変化として定義されます。

$\dfrac{1}{2} \text{N}_{2}(\text{g}) + * \rightarrow \text{N}^*$

Gibbs自由エネルギー（ $\Delta G$ ）は、DFT計算で得られる反応エネルギー（ $\Delta E$ ）に対し、ゼロ点エネルギー（ $\Delta E_{\text{ZPE}}$ ）とエントロピー（ $-T\Delta S$ ）の補正を加えることで算出されます。

$\Delta G = \Delta E + \Delta E_{\text{ZPE}} - T\Delta S$

本解析で用いる $\Delta G_{\text{N}^*}$ の計算式は以下の通りです。

$\Delta G_{\text{N}^*} = \Delta E_{\text{N}^*} + 0.26 \text{ eV}$

$\Delta E_{\text{N}^*} = E_{\text{N*}} - E_* - \dfrac{1}{2}E_{\text{N}_{2}(\text{g})}$

ここで、 $\Delta E_{\text{N}^*}$ はDFT計算から直接得られる吸着エネルギーであり、0.26 eVは $\Delta E_{\text{ZPE}} - T\Delta S$ の補正項に相当します。この補正値は、厳密には吸着する金属表面の種類によって変動しますが、本解析では金属によらず一定であると近似しています。この近似の妥当性は以下のように説明できます。

エントロピー項 ( $-T\Delta S$ ): $\Delta S = S_{\text{N}^*} - \frac{1}{2} S_{\text{N}_2(\text{g})}$ 。気相のN₂分子は並進・回転の自由度を持つためエントロピー（ $S_{\text{N}_2(\text{g})}$ ）が非常に大きいのに対し、表面に化学結合で固定された吸着N原子（N*）のエントロピー（ $S_{\text{N}^*}$ ）はほぼゼロとみなせます。したがって、 $\Delta S$ は主に金属種に依存しない物理定数 $S_{\text{N}_2(\text{g})}$ によって決まり、エントロピー補正（ $-T\Delta S$ ）は金属によらずほぼ一定となります。
ゼロ点エネルギー項 ( $\Delta E_{\text{ZPE}}$ ): $\Delta E_{\text{ZPE}} = E_{\text{ZPE}, \text{N}^*} - \frac{1}{2} E_{\text{ZPE}, \text{N}_2(\text{g})}$ 。このうち $E_{\text{ZPE}, \text{N}^*}$ はN原子と金属表面との結合強度に依存するため、厳密には金属種によって変動します。しかし、触媒活性のトレンドを支配する吸着エネルギー $\Delta E_{\text{N}^*}$ の変動幅（金属種によって数 eV にも達する）と比較すると、 $\Delta E_{\text{ZPE}}$ の変動幅（0.1 eV 程度）は非常に小さいと予想されます。

したがって、触媒活性の全体的な傾向を議論する上では、計算コストのかかる補正値の個別計算を省略し、文献 [1] で算出された一定値（0.26 eV）を用いることは妥当な近似であると言えます。

計算モデルと計算条件#

本解析では、fcc（面心立方）金属である Pt, Cu, Au の最密充填面(111)面と、hcp（六方最密充填）金属である Re, Ru の最密充填面(0001)面を計算対象としました。窒素原子（N）の吸着サイトとして、これらの表面における高対称性サイト（top/bridge/hollowサイト）を考慮しました。

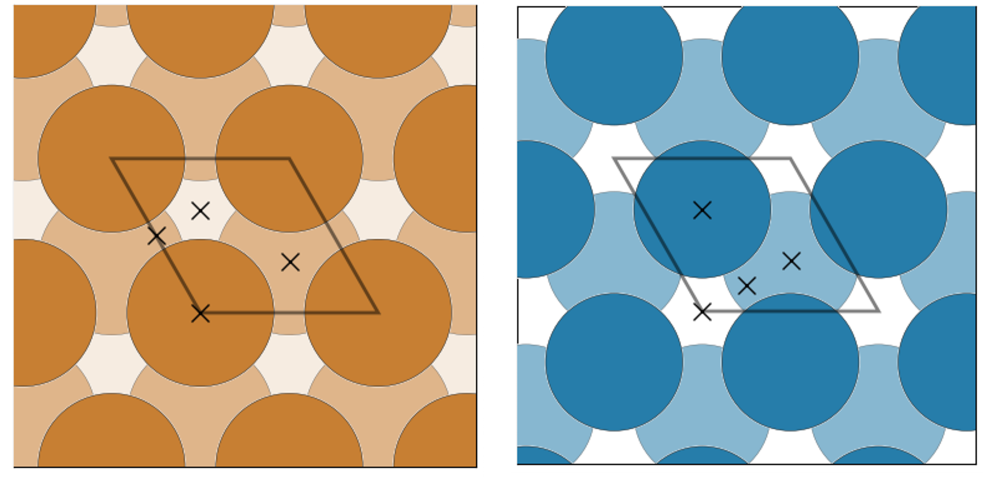
fcc(111)とhcp(0001)面の高対称性吸着サイト
図1. (左) fcc金属(111)面、(右) hcp金属(0001)面。 ×で示す高対称性吸着サイト: top, bridge, hcp-hollow, fcc-hollow サイト。

本解析で用いた主な計算条件は表1に示されています。

表1. 計算条件の概要

項目	設定
擬ポテンシャル	ウルトラソフト
交換相関汎関数	RPBE
波動関数のカットオフエネルギー	25 ～ 50 Rydberg
表面スーパーセル	2x2
原子層	3層（底面2層固定）
表面被覆率	0.25
真空層	10 Å

計算結果と考察#

格子定数の最適化#

表面スラブモデルを構築する前に、RPBE交換相関汎関数を用いて各金属バルクの格子定数を最適化しました。RPBEは吸着エネルギーの計算に適していますが、格子定数がPBE汎関数よりも過大に評価される傾向があります。本解析では一貫性を保つため、スラブモデルの格子定数としてRPBEで最適化した値を使用しました。図2および図3に、fcc Cuとhcp ReのE-V（エネルギー-体積）曲線（Equation of State, EOS）のフィッティング結果を示します。

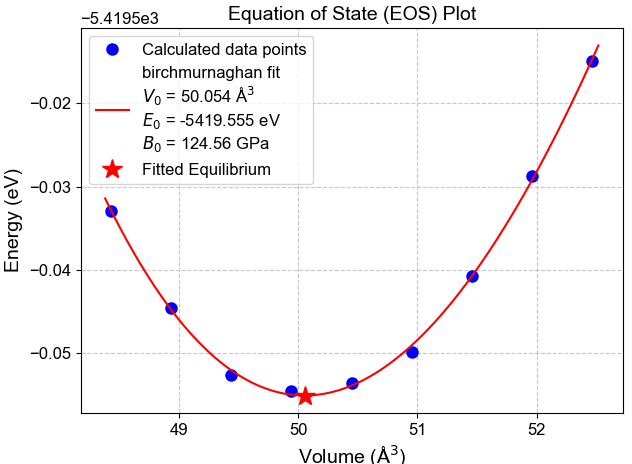
図2. fcc Cu の E-V曲線 (RPBE)。Vは慣用 (conventional)単位格子当たりの体積。Birch-Murnaghanの式でフィッティングした結果、平衡格子定数として 3.685 Å が得られました。

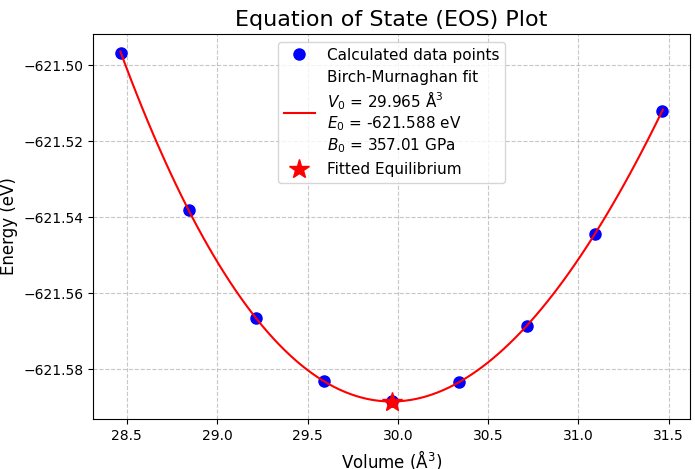
hcp Re の E-V曲線 (RPBE)
図3. hcp Re の E-V曲線 (RPBE, at optimal c/a)。Vは基本(primitive)単位格子当たりの体積。平衡格子定数として a = 2.777 Å, c = 4.487 Å が得られました。

最安定吸着サイト#

次に、各金属表面の高対称性サイト（図1）に窒素原子を吸着させ、構造最適化計算を行いました。その結果、0.25の被覆率において、fcc(111)面（Pt, Cu, Au）ではfcc hollowサイト、hcp(0001)面（Re, Ru）ではhcp hollowサイトが、それぞれ窒素原子の最安定な吸着サイトであることが分かりました。図4にCu(111)とRe(0001)における最安定吸着構造の例を示します。

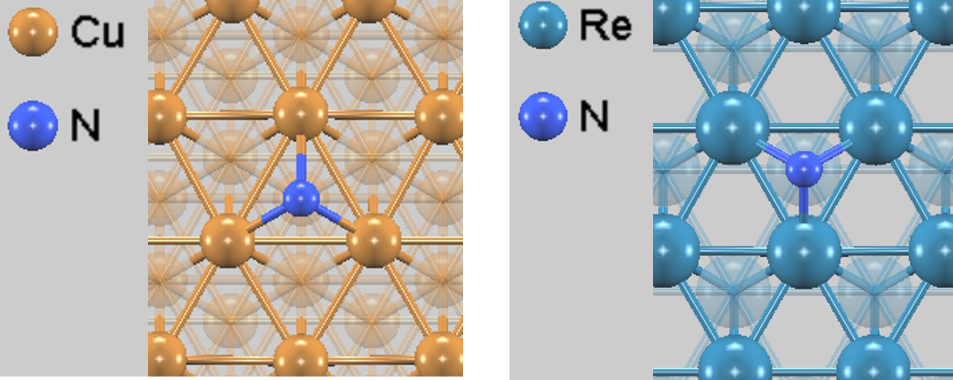
Cu(111)のfcc hollowサイトとRe(0001)のhcp hollowサイトへのN吸着
図4. (左) Cu(111)における最安定窒素吸着サイト (fcc hollow)。(右) Re(0001)における最安定窒素吸着サイト (hcp hollow)。いずれも上面図であり、固定層の原子は半透明で表示されています。

窒素吸着エネルギーと文献値の比較#

各金属の最安定サイトにおける窒素吸着エネルギー（ $\Delta E$ ）を算出し、それと補正値（0.26 eV）を用いて吸着Gibbs自由エネルギー（ $\Delta G$ ）を求めました。これらの結果を、文献値と比較して表2にまとめます。

表2. 窒素吸着（自由）エネルギーの計算結果と文献値の比較 (単位: eV)

Metal	$\Delta E$ 計算値	$\Delta E$ 文献値	$\Delta G$ 計算値	$\Delta G$ 文献値
Re	-1.41	-1.415^a, -1.47	-1.15	-1.23
Ru	-0.54	-0.29^b, -0.02	-0.28	-0.34
Pt	0.71	0.75	0.97	0.97
Cu	1.67	1.65	1.93	1.76
Au	2.83	2.79	3.09	3.15

a: 文献[2] (RPBE), b: 文献[3] (RPBE)
$\Delta E$文献値(その他)は文献[1] (RPBE)
$\Delta G$文献値は文献[4] (BEEF-vdW)

表2から、Ruを除く全ての金属において、本計算で得られた吸着エネルギー（ $\Delta E$ 計算値）は、同じRPBE汎関数を用いた文献値とよく一致していることが分かります。Ru(0001)面での窒素吸着エネルギーについては、文献[1]の-0.02 eV以外、文献[3]の-0.29 eV (RPBE)、さらに文献[5]の-0.77 eV (PW91) など、計算手法によって様々な値が報告されており、Ru表面の計算が条件に依存しやすいことが考えられます。
興味深いことに、記述子である $\Delta G$ 計算値（RPBE）は、Cuで0.17 eVの差があるものの、他の金属（Re, Ru, Pt, Au）では、異なる汎関数（BEEF-vdW）を用いて計算された $\Delta G$ 文献値と全体的に良く一致しています。

触媒活性のトレンド (Volcano Plot)#

得られた $\Delta G_{\text{N}^*}$ （ $\Delta G$ 計算値）を記述子として横軸にとり、触媒活性の指標である限界電位（Limiting Potential, $U_L$ ） [4] を縦軸にプロットしました（図5）。限界電位 $U_L$ は、反応経路全体が発エルゴン的（ $\Delta G < 0$ ）になるために必要な最小の電位であり、この値が0 Vに近い（負に小さい）ほど高性能な触媒であることを示します。この種のプロットは、触媒化学におけるサバティエの原理（Sabatier's Principle）を示す典型的なボルケーノ（火山型）プロットと呼ばれます。

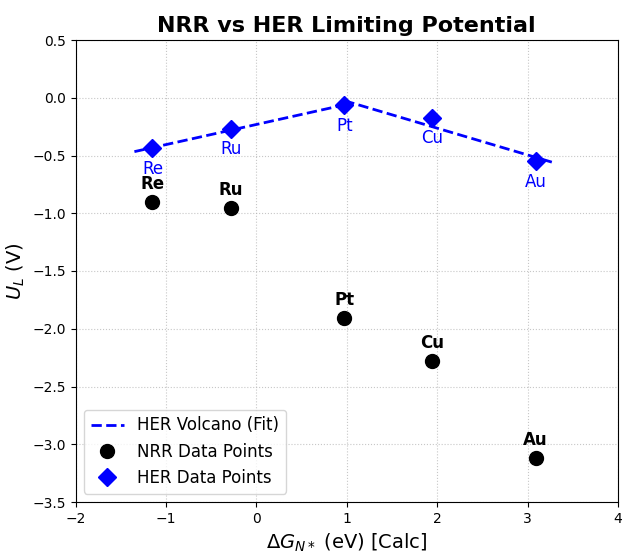
NRR vs HER Limiting Potential Volcano Plot
図5. NRRとHERの限界電位（ $U_L$ ）と窒素吸着Gibbs自由エネルギー（ $\Delta G_{\text{N}^*}$ ）の関係（Volcano Plot）。NRRのデータ（黒丸）とHERのデータ（青菱形、文献[4]）をプロットしています。

図5のNRRデータ（黒丸）を見ると、ボルケーノプロットの形状が確認できます。

弱吸着側 (右側: Pt, Cu, Au): $\Delta G_{\text{N}^*}$ が正に大きく、窒素の吸着が弱い領域です。この領域では、最初のN₂の活性化が困難（律速段階）となります。吸着が強くなる（ $\Delta G_{\text{N}^*}$ が小さくなる）ほど活性（ $U_L$ ）が向上します。
強吸着側 (左側: Re, Ru): $\Delta G_{\text{N}^*}$ が負に大きく、窒素の吸着が強い領域です。この領域では、吸着した中間体（*NH₂など）の脱離が困難（律速段階）となります。吸着が弱くなる（ $\Delta G_{\text{N}^*}$ が大きくなる）ほど活性が向上します。

この解析から、ReとRuはボルケーノの頂点付近に位置しており、今回調査した金属の中では、NRRの「活性」自体はPt, Cu, Auよりも高いことが示唆されます。

競合反応（HER）との選択性#

最後に、NRR触媒開発における最大の課題である「選択性」について議論します。水溶液中でNRRを起こすために負の電位を印加すると、プロトンの還元による水素発生反応（HER）が必ず競合反応として起こります。

NRR:　　　N₂ + 6H⁺ + 6e^- → 2NH₃

HER:　　　2H⁺ + 2e^- → H₂

図5には、NRR（黒丸）と同時にHERの限界電位（青菱形）もプロットされています。NRRを進行させるためには、少なくとも $U_L(\text{NRR})$ （黒丸の値）までの負電位が必要ですが、HERはそれよりも大幅に正の電位である $U_L(\text{HER})$ （青菱形の値）で進行してしまいます。この傾向は、Re, Ru, Pt, Cu, Auの全ての金属において、同様な結果が示されました。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Re, Ru, Pt, Cu, Auの最密充填面における電気化学的窒素還元反応（NRR）の触媒活性と選択性を、密度汎関数法（DFT）に基づいて理論的に評価しました。窒素原子の吸着Gibbs自由エネルギー（ $\Delta G_{\text{N}^*}$ ）を記述子として用いたVolcano Plot解析により、今回調査した金属群の中ではReとRuが最も高いNRR「活性」（最も0 Vに近い限界電位）を持つことが示唆されました。しかし、実用上の最大の課題である競合反応（HER）との選択性を比較した結果、今回調査した全ての清浄な金属表面（fcc(111)面、hcp(0001)面）において、HERがNRRよりも圧倒的に有利（限界電位がより0 Vに近い）であることが明らかになりました。この結果は、これらの金属表面がNRRに対して選択的ではなく、印加した電流のほぼ全てがHERに使われてしまうことを示唆しており、高効率なNRR触媒の開発には、HERを抑制しつつNRR活性を高めるための更なる材料設計が必要であることを示しています。本解析で用いたような第一原理計算（理論）と、実際の触媒合成・評価（実験）を緊密に連携させるアプローチは、近年高性能な電極触媒の開発において成功を収めている手法です [6]。

参考文献#

E. Skulason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónssona, and J. K. Nørskov, "A theoretical evaluation of possible transition metal electro-catalysts for N2 reduction", Phys. Chem. Chem. Phys. 14, 1235 (2012).
K. Hahn and M. Mavrikakis, "Atomic and molecular adsorption on Re(0001)", Topics in Catalysis 57, 54 (2014).
L. Diekhöner, A. Baurichter, H. Mortensen, and A. C. Luntz, "Observation of metastable atomic nitrogen adsorbed on Ru(0001)", J. Chem. Phys. 112, 2507 (2000).
J. H. Montoya, C. Tsai, A. Vojvodic, and J. K. Nørskov, "The challenge of electrochemical ammonia synthesis: a new perspective on the role of nitrogen scaling relations", ChemSusChem, 8, 2180 (2015).
J. J. Mortensen, Y. Morikawa, B. Hammer, and J. K. Nørskov, "Density functional calculations of N₂ adsorption and dissociation on a Ru(0001) surface", J. Catal. 169, 85 (1997).
Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov, and T. F. Jaramillo, "Combining theory and experiment in electrocatalysis: Insights into materials design", Science 355, eaad4998 (2017).