Blue moon法による自由エネルギー障壁の評価#

拘束条件付き構造緩和の概念を、有限温度下での分子動力学シミュレーションに応用した手法がblue moon法です。この手法を用いることで、ある状態から別の状態へ遷移する際の自由エネルギー変化を算出することができます。ここでは、第一原理計算ソフトウェアAdvance/PHASEに実装されたblue moon法を用いて自由エネルギー障壁の計算事例を紹介します。
Keywords: first-principles calculation, chemical reaction, constrained molecular dynamics, blue moon method
Blue moon法の概要#
Blue moon法 [1-3] は、ある反応座標(Reaction Coordinate, RC) に沿った自由エネルギープロファイル(Potential of Mean Force, PMF)を計算するための代表的な手法です。PMFは、化学反応や分子のコンフォメーション変化などの素過程を理解する上で非常に重要です。
この手法の核心は、「力を積分するとエネルギーが得られる」という物理学の基本原理を、統計力学的な自由エネルギー計算に応用する点にあります。
理論形式 (Formalism)#
まず、反応座標 の関数としてのヘルムホルツ自由エネルギー (これがPMFです)を考えます。熱力学によれば、ポテンシャル(エネルギー)の傾き(微分)は力に相当します。同様に、PMFの傾きは、その反応座標の点で系にはたらく平均力(Mean Force) となります。数式で表すと以下の関係が成り立ちます。
この関係から、もし各点 での平均力 を計算できれば、それを反応座標に沿って積分することで、2点間の自由エネルギー差 を求めることができます。
Blue moon法の独創性は、平均力を拘束分子動力学(Constrained MD)シミュレーションから算出する点にあります。
シミュレーションにおいて、反応座標 が特定の値 を取るように、系に拘束(constraint)をかけます。この拘束を維持するためには、仮想的な「力」を系に加える必要があります。この力は、ラグランジュの未定乗数法におけるラグランジュ乗数 として計算されます。
Blue moon法の理論によれば、求めたい平均力 は、このシミュレーションで得られるラグランジュ乗数 のアンサンブル平均 と直接関係づけられます。
厳密な表式には反応座標の定義に依存する補正項が含まれますが、中心的なアイデアは次の通りです。
ここで、 は、反応座標を に固定した状態でのアンサンブル平均を意味します。この拘束力と補正項を合わせたものが、真の平均力 となります。
計算手順のまとめ#
Blue moon法によるPMF計算は、以下のステップで進められます。
- 反応座標の定義: 興味のある現象(例:分子の解離)に対応する反応座標 (例:2原子間距離)を定義します。
- サンプリング点の分割: 計算したい反応座標の範囲(例: から まで)を、複数の点に分割します(例: ごとに )。
- 拘束MDの実行: 分割した各点 で、反応座標の値をその点に固定した拘束MDシミュレーションを実行します。
- 平均拘束力の算出: 各シミュレーションから、拘束を維持するために必要な力(ラグランジュ乗数 )の時系列データを取得し、その時間平均 と補正項を計算して、平均力 を求めます。
- 熱力学積分: すべての点 で得られた平均力 を、反応座標に沿って数値積分します。
これにより、反応経路全体の自由エネルギープロファイル が再構築されます。このように、blue moon法は、一連の拘束シミュレーションから得られる「拘束力」を積分するという、直感的で強力なアプローチによって自由エネルギー地形を明らかにする手法です。
Advance/PHASEには、blue moon法に対応したGUIが設けられているため、上記の計算手順をスムーズに実行できます。図1に、blue moon法を使用する際の設定画面および結果解析のスナップショットを示します。
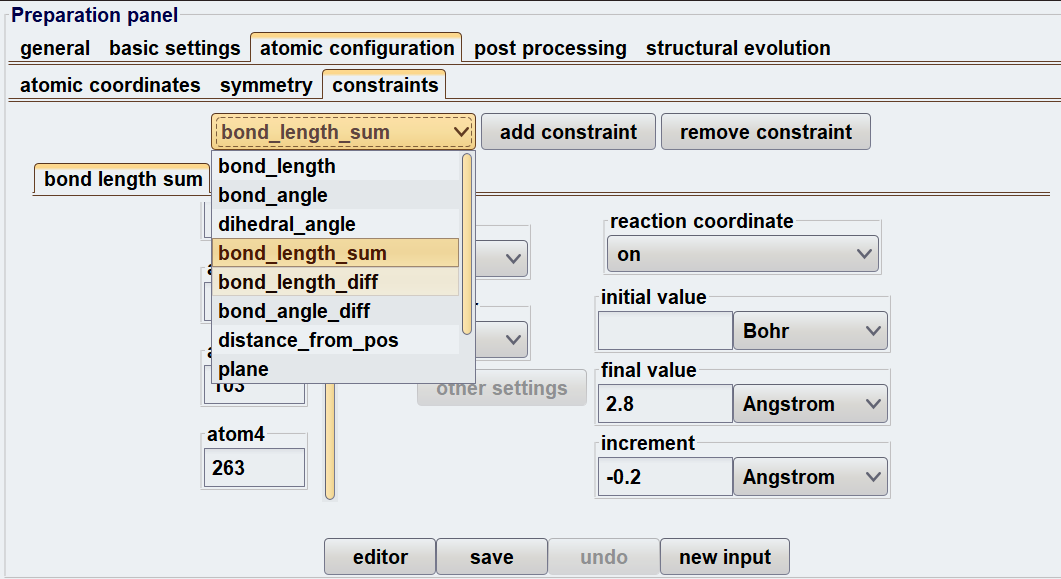
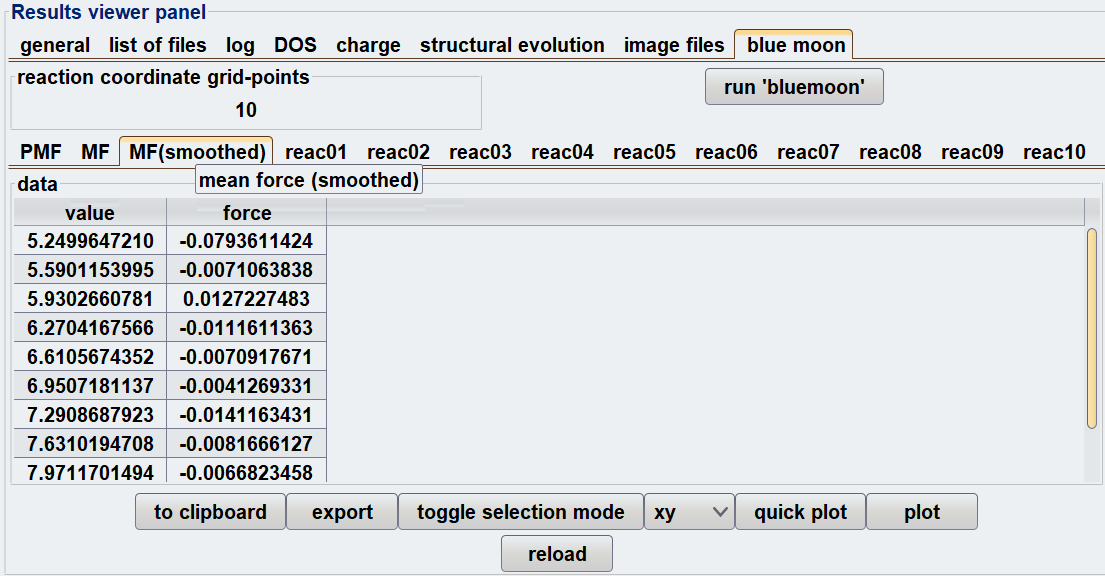
図1.Blue moon法使用時のGUI画面: (上)入力設定 (下)結果解析
Blue moon法の特徴#
Blue moon法を採用する大きな利点として、有限温度の自由エネルギー差が、理論的に厳密な形で得られる、という点が挙げられます。また、単なる構造最適化やNEB法と違い実際の有限温度のダイナミクスを追跡するので、たとえば溶液中の反応なども扱える点も利点であると言えます。また、並列化は容易であり、その並列化効率も良好です。他方、「検討したい各反応座標」において、「十分な統計精度の得られる回数」の分子動力学シミュレーションを実行する必要があるので、その計算量は膨大であると言えます。また、「反応座標を拘束した構造最適化」と同様に、事前に想定した反応座標および反応経路が、対象とする現象の本質を十分に反映していない限り意味のある解を得ることはできません。
計算事例#
H2O2分子の回転障壁#
計算条件#
計算は、10 Å×10 Å×10 Å の単位胞にH2O2分子を1 つ置いた系で行いました。カットオフエネルギーは、波動関数に対しては25 Rydberg、電荷密度については225 Rydberg としました。k 点サンプリングはΓ点のみを採用しました。回転障壁の評価のため、2面角を1°から171°まで10°きざみで変化させ、各点において2面角を拘束しました。各反応座標につき、時間刻み0.7 fsで2,000回の拘束条件付き分子動力学シミュレーションを温度10Kで実行しました。はじめの1,000回は平衡化に要したとみなし、後半の1,000回のデータによって自由エネルギー差の計算を実行しました。
計算結果#
この計算によって得られた自由エネルギー差を図2に紹介します。図2には、比較のため拘束条件付き構造最適化によって得られた結果も併せて表示しています。Blue moon法においてはあくまで自由エネルギーの差しか求められないので、異なるシミュレーションの比較を行う場合は何らかの合理的な原点の決め方を採用する必要があります。そこで、ここではエネルギーの原点として2面角0 radianの値を利用しました。
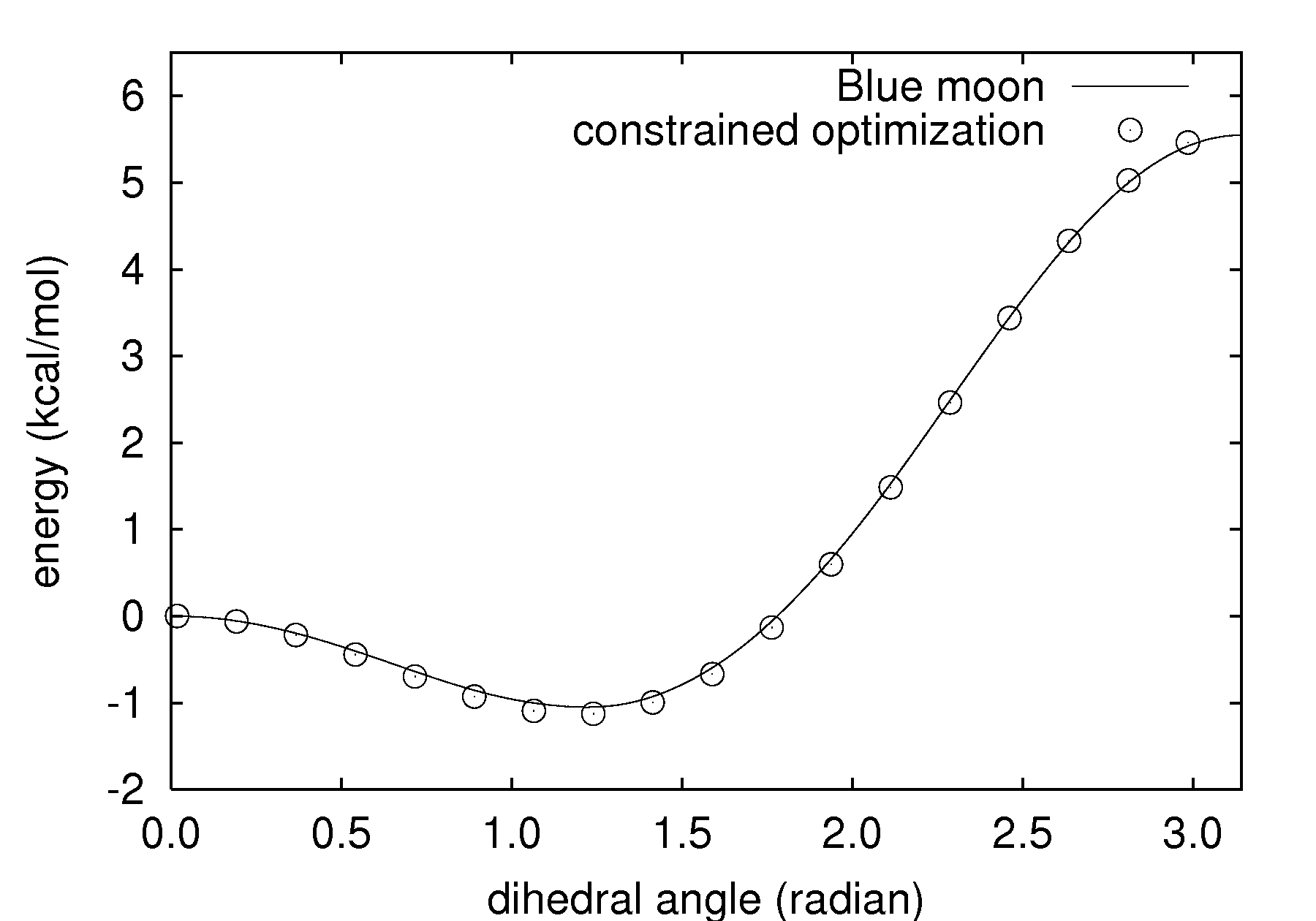
図2.実線:Blue moon法によって得られた自由エネルギー差、白丸:拘束条件付き構造最適化によって得られたエネルギー。
図2より、2つの手法によってほぼ同じ結果が得られていることがわかります。4原子分子の2面角周りの回転ポテンシャルは温度の影響はほとんど受けないと予想されます。実際、温度300Kのシミュレーションからもほぼ同じ結果が得られることを確認しています。したがって、ここで得られた結果は妥当なものであると考えられます。
水中におけるアルカリ-ハライドの解離#
水の中で岩塩などのアルカリ-ハライドが溶解する現象は極めて身近な現象ですが、その原子レベルでの理解は充分であるとは言えません。ここでは、水の中で塩化ナトリウム(NaCl)分子が解離するために必要な自由エネルギーを計算し、NaClがどのように解離していくかを調べた解析例を紹介します。
アルカリハライドが解離する際には、次のような過程を経ると言われています。
Contact Ion Pair (CIP) ⇔ Solvent Separated Ion Pair (SSIP) ⇔ Free Ions (FI)
Contact Ion Pair (CIP)とは、アニオン原子とカチオン原子は隣接し、カチオン原子の周りにはアニオン原子と水分子の酸素原子が、アニオン原子の周りにはカチオン原子と水分子の水素原子が存在するような構造をとる状態のことです。カチオン原子-アニオン原子間の距離が離れていくと、間に水分子が入り込み、カチオン原子-水分子-アニオン原子という、比較的複雑な複合体が安定に存在すると考えられています。これを、Solvent Separated Ion Pair (SSIP)と呼びます。CIPとSSIPの間にはある程度の障壁エネルギーが存在します。すなわち、CIPからSSIPへ至る過程はactivated processであると考えられています。アニオン原子とカチオン原子間の距離がさらに離れていくと、カチオン原子とアニオン原子のダイナミクスはほぼ相関が無くなり、Free Ionsとなります。ここでは、このような解離の過程を、アニオン原子-カチオン原子間の距離を拘束した分子動力学シミュレーションを実施することによって解析します。
計算条件#
計算は、64個の水分子にNaとClのペアを1つずつ配置した系で行いました。単位胞は、一辺あたり12.416 Åの立方体を採用しました。k点サンプリングはΓ点のみとしました。カットオフエネルギーは、これまでと同様波動関数、電荷密度に対してそれぞれ25 Rydberg、 225 Rydbergとしました。初期の原子配置は古典分子動力学シミュレーションの結果を、第一原理分子動力学シミュレーションを2 psほど走らせることによって作成しました。反応座標はNaとCl間の距離とし、2.4 Åからはじめて0.2 Åきざみで6.2 Åまで変化させました(これよりも長い距離とするとセル一辺の半分の長さを超えてしまい、拘束条件に望まれないバイアスがかかってしまいます)。時間刻みは0.7 fsとしました。各反応座標においては6,000ステップの分子動力学シミュレーションを、温度300Kで行いました。自由エネルギー計算の際には、はじめの1,000ステップのデータは平衡化に要したとみなし利用しませんでした。
Na-Cl間距離と自由エネルギーの関係#
本計算によって得られるカチオン原子―アニオン原子間の距離と自由エネルギー差の関係を、図3に示します。
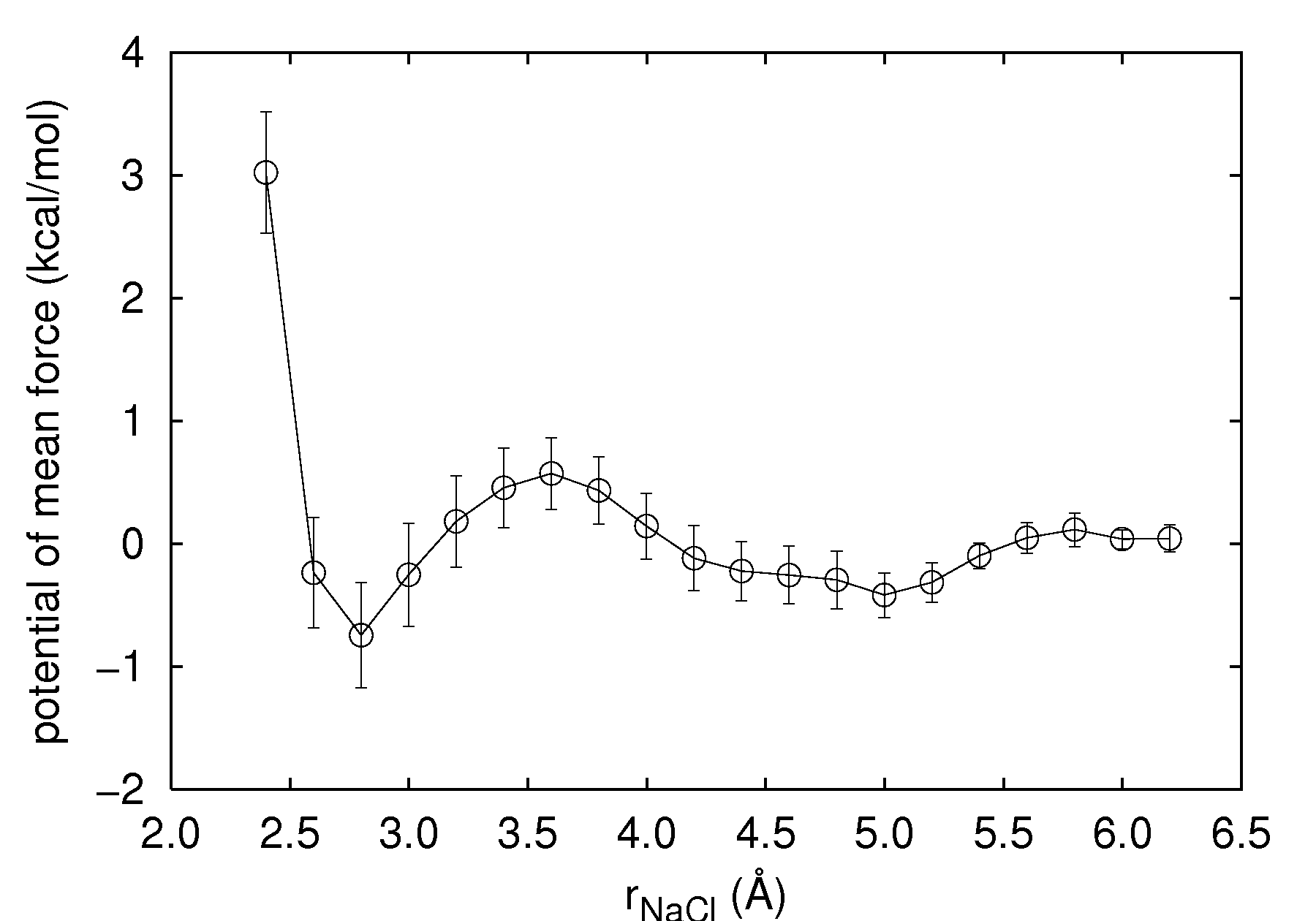
図3.アルカリ―ハライドの原子間距離と自由エネルギーの関係
まず、結晶の最近接原子間距離に相当する位置(rNaCl=2.8 Å程度)に準安定状態が存在しますが、これはCIPが得られていることを反映しています。また、CIPからアルカリハライドを引き離すには障壁エネルギーが存在することが分かります。さらに、 5 Å程度の位置に次の準安定状態がありますが、これはSSIPが得られていることを反映しています。
図3より、予想されたようにCIPとSSIPの間には、障壁エネルギーが存在することが確認できます。その大きさは、本計算の範囲では、CIPから見ると1.6 kcal/mol程度、SSIPから見ると0.9 kcal/mol程度です。
CIP, SSIP構造の原子配置#
図4に、Na-Cl間距離が2.8 Åの場合と4.8 Åの場合の原子配置を示します。
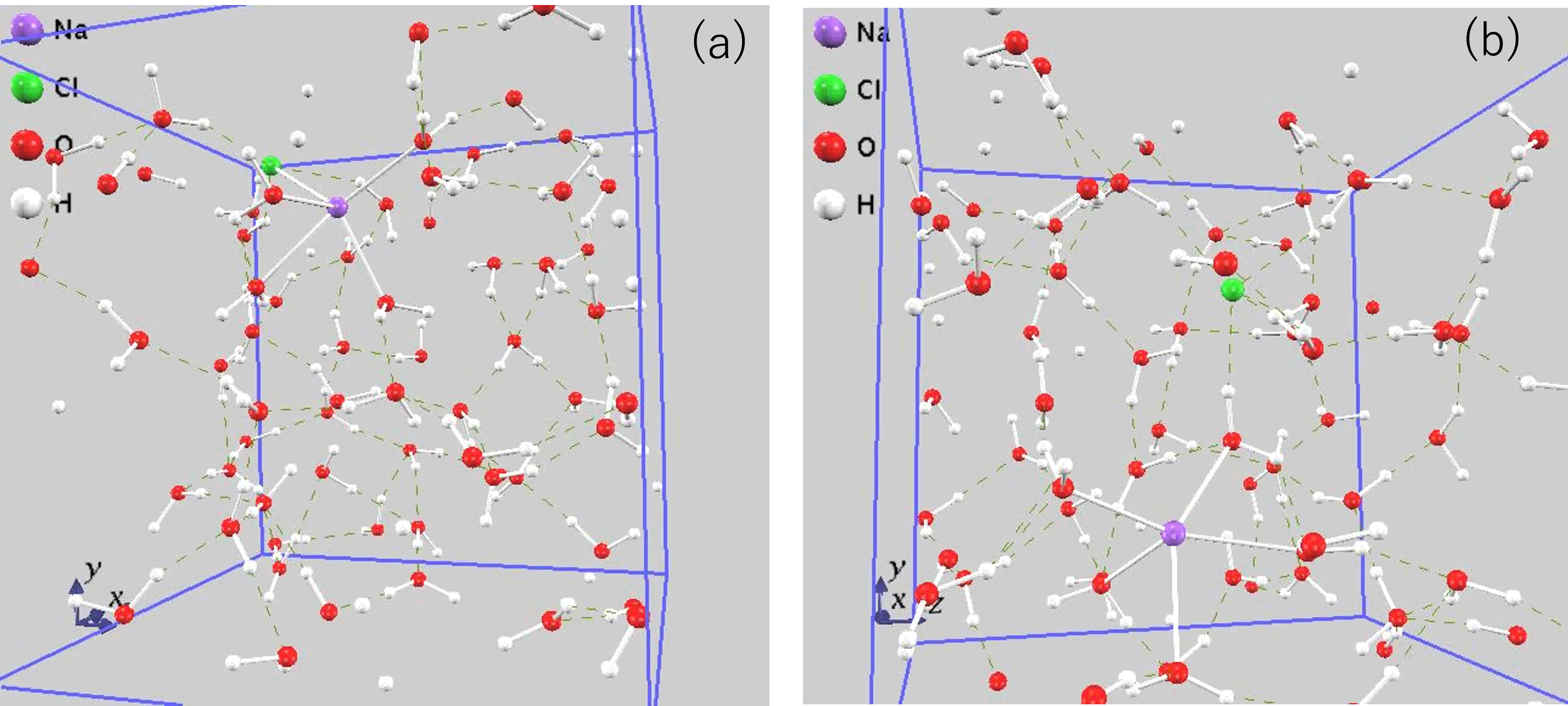
図4.原子配置のスナップショット (a) rNaCl=2.8 Åの場合、(b) rNaCl=4.8 Åの場合.図中の破線は水素結合を表します。
図4(a)の原子配置を見ると、ナトリウム原子と塩素原子が隣接しており、またナトリウムの周りには水分子の酸素原子が、塩素原子の周りには水分子の水素原子が存在している様子がわかります。このような構造が、まさにCIPの原子配置として考えられているものです。他方図4(b)を見ると、Na,Clはそれぞれ水分子に囲まれているのですが、その内の1つの水分子は酸素がナトリウムに結合し、また水素が塩素に水素結合した状態となっています。この、ナトリウム-水分子-塩素という複合体が、まさにSSIPの構造です。図4(a)および(b)より、確かにCIP,SSIPという構造が実現することを確認することができました。
まとめ#
Blue moon法を用いた2つの計算事例を紹介しました。まず、H2O2分子の回転障壁計算では、得られた自由エネルギープロファイルが拘束条件付き構造最適化の結果とよく一致し、手法の妥当性が確認されました。次に、水中における塩化ナトリウム(NaCl)の解離過程を解析し、イオンが隣接する接触イオンペア(CIP)と水分子を挟む溶媒分離イオンペア(SSIP)という2つの準安定状態の存在と、両者の間のエネルギー障壁(約1.6 kcal/mol)を定量的に明らかにしました。さらに、シミュレーションのスナップショットからCIPとSSIPに特徴的な原子構造が実現していることも確認できました。これらの事例は、Blue Moon法が分子の内部回転から化学結合の解離に至るまで、様々な現象の自由エネルギー変化を解析するための有効な手法であることを示しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- M. Sprik and G. Ciccotti, J. Chem. Phys. 109, 7737 (1998).
- A. Pohorille, C. Jarzynski, C. Chipot, J. Phys. Chem. B 114, 10235 (2010).
- T. Lelievre, M. Rousset, G. Stoltz, Free-Energy Computations: A Mathematical Perspective, Imperial College Press, 2010.
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学