タングステン(100)表面におけるジグザグ再構成構造の第一原理計算#

タングステン(W)は高融点金属として知られ、その表面物性は触媒や電子デバイスの分野で重要です。特にW(100)表面は、高温での1x1構造から、低温で原子がジグザグ状に再配列するc(2x2)再構成構造に相転移することが実験的に観測されています。この表面再構成は、表面の電子状態と密接に関連しており、材料の性能に大きな影響を与えます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、W(100)面の1x1表面とc(2x2)ジグザグ再構成構造のどちらがエネルギー的に安定であるかを評価し、その駆動力について電子状態の観点から解明します。
Keywords: 第一原理計算, DFTシミュレーション, 表面エネルギー, 表面再構成, ジグザグ(zigzag)構造, タングステン, スラブモデル, 線形フィッティング法, 状態密度
計算モデルと計算条件#
本計算は絶対零度における基底状態を評価するものであり、低温での実験条件と整合します。計算モデルとして、W(100) 1x1表面と、2x2表面スーパーセルの2種類のスラブモデルを構築しました。最適化したWバルクの格子定数 3.18 Å を用い、それぞれ7, 9, 11, 13層のモデルを作成しました。真空層の厚さは 15 Å にしています。2x2表面スーパーセルの初期構造では、原子を対称な位置からわずかにずらして計算を開始しています。
どちらのモデルでも、スラブ中央の3層(図1で明るい色で表示)の原子座標を固定したうえで、その他の原子(暗い色で表示)を自由に動かして構造を最適化しました。
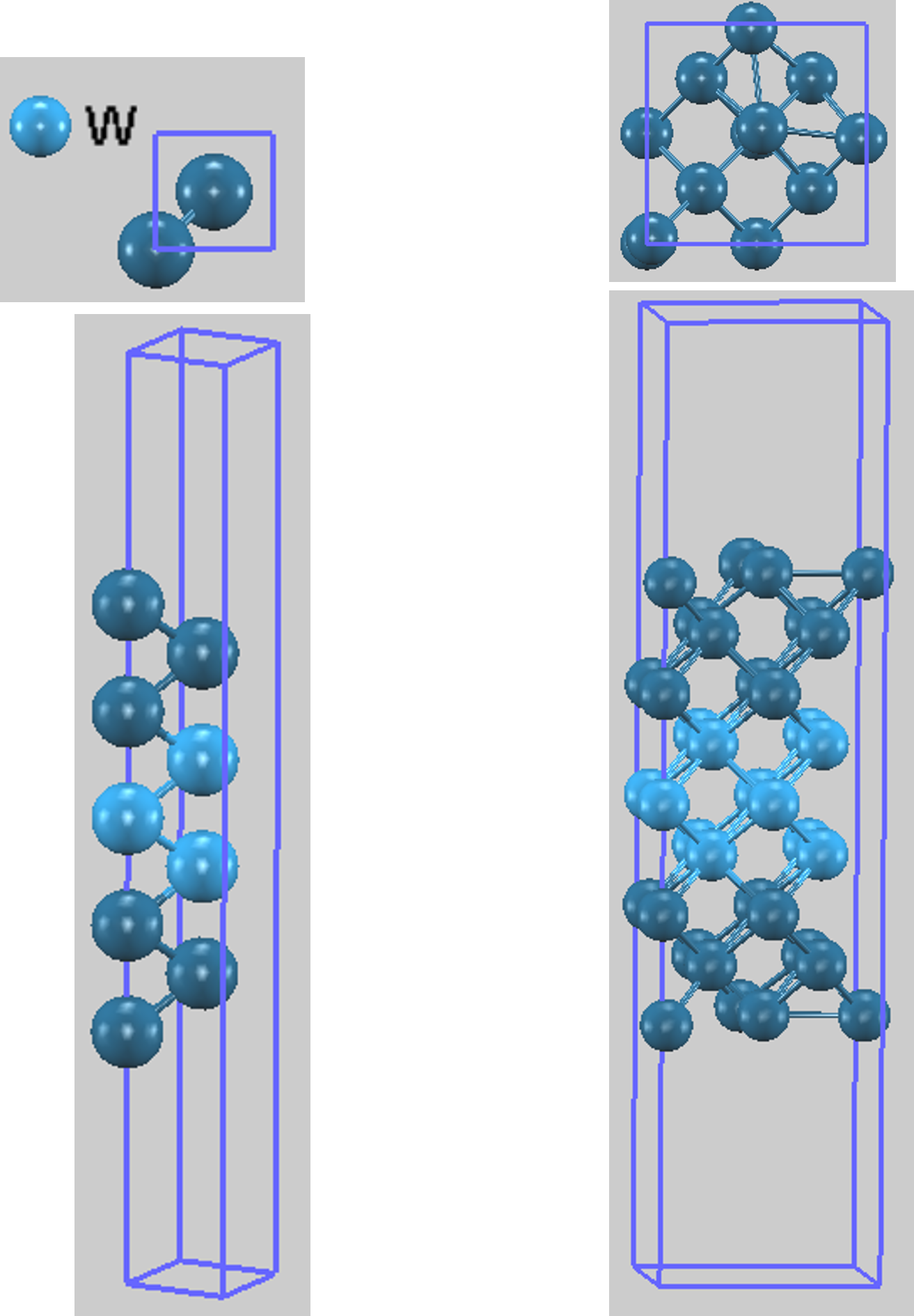
図1. 計算に用いたW(100)表面のスラブモデルの例。(左) 1x1構造、(右) 2x2スーパーセルの初期配置をそれぞれ上面図と側面図で示しています。中央の明るい色の3層が固定原子層です。
本解析で用いた主な計算条件は表1に示されています。
表1. 計算条件の概要
| 項目 | 設定 |
|---|---|
| 擬ポテンシャル | ウルトラソフト擬ポテンシャル |
| 交換相関汎関数 | GGA (PBE) |
| 波動関数のカットオフエネルギー | 25 Rydberg (約340 eV) |
| k点サンプリング (SCF計算) | 1x1 構造: 10x10x1 2x2スーパーセル: 5x5x1 |
計算結果と考察#
表面構造の最適化と表面エネルギーの算出#
構造最適化の結果、2x2スーパーセルモデルでは表面原子が面内で変位し、特徴的なジグザグ構造を形成しました。原子の変位量は約0.27 Åです。図2は、4x4スーパーセルで構造最適化の結果を示します。再構成構造は、ウッドの記法 [1] を用いて2通りの方法で表現できます。
- c(2x2)構造: 下地の(1x1)格子に平行な向きに、縦横2倍の大きさの単位セル(慣習格子)を考えます(図2左)。この大きなセルの四隅と中心 (center) が、構造的に等価な位置となる対称性を持つため、「c(2x2)構造」と呼ばれます。再構成によって生じた原子の変位パターンが、このセルの四隅と中心に繰り返し現れると解釈できます。下地との方位関係が直感的に分かりやすい利点があります。
- 構造: 図2右の点線赤枠で示した単位セルです。これは、この原子配列を表現できる最小の繰り返し単位(基本格子)です。下地の(1x1)セルの辺の長さに対し√2倍の辺を持ち、45度回転 (Rotated) していることを意味します。この単位格子は、2個の原子を含んでいます。
これら2つの表記は、全く同じ原子のジグザグ配列を指しており、c(2x2)構造という呼び方が一般的に広く用いられています。
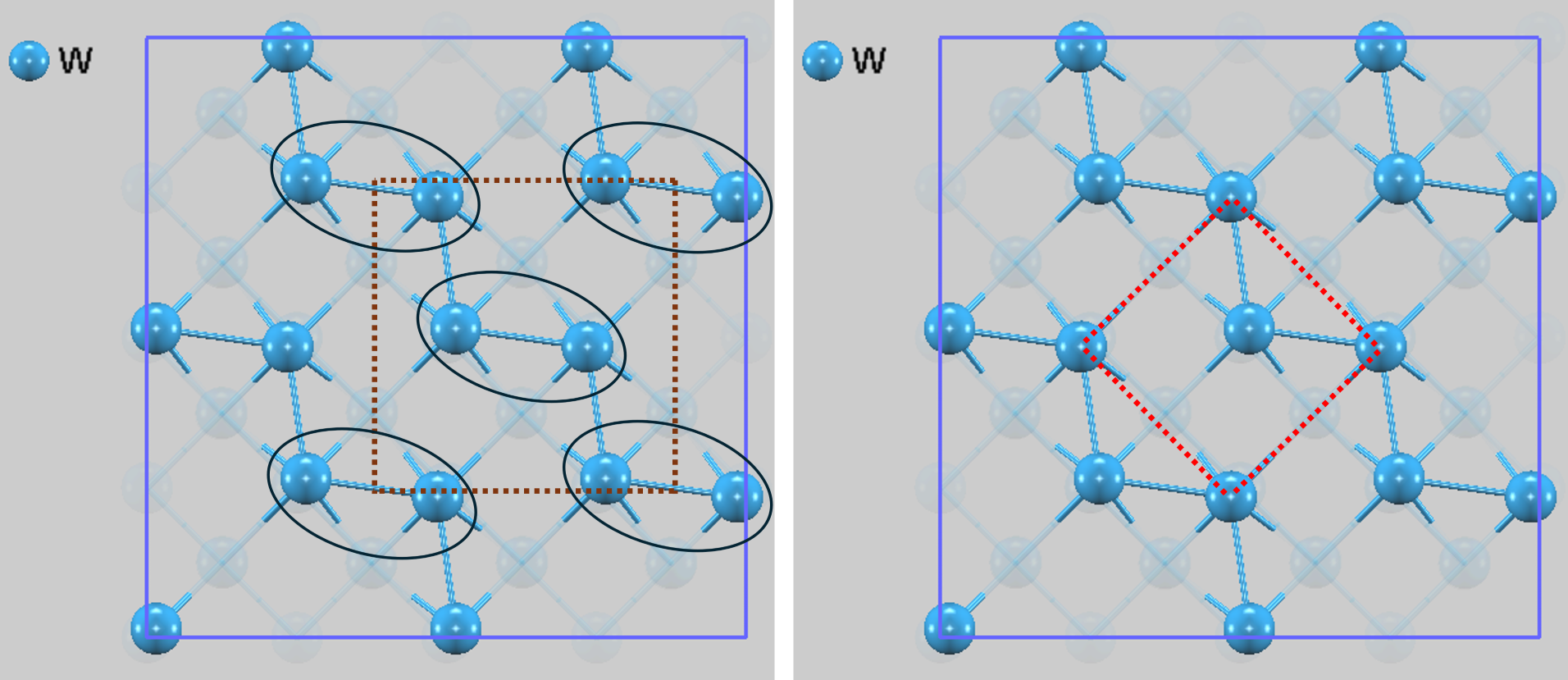
図2. 最適化されたW(100) 2x2スーパーセルの原子配列(上面図、下層の原子は視認性のため半透明で表示)。原子がジグザグに変位し、ペア(黒い楕円)を形成していることが分かります。茶色い点線で示された格子は、下地の(1x1)格子に平行な c(2x2) 慣習格子です。この格子では、原子ペアが四隅と中心に配置されています。一方、赤い点線で示された格子は、この構造の最小単位である 基本格子を示しています。これら二つの表記は、同一の原子配列を異なる視点から記述したものです。
表面エネルギーは、層数()の異なる複数のスラブモデルの全エネルギー()を計算し、その線形関係から高精度に算出する「線形フィッティング法」を用いました。は層数に対して以下の線形関係にあり、この直線の切片から表面エネルギー()を求めます [2]。
図3および図4に示すように、1x1と2x2スーパーセルの両表面で計算データは直線上に非常によく乗り、決定係数(R2)が1.00000000となる精度の高いフィッティングが得られました。
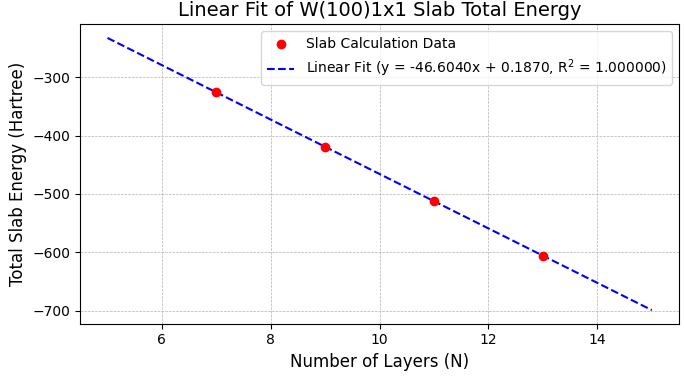
図3. W(100) 1x1表面スラブの全エネルギーと層数の線形関係。
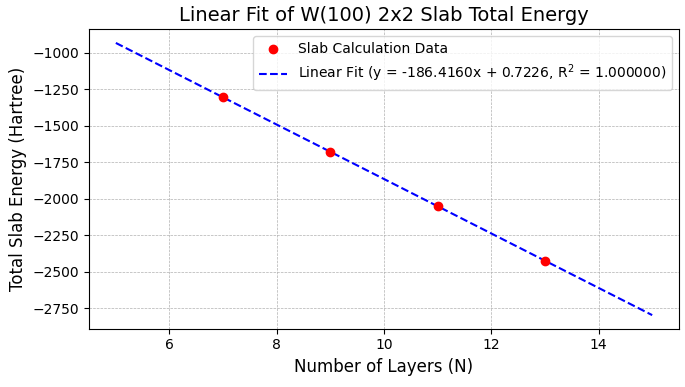
図4. W(100) 2x2スーパーセルの表面スラブの全エネルギーと層数の線形関係。
表面エネルギーの比較と安定性評価#
図3、図4の線形フィッティングの切片 (Hartree単位)とセルの表面積 (Å単位)から換算して得られた各表面のエネルギー(J/m2)を、文献値 と比較して表2にまとめます。
表2. W(100)の表面エネルギー: 本計算と文献値の比較 (単位: J/m2)
| 表面構造 | 本計算値 | 文献値 |
|---|---|---|
| W(100) 1x1 表面 | 4.031 | 4.00 |
| W(100) c(2x2)表面 (zigzag再構成) | 3.894 | 3.90 |
本計算の結果、W(100)面の表面エネルギーは、1x1表面が4.031 J/m2、c(2x2)再構成表面が3.894 J/m2 となりました。c(2x2)再構成表面の方が1x1表面よりも表面エネルギーが約0.14 J/m2低く、より安定であることが定量的に示されました。この結果は、実験で観測される事実 [3] や、先行研究のGGA/PBEによる計算値 [4] とも非常によく一致しており、本解析の妥当性を裏付けています。
電子状態の解析#
表面が再構成することで、なぜエネルギー的に安定化するのでしょうか。その手がかりは電子状態に見ることができます。図5は、W(100) 1x1表面とc(2x2)再構成表面における最表面原子の局所状態密度(LDOS)を比較したものです。
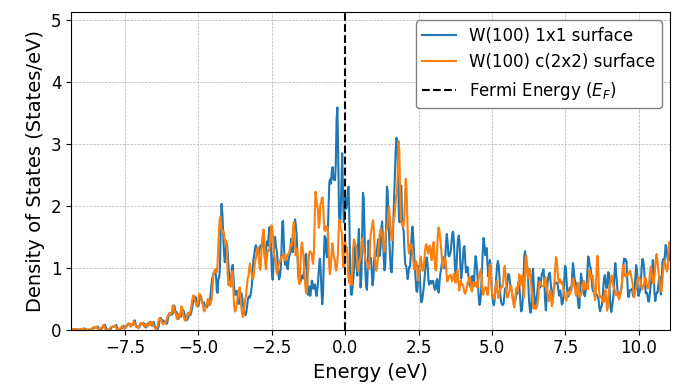
図5. W(100) 1x1表面とc(2x2)再構成表面における最表面原子の局所状態密度(LDOS)の比較。
この図から、c(2x2)再構成表面では、フェルミエネルギー(, 0 eV)付近の状態密度が大きく減少していることがわかります。これは、原子が再配列して新たな結合を形成した結果、電子が占有できるエネルギー準位がフェルミ準位から遠ざかり、電子系の全エネルギーが低下したことを意味します。この種の安定化機構は表面再構成の駆動力となる重要なメカニズムの一つです。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、W(100)表面の1x1構造とc(2x2)ジグザグ再構成構造の安定性を比較しました。高精度な線形フィッティング法を用いて表面エネルギーを算出した結果、c(2x2)再構成構造(3.894 J/m2)は1x1表面(4.031 J/m2)よりもエネルギー的に安定であることが明らかになりました。また、この安定化がフェルミ準位近傍の電子状態密度の減少によってもたらされていることを示しました。これらの結果は、実験や他の理論研究とも整合的であり、第一原理計算が複雑な表面現象のメカニズムを原子・電子レベルで解明するための強力なツールであることを示しています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- E. A. Wood, "Vocabulary of surface crystallography", J. Appl. Phys. 35, 1306 (1964).
- V. Fiorentini and M. Methfessel, "Extracting convergent surface energies from slab calculations", J. Phys.: Condens. Matter 8, 6525 (1996).
- H. Landskron, N. Bickel, K. Heinz, G. Schmidtlein and K. Muller, "LEED intensity analysis of the clean W(100) c(2×2) surface reconstruction", J. Phys.: Condens. Matter 1, 1 (1989).
- Z. A. Piazza, M. Ajmalghan, Y. Ferro, and R. D. Kolasinski, "Saturation of tungsten surfaces with hydrogen: A density functional theory study complemented by low energy ion scattering and direct recoil spectroscopy data", Acta Materialia 145, 388 (2018).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学