Au(110)の表面再構成：欠損原子列構造の安定性評価#

PHASE logo

固体材料の表面は、内部とは異なる原子配列をとる「表面再構成」という現象を示すことがあります。これは、表面エネルギーを最小化するために原子が自発的に再配置するもので、触媒活性や薄膜成長など、表面が関わる多くの物性に影響を与えます。金(Au)の(110)面では、最表面の原子列が一つおきに失われる「1x2 欠損原子列（Missing Row）構造」が形成されることが実験的に知られています。本解析では、第一原理計算ソフトウェアAdvance/PHASE を用い、このAu(110)面の理想表面(1x1)と欠損原子列構造(1x2)の表面エネルギーを計算し、どちらの構造がより安定であるかを定量的に評価します。

Keywords: 第一原理計算, 表面エネルギー, 表面再構成, 欠損原子列構造, 金, スラブモデル, 線形フィッティング法

計算方法：表面エネルギーの算出#

表面エネルギー( $\gamma$ )を計算する手法として、スラブモデルの全エネルギー( $E_{\text{slab}}$ )、バルク（内部）の原子あたりのエネルギー( $E_{\text{bulk}}$ )、表面積( $A$ )を用いる方法が基本となります。

$\gamma = \dfrac{E_{\text{slab}} - N \cdot E_{\text{bulk}}}{2A}$

ここで、 $N$ はスラブモデルに含まれる原子数です。しかし、この手法では $E_{\text{slab}}$ と $E_{\text{bulk}}$ の計算条件のわずかな不整合により、スラブの層数を増やしても $\gamma$ の計算値が収束しにくい問題があります。

そこで本解析では、より高精度な「線形フィッティング法」を採用しました。この手法は、層数または原子数 $N$ に対してスラブの全エネルギーが線形に変化することを利用します [1]。

$E_{\text{slab}}(N) \approx 2\gamma A + N \cdot E_{\text{bulk}}^{\text{fit}}$

この式の切片 ( $2\gamma A$ ) から表面エネルギー $\gamma$ を、傾き ( $E_{\text{bulk}}^{\text{fit}}$ ) からスラブ内部の原子1個あたりのエネルギーを、それぞれ高精度に求めることができます。

計算モデルと計算条件#

計算モデルとして、理想的なAu(110) 1x1表面と、再構成した1x2欠損原子列構造の2種類のスラブモデルを構築しました。最適化したAuバルクの格子定数 4.173 Å を使用しています。

Au(110) 1x1モデル（理想表面）: 鏡映対称性を持つ9, 11, 13, 15層のモデルを作成しました。
Au(110) 1x2モデル（欠損原子列構造）: スラブの上下の最表面からそれぞれ原子列を一つずつ取り除いたモデルです。10, 12, 14, 16層のモデルを作成しました。

どちらのモデルでも、真空層を十分に確保し、スラブ中央の1層（理想表面の場合）もしくは2層（欠損原子列構造の場合）の原子座標を固定したうえで、その他の原子（図1で暗い色で表示）を自由に動かして構造を最適化しました。

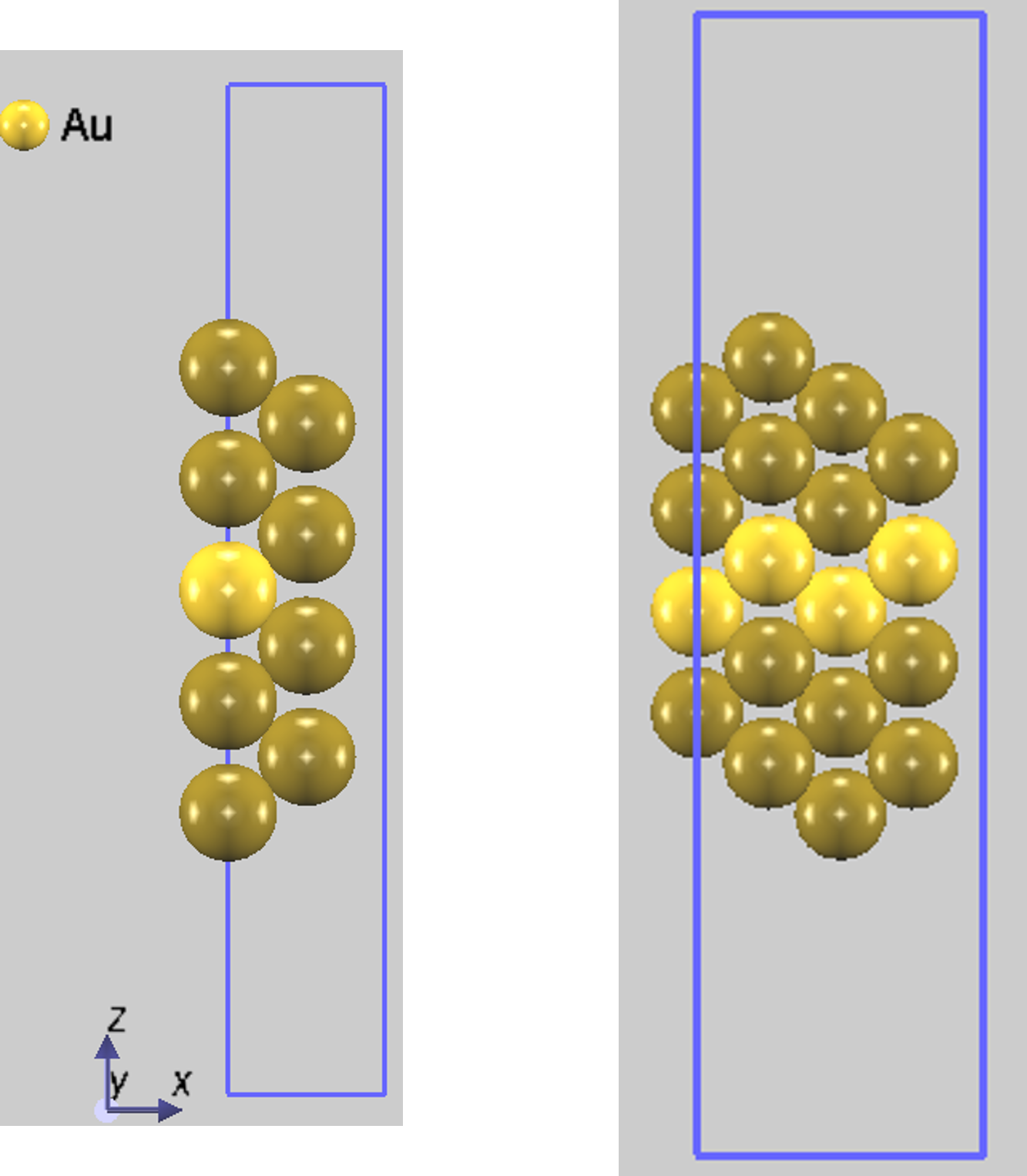
Au(110) 1x1モデルと1x2モデル

図1.　(左) Au(110) 1x1理想表面、(右) Au(110) 1x2欠損原子列構造の初期構造モデルの例。中央の明るい色の原子層が固定され、暗い色の原子が構造最適化で緩和されます。

本解析で用いた主な計算条件は表1に示されています。

表1.　計算条件の概要

項目	設定
擬ポテンシャル	ウルトラソフト擬ポテンシャル
交換相関汎関数	GGA (PBE)
波動関数のカットオフエネルギー	25 Rydberg (約340 eV)
k点サンプリング	1x1理想表面: 11x8x1 1x2欠損原子列構造: 11x4x1

計算結果と考察#

構造最適化と線形フィッティング#

構造最適化の結果、どちらのモデルでも表面層が内側に向かって緩和（収縮）する様子が確認されました。これは、表面の原子がバルク（内部）の原子に比べて隣接する原子の数が少ない（配位数が低い）ためです。結合相手を失った表面原子は、残された内側の原子とより強い結合を形成しようとして原子間距離を縮め、より安定な状態になろうとします。この現象は一般的に「表面緩和」として知られています。

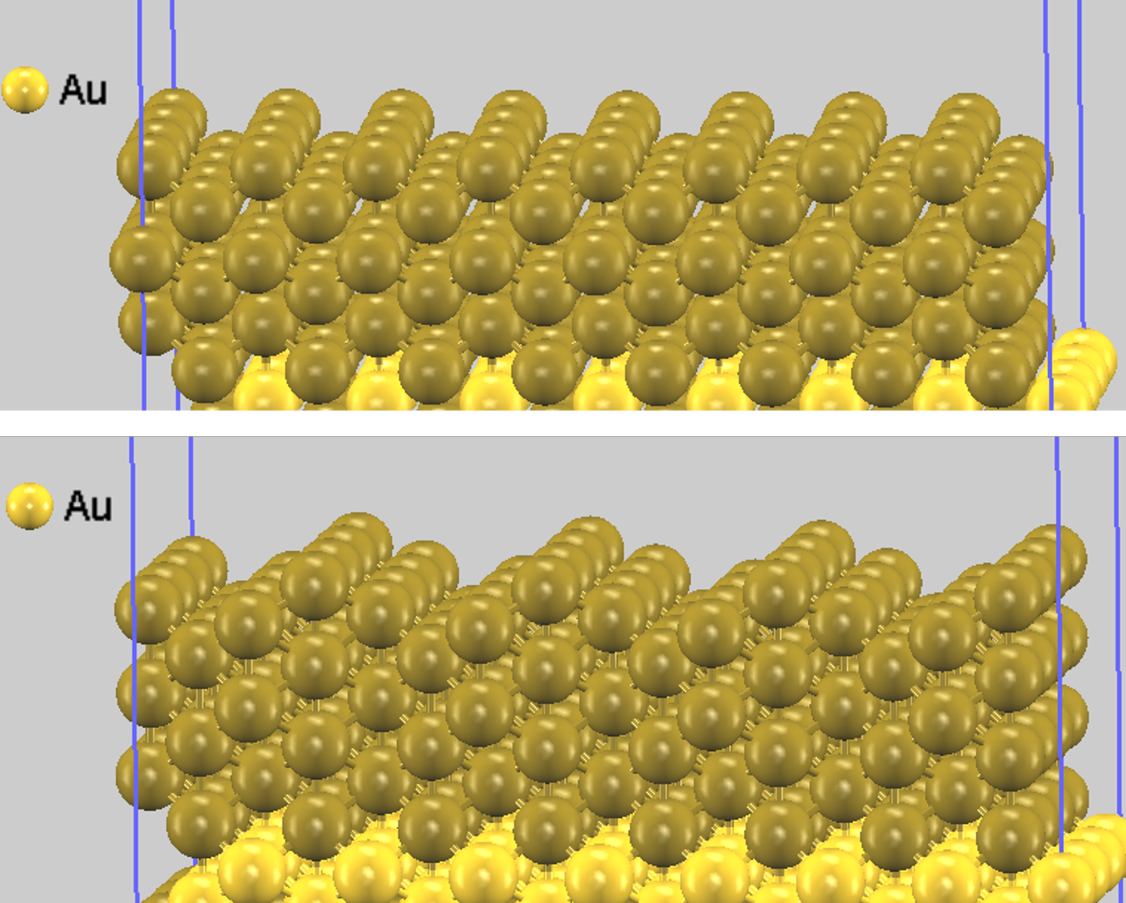
Au(110) 1x2モデルの構造最適化結果

図2.　(上) Au(110) 理想表面、(下) Au(110) 欠損原子列構造の最適化後の安定構造（明るい色の原子が固定され、暗い色の原子が緩和されます）。視覚的に分かりやすくためスーパーセルで示しています。欠損原子列構造の表面に凹凸が形成され、原子が内部に沈み込むように緩和している様子がわかります。

次に、層数（原子数）の異なる各スラブモデルの全エネルギーをプロットし、線形フィッティングを行いました。図3および図4に示すように、1x1理想表面、1x2欠損原子列構造の両方で、計算データは直線上に非常によく乗り、決定係数（R²）が1.000000となる精度の高いフィッティングが得られました。これは、本計算手法の信頼性が高いことを示しています。

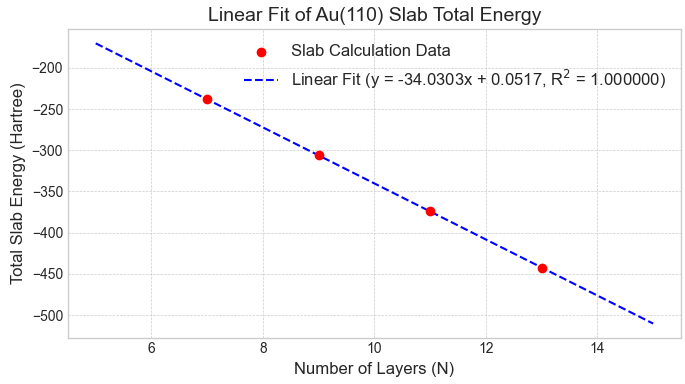
Au(110) 1x1の線形フィッティング

図3.　Au(110) 1x1理想表面スラブの全エネルギーと層数の線形関係。

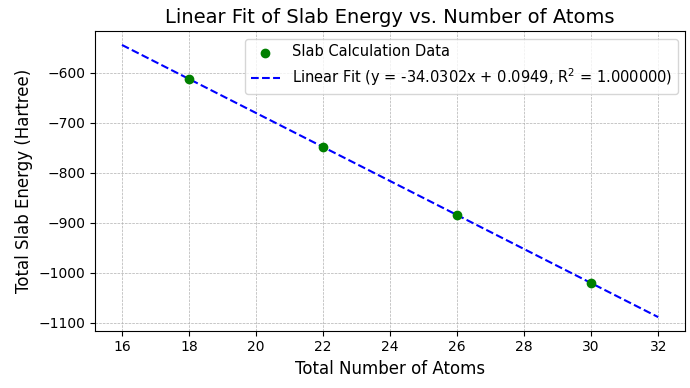
Au(110) 1x2の線形フィッティング

図4.　Au(110) 1x2欠損原子列構造スラブの全エネルギーと原子数の線形関係。

【補足】 1x2欠損原子列構造の場合、最表面の原子数が内部の層の原子数と異なるため、層数と全原子数は単純な比例関係にありません。この場合、横軸を層数としてフィッティングすることも可能ですが、切片にバルクエネルギーの成分が含まれるため更なる処理が必要となります。そこで、図4のように横軸を全原子数とすることで、より直接的かつ物理的に明快な形でフィッティングを行うことができます。

表面エネルギーの比較と考察#

線形フィッティング法によって得られた各表面のエネルギーを、同じ計算手法(GGA/PBE)を用いた文献値 [2]と比較して表2にまとめます。計算で用いられる原子単位系のエネルギー（Hartree）と表面積（Å²）から、最終的にSI単位系（J/m²）へ換算しています。

表2.　Au(110)表面の表面エネルギー: 本計算と文献値の比較 (単位: J/m²)

表面構造	本計算値 (GGA/PBE)	文献値 [2] (GGA/PBE)
Au(110) 1x1 (理想表面)	0.915	0.91
Au(110) 1x2 (欠損原子列構造)	0.840	0.83

本計算の結果、Au(110)面の表面エネルギーは、1x1理想表面が0.915 J/m²、1x2欠損原子列構造が0.840 J/m² となりました。欠損原子列構造の方が理想表面よりも表面エネルギーが低く、より安定であることが定量的に示されました。この結果は、実験で観測される事実 [3] や、先行研究の計算値とも非常によく一致しており、本解析の妥当性を裏付けています。

では、なぜ原子列がなくなる方がエネルギー的に安定なのでしょうか。これは、最表面の原子列が一つなくなることで、残された原子が再配置し、より安定な局所構造を形成できるためです。具体的には、露出した原子が(111)面に似た、より密で安定な微小な面（マイクロファセット）を形成するように緩和します。Auのような面心立方格子金属では(111)面が最も安定な面であるため、この再構成によって表面全体のエネルギーが低下するのです。

このエネルギー差が、Au(110)表面で自発的に原子列が欠損し、1x2再構成構造が形成される駆動力となっています。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、Au(110)表面の1x1理想構造と1x2欠損原子列再構成構造の安定性を比較しました。高精度な線形フィッティング法により表面エネルギーを算出した結果、欠損原子列構造（0.840 J/m²）は理想表面（0.915 J/m²）よりもエネルギー的に安定であることが明らかになりました。この結果は、実験や他の理論研究とも整合的であり、第一原理計算が複雑な表面現象のメカニズムを原子レベルで解明するための強力なツールであることを示しています。

参考文献#

V. Fiorentini and M. Methfessel, "Extracting convergent surface energies from slab calculations", J. Phys.: Condens. Matter 8, 6525 (1996).
R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson, and S. P. Ong, "Surface energies of elemental crystals", Sci. Data 3, 160080 (2016).
E. Vlieg, I. K. Robinson, and K. Kern, "Relaxations in the missing-row structure of the (1×2) reconstructed surfaces of Au(110) and Pt(110)", Surf. Sci. 233, 248 (1990).