コンテンツにスキップ

第一原理計算による原子電荷の評価：共有結合・イオン性物質から高分子まで#

PHASE logo

固体や分子の物性を理解する上で、構成原子がどの程度帯電しているかを示す「原子あたりの電荷量」は、非常に重要な指標となります。例えば、触媒の活性サイトの特定、電池材料におけるイオンの挙動解析、分子間相互作用の解明など、多岐にわたる分野で物理・化学的な洞察を与えてくれます。本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装された複数の電子密度分割法、および外部プログラムと連携するBader電荷解析法を紹介し、その有効性と適切な手法選択の重要性について検証します。

Keywords: 第一原理計算, 原子電荷, 電子密度分割, Bader電荷解析, 共有結合, イオン結合, 高分子, Becke-Fuzzy分割, 多面体分割

計算手法：電子密度をどう分割するか？#

原子電荷は、計算された電子密度を、いかにして各原子に「公平に」分配するかによって定義されます。ここでは、Advance/PHASEに実装されている手法と、外部プログラムと連携するBader電荷解析法を紹介します。

Advance/PHASEに実装された手法#

  • 球面分割法: 各原子中心に設定した球の内部の電子をその原子に帰属させます。

  • 多面体分割法: 各原子の周囲に、図1のように隣接原子との間に設けた垂直二等分面によって構成される多面体を作成し、その内部の電子密度を中心原子の電荷として割り当てます。 電子が局在している金属やイオン性結晶に特に有効です。

  • Becke-Fuzzy分割法: 空間を明確な境界で区切るのではなく、連続的で滑らかな「重み関数」を用いて電子密度を分割します [1]。 これにより、電子密度が図2の「原子iおよびjの電子密度」のように滑らかに分割され、異なる原子に属する電子密度の重なりが許容されます。 このため、原子軌道の重なりが大きい共有結合を含む系に適しているとされます。

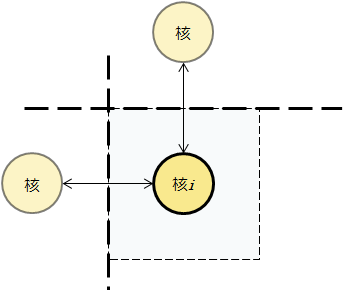
原子iの核を囲む多面体

図1. 原子iの核を囲む多面体
(多面体分割法)

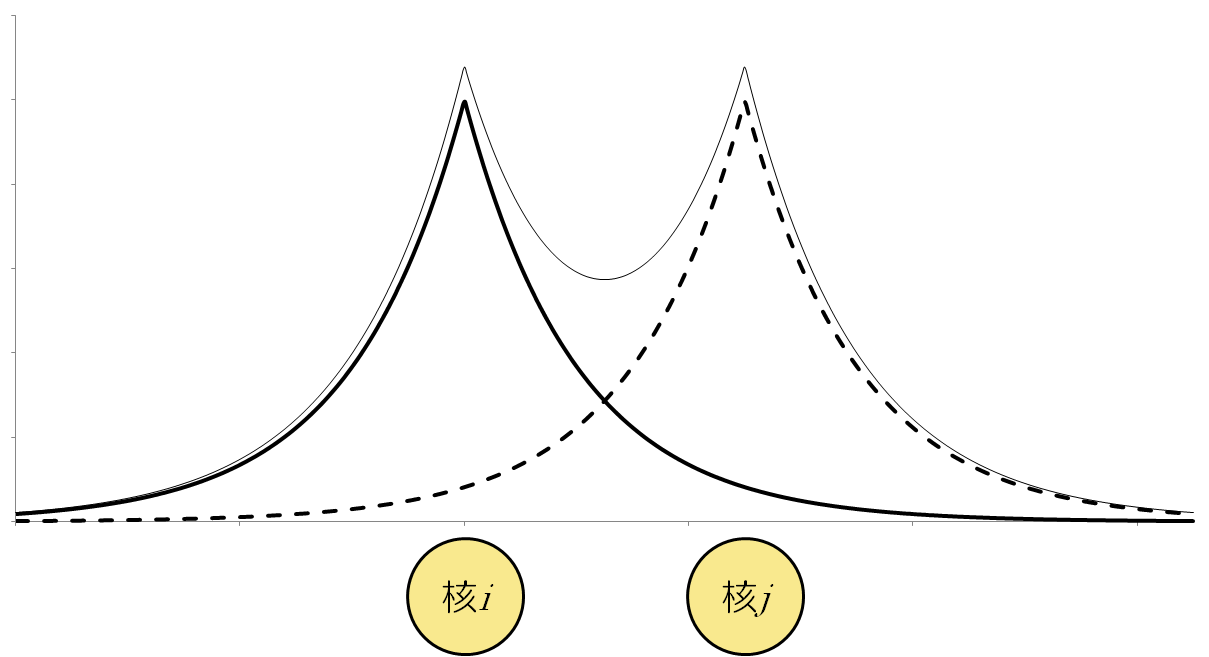
原子iおよびjの電子密度

図2. 原子iおよびjの電子密度
(Becke-Fuzzy分割法)

Bader電荷解析法：外部プログラムとの連携#

Bader電荷解析は、電子密度の勾配がゼロになる曲面（ゼロフラックス面）で空間を分割し、各領域（Bader体積）内の電子をその原子に帰属させる、広く知られた手法です [2]。Advance/PHASEでは、外部のBaderプログラム [3] と連携することで、この解析を手軽に実行できます。

  1. PAW法を有効にし、全電子密度および価電子密度をcube形式で出力する設定で、SCF計算を実行します。

  2. 計算後、結果解析GUIからBader charge analysis機能を利用します。これにより、外部プログラムbaderが呼び出され、解析結果がファイルに出力されます。

  3. 出力されたCHARGE（原子に帰属する電子数）と、計算に使用した擬ポテンシャルで定義されている価電子数から、最終的な原子電荷を算出します。
    原子電荷 = 価電子数 - CHARGE計算値

このBader電荷解析法は、他の分割法と同様に、系の性質を評価するための有力な選択肢の一つです。

計算結果と考察#

共有結合性分子#

まず、共有結合性の強い分子群について、Advance/PHASEに実装された手法で計算した原子電荷の結果を表1に示します。交換相関汎関数にはGGA-PBEを使用しました。比較として、Gauss関数基底の計算も行いました。具体的には、Gaussian09 [4] プログラムを用い、DFT計算（B3LYP/6-311G**）により基底状態電子密度を決定し、CHelpG法[5]で原子あたりの電荷量を算出しました。

表1. 共有結合性分子における原子あたりの電荷量 (e)

分子 原子 Advance/PHASE Gaussian09
球面 多面体 Becke-Fuzzy
CH4 C -0.536 1.810 -0.576 -0.360
H 0.595 -0.456 0.144 0.090
C6H6 C -0.617 0.479 -0.190 -0.079
H 0.590 -0.479 0.191 0.080
H2O H 0.563 -0.378 0.198 0.371
O 0.307 0.751 -0.392 -0.742
HCl H 0.660 -0.639 0.380 0.253
Cl -0.101 0.639 -0.374 -0.253

表1の結果から、共有結合性分子の計算にはBecke-Fuzzy分割法が最も適していることがわかります。Gaussian09(CHelpG法)の結果と絶対値は異なるものの、電荷の符号や傾向をよく再現しており、定量的な評価も可能であると言えます。

イオン性物質#

次に、イオン結合性の強いNaClおよびLiClについて計算した結果を表2に示します。

表2. イオン性物質における原子あたりの電荷量 (e)

系 原子 Advance/PHASE Gaussian09
多面体 Becke-Fuzzy
NaCl (分子) Na 0.639 -0.231 0.782
Cl -0.639 0.261 -0.782
LiCl (分子) Li 0.462 -0.247 0.749
Cl -0.462 0.263 -0.749
NaCl (結晶) Na 0.356 -1.477 -
Cl -0.356 1.411 -

イオン結合が支配的な化合物では、多面体分割法が有効であることが示されました。電子が各原子の近傍に強く局在しているため、原子間で空間を明確に区切るこの手法が良い近似となります。

大規模系への応用：高分子の例#

大規模系の計算例として、図3に示す有機高分子であるポリエチレンテレフタレート（PET）の4量体モデルにBecke-Fuzzy分割法を適用し、その有効性を検証しました。

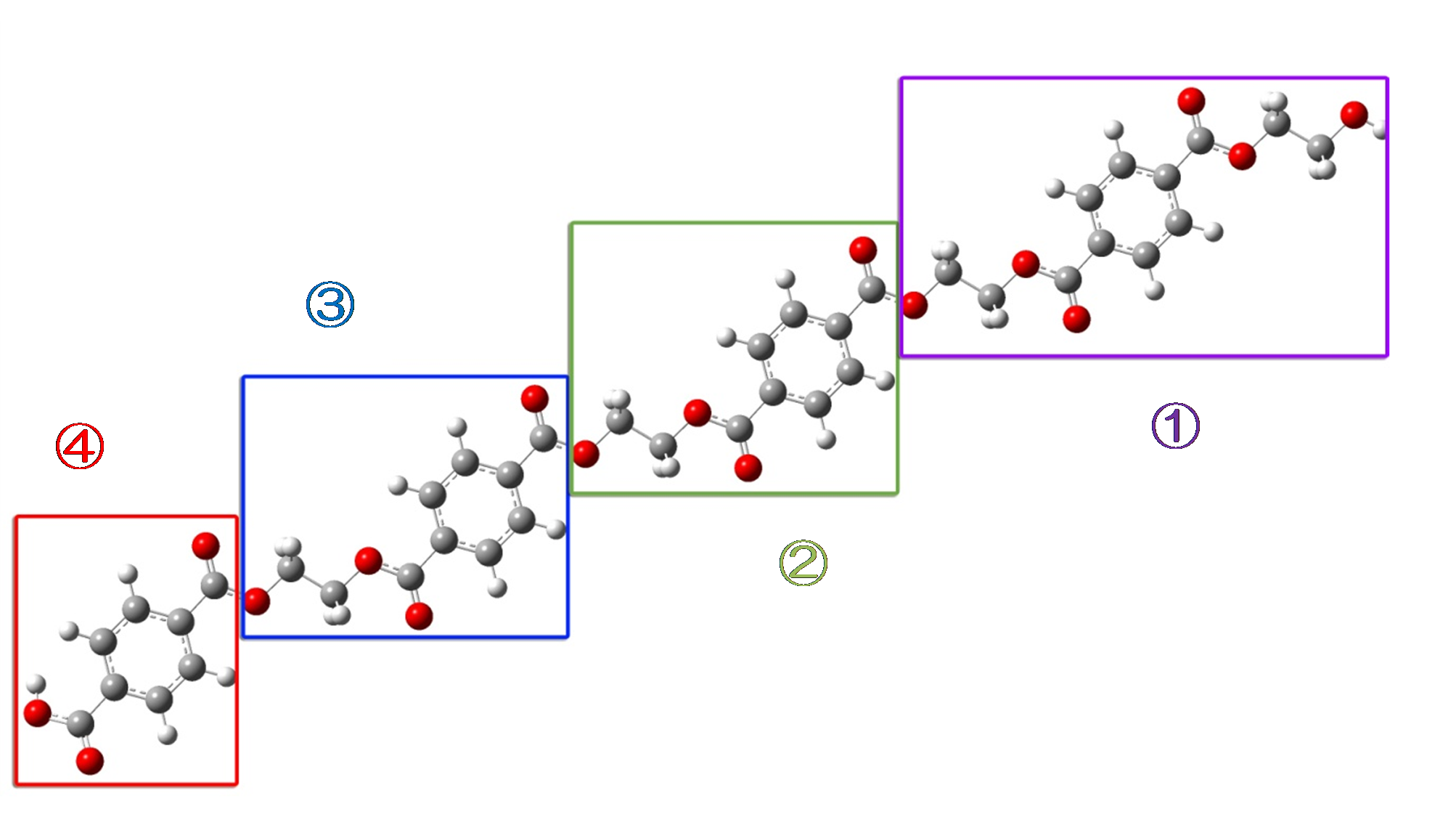
ポリエチレンテレフタレート(PET)4量体の分子構造

図3.　ポリエチレンテレフタレート(PET)4量体の分子構造モデル。赤い球は酸素、灰色の球は炭素、白い球は水素原子を示す。①～④は誤差評価を行ったフラグメントを表します。

Advance/PHASE (Becke-Fuzzy法) と Gaussian09 (CHelpG法) で計算した電荷の差を、フラグメント毎の絶対誤差平均として評価しました。

表3. PETの各フラグメントにおける電荷の絶対誤差平均

フラグメント 電荷の絶対誤差平均
① 0.254
② 0.297
③ 0.300
④ 0.321

比較対象としたGaussian09での計算値自体も、計算設定によって0.2～0.3程度は変動することが知られています。これを踏まえると、今回Advance/PHASEで得られた誤差は許容範囲内であり、Becke-Fuzzy分割法は大規模系に対してもGauss関数基底の計算結果を十分良く再現していると言えます。

Bader電荷解析の適用例#

Bader電荷解析法を、共有結合性のSi（シリコン）結晶と、イオン結合性のTiO2（酸化チタン）に適用した例を示します。

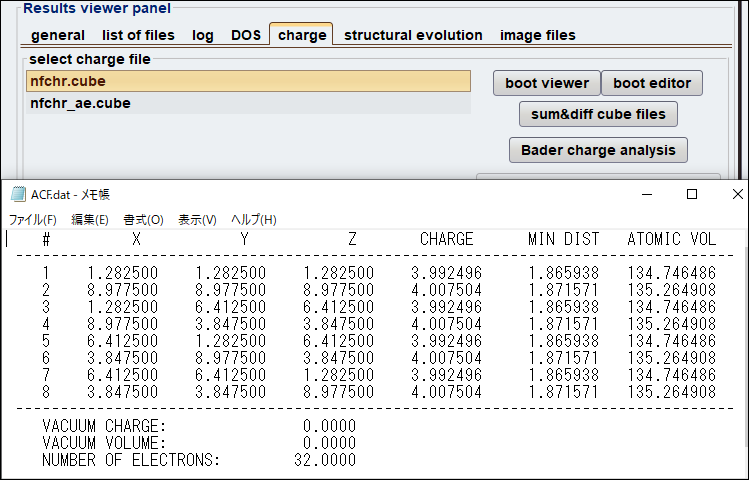
Si8のBader電荷解析

図4.　Si（セル内原子8個）に対するBader電荷解析。

  • Si結晶: 計算に使用した擬ポテンシャルではSiの価電子数は4と定義されています。図4に示すように、Bader解析の結果、各Si原子に帰属する電子数（CHARGE）は約4.0でした。したがって、原子電荷は 4 - 4.0 = 0.0 となり、電荷が中性であることが正しく示されました。

  • TiO2結晶: Ti原子の価電子数は12と定義されています。Bader解析によると、Ti原子に帰属する電子数は9.79でした。よって、Tiイオンの電荷は 12 - 9.79 = +2.21 と計算されます。この+2.2という値は、文献での計算結果 [6, 7] ともよく一致しており、Bader電荷解析法との連携の有効性を示しています。

まとめ#

本解析により、第一原理計算における原子電荷の評価には複数の有効なアプローチがあることが示されました。普遍的に万能な電荷計算法はなく、計算対象の化学的性質に応じて、適切な手法を選択することが重要であることが明らかになりました。

  • ✅共有結合性の強い系（有機分子、高分子など）には、原子間の電子の重なりを滑らかに表現できるBecke-Fuzzy分割法が適しています。

  • ✅イオン結合性の強い系（イオン結晶など）には、電子の局在性を反映しやすい多面体分割法や、物理的描像の明確なBader電荷解析法が有効です。

このように、適切な手法を使い分けることで、平面波基底を用いた第一原理計算からも、信頼性の高い原子電荷情報を引き出すことが可能となります。

参考文献#

  1. A. D. Becke, J. Chem. Phys. 88, 2547 (1988).

  2. G. Henkelman, A. Arnaldsson, and H. Jónsson, Computational Materials Science 36, 354 (2006).

  3. https://theory.cm.utexas.edu/henkelman/research/bader/

  4. Gaussian 09, Revision A.1, M. J. Frisch, et al., Gaussian, Inc., Wallingford CT, 2009.

  5. C. M. Breneman, K. B. Wiberg, J. Comp. Chem. 11, 361 (1990).

  6. X. Li et al., Acta Materialia 57, 5882 (2009).

  7. G. C. Vásquez et al., Scientific reports 8, 8740 (2018).

関連ページ#