第一原理MDを用いたアモルファスシリコンの構造解析#

アモルファス（非晶質）材料は、太陽電池やディスプレイ、相変化メモリなど、現代のエレクトロニクスに欠かせません。しかし、結晶のような周期構造を持たないため、その原子レベルの乱れた構造を実験的に決定することは容易ではありません。そこで、計算科学、特に第一原理計算に基づく分子動力学（MD）シミュレーションが、このようなアモルファス構造を原子レベルで明らかにする強力なツールとなります。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、代表的なアモルファス材料であるシリコン（a-Si）を対象に、溶融急冷法（Melt-Quench Method）によるアモルファス構造の作成と、その構造の妥当性の評価を行います。

Keywords: 第一原理計算, 分子動力学(MD), 溶融急冷法, アモルファスシリコン(a-Si), 動径分布関数(RDF)

計算手法#

アモルファス構造の作成には、計算機上で物質を一度高温で融解させ、その後急速に冷却することで非晶質状態を再現する「溶融急冷法」を用います。本解析では、Advance/PHASEを用いて以下のステップで計算を実行しました。

初期構造の作成: 適切な密度を持つランダムな原子配置を初期構造として準備します。Advance/PHASEに同梱されているPACKMOL [1] およびM3GNet [2] を使用すれば、指定した空間内に原子同士が極端に接近しないように配置できるため、効率的に初期構造を作成できます。
高温での融解 (Melting): 作成した初期構造を、NVTアンサンブル（原子数、体積、温度が一定の条件）のもとで、融点より十分に高い温度（本解析では5000 K）まで昇温し、一定時間（例えば10000 steps）保持します。これにより原子は液体のように振る舞い、初期構造の情報を失います。
急速冷却 (Quenching): 液体状態の系を、同じくNVTアンサンブルのもとで室温（300 K）まで急速に冷却します。この冷却過程のステップ数（例えば40000 steps）は冷却レートにより設定されます。
緩和 (Relaxation): 最後に、300 Kのまま一定時間（例えば10000 steps）MD計算を続け、構造を安定化させます。

Advance/PHASEでは、これらの連続的な温度変化を伴うプロセスをtemperature_control機能で柔軟に設定できます。開始温度、終了温度、計算ステップ数を指定するだけで、複雑な熱処理プロセスを単一の入力ファイルで制御可能です。また、熱浴の制御手法として、従来のNose-Hoover法に加え、より大きな時間ステップでの計算が可能なLangevin法も選択できます。

計算結果と考察#

本解析は、64個のシリコン（Si）原子を含むスーパーセルを計算モデルとして、5000Kで溶融、300Kまで急冷というシミュレーションを行いました。

エネルギープロファイル#

図1に、Nose-Hoover法で時間ステップdt=100 (a.u.)に設定した場合の溶融急冷シミュレーションにおける、系の全エネルギーと運動エネルギーの時間変化（エネルギープロファイル）を示します。

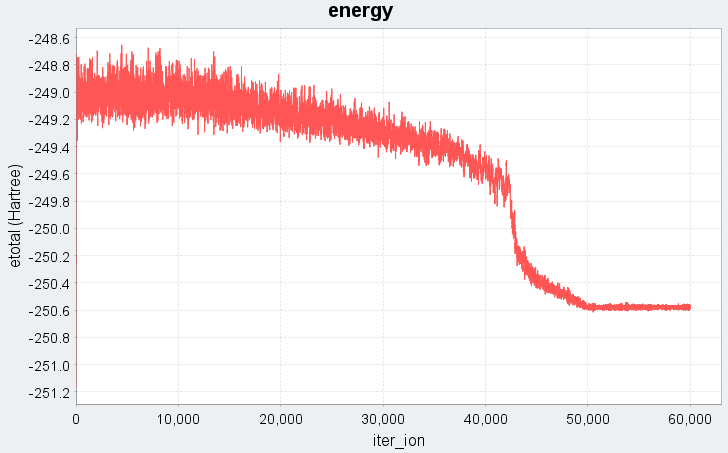
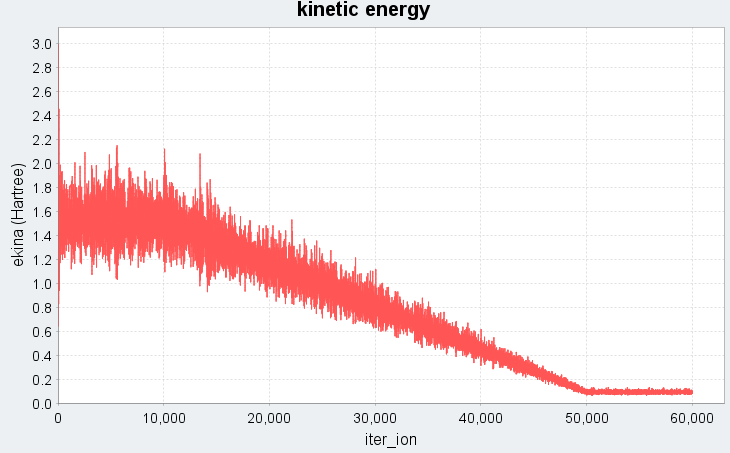図1.　時間ステップdt=100 (a.u.)でのエネルギープロファイル（上：全エネルギー、下：運動エネルギー）。iter_ionはMDステップ数に対応します。

図1では、シミュレーション開始から10000ステップまでは5000 Kの高温状態に対応し、全エネルギー・運動エネルギーともに高い値で推移しています。続く10001ステップから50000ステップの冷却過程では、温度の低下に伴い運動エネルギーが線形的に減少し、それに伴って全エネルギーも急激に下がる様子がわかります。50001ステップ以降は300 Kでの緩和過程であり、エネルギーは低温で安定した状態に落ち着いています。このエネルギープロファイルから、系が液体状態から固体の非晶質状態へと相転移したことが確認できます。

図2では、Langevin法でdt=300 (a.u.)に設定した場合の溶融急冷シミュレーションにおける、系の全エネルギーと運動エネルギーの時間変化（エネルギープロファイル）を示します。シミュレーション開始から3500ステップまでは5000 Kの高温状態に対応し、全エネルギー・運動エネルギーともに高い値で推移しています。続く3501ステップから17500ステップの冷却過程では、温度の低下に伴い運動エネルギーが線形的に減少し、それに伴って全エネルギーも急激に下がる様子がわかります。17501ステップ以降は300 Kでの緩和過程であり、エネルギーは低温で安定した状態に落ち着いています。dt=300ではMDステップ数を大幅に削減できると同時に図1の特徴も再現できており、系が液体状態から固体の非晶質状態へと相転移したことが確認できます。

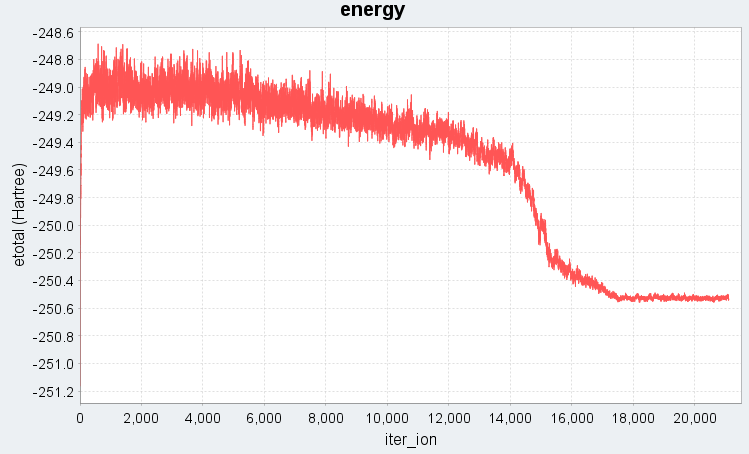
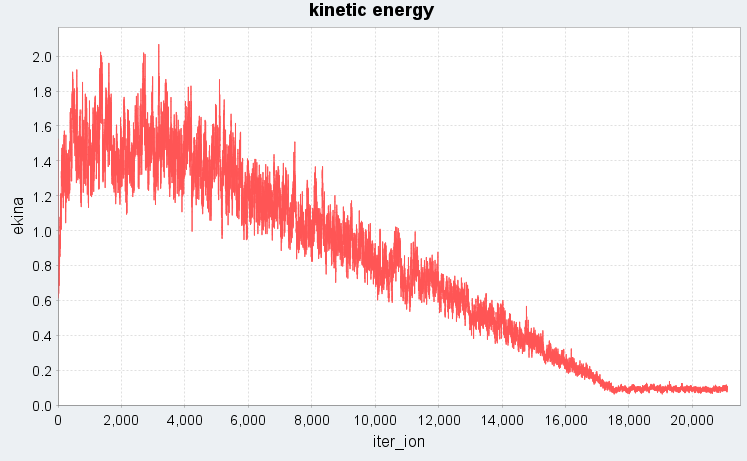
図2.　時間ステップdt=300 (a.u.)でのエネルギープロファイル（上：全エネルギー、下：運動エネルギー）。iter_ionはMDステップ数に対応します。

動径分布関数 (RDF)#

MD (dt=300)で緩和し、さらに構造最適化して得られたアモルファス構造を図3に示します。その妥当性を評価するため、PHASE(GUI)で動径分布関数（Radial Distribution Function, RDF）を計算しました（図4）。

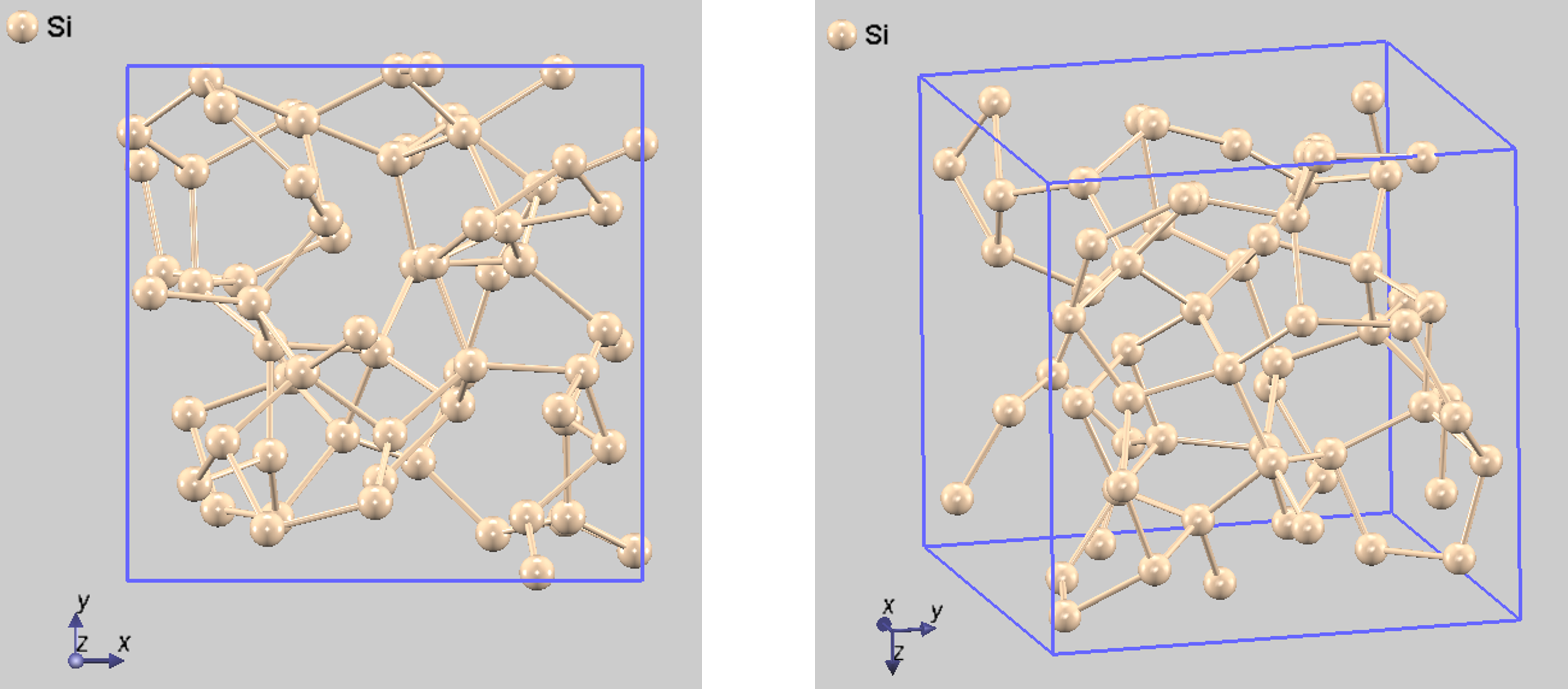図3. 計算で得られたアモルファスSiの安定構造（左：front view、右：perspective view）

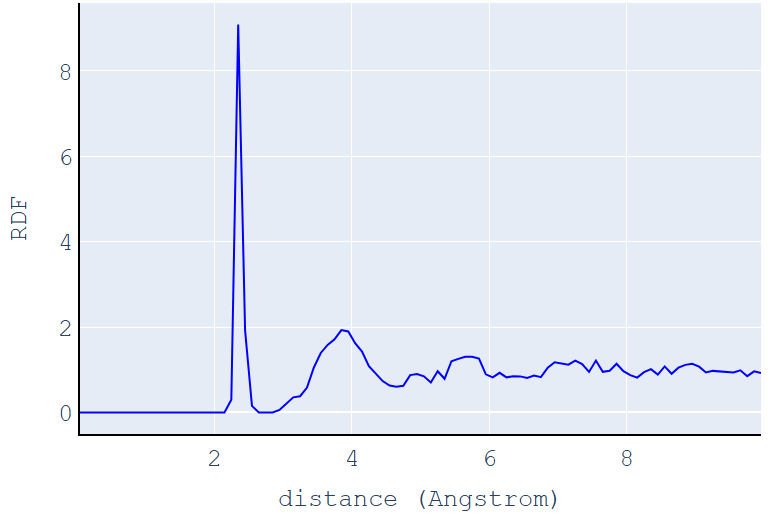図4. アモルファスSiのRDF計算結果

図4に示すように、本計算で得られたRDFは、明瞭な第一ピークと、それに続くブロードな第二、第三ピークを示しています。

短距離秩序: 第一ピークは約2.35 Å付近にあり、シリコン原子間の最近接距離（共有結合長）に対応します。この鋭いピークは、アモルファス構造においても原子の結合長という短距離の秩序が保たれていることを示しています。
長距離秩序の消失: 第二ピーク以降が非常にブロードであり、距離が離れるにつれてRDFが1に近づいていくことから、結晶のような長距離にわたる周期性（長距離秩序）は失われていることがわかります。

さらに、この計算結果は参考文献[3]のFig. 1に示されている実験データや他のDFT計算（a-Si219モデル）によるRDFとよく一致しています。特に第一ピークの位置（約2.35 Å）や第二ピークの位置（約3.8 Å）、そしてこれらのピークの形状を再現していることから、本シミュレーションによって、原子数が多いa-Si219モデルに近いアモルファスSiの原子構造モデルが構築できたと言えます。第一原理MDシミュレーションは計算コストが高いため、原子数を抑えつつ物理現象を適切に反映できる計算モデルの構築は非常に重要です。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEに実装された溶融急冷法シミュレーション機能を用いて、アモルファスシリコンの原子構造モデルを作成しました。エネルギープロファイルの経時変化から、高温の液体状態からの冷却・固化プロセスが、大きめの時間ステップでも効率的に進行したことを確認しました。さらに、得られた構造の動径分布関数（RDF）を算出したところ、アモルファス構造に特徴的な短距離秩序の存在および長距離秩序の消失が明確に示され、その形状は大きめのモデルを用いた先行研究や実験値ともよく一致しました。

参考文献#

L. Martínez, R. Andrade, E. G. Birgin, and J. M. Martínez, "Packmol: A package for building initial configurations for molecular dynamics simulations", Journal of Computational Chemistry 30, 2157-2164, 2009.
C. Chen and S. P. Ong, "A universal graph deep learning interatomic potential for the periodic table", Nature Computational Science 2, 718 (2022).
R. V. Meidanshahi, S. Bowden, and S. M. Goodnick, "Electronic structure and localized states in amorphous Si and hydrogenated amorphous Si", Phys. Chem. Chem. Phys. 21, 13248 (2019).