第一原理計算における構造最適化アルゴリズムの性能比較:BFGS法とXGDIIS法#

第一原理計算において、物質の安定な原子配置(平衡構造)を決定する「構造最適化」は、最も基本的かつ重要な計算ステップの一つです。この計算コストは系が大きくなるにつれて増大するため、より効率的(高速かつ安定的)なアルゴリズムが求められます。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、標準的な構造最適化アルゴリズムであるBFGS法やCG法に加え、GDIIS法、および独自に改良されたXGDIIS (eXtended Geometric Direct Inversion of Iterative Subspace)法に対して、複数の系でベンチマーク計算を実施し、その性能を比較します。
Keywords: 第一原理計算, 密度汎関数法 (DFT), 構造最適化, XGDIIS, BFGS, CG, GDIIS, Quenched MD
ベンチマークの計算モデルと計算条件#
各アルゴリズム [1-3] の性能を比較するため、特性の異なる以下の4つの系でベンチマークテストを行いました:
- ケース 1 : cis型のジクロロシクロヘキサン(分子)
- ケース 2 : ルチル型TiO2(バルク結晶)
- ケース 3 : SiO2(バルク結晶)
- ケース 4 : Si(001)表面、水素終端あり・なし(表面モデル)
図1に、各ケースで用いた構造モデルを示します。
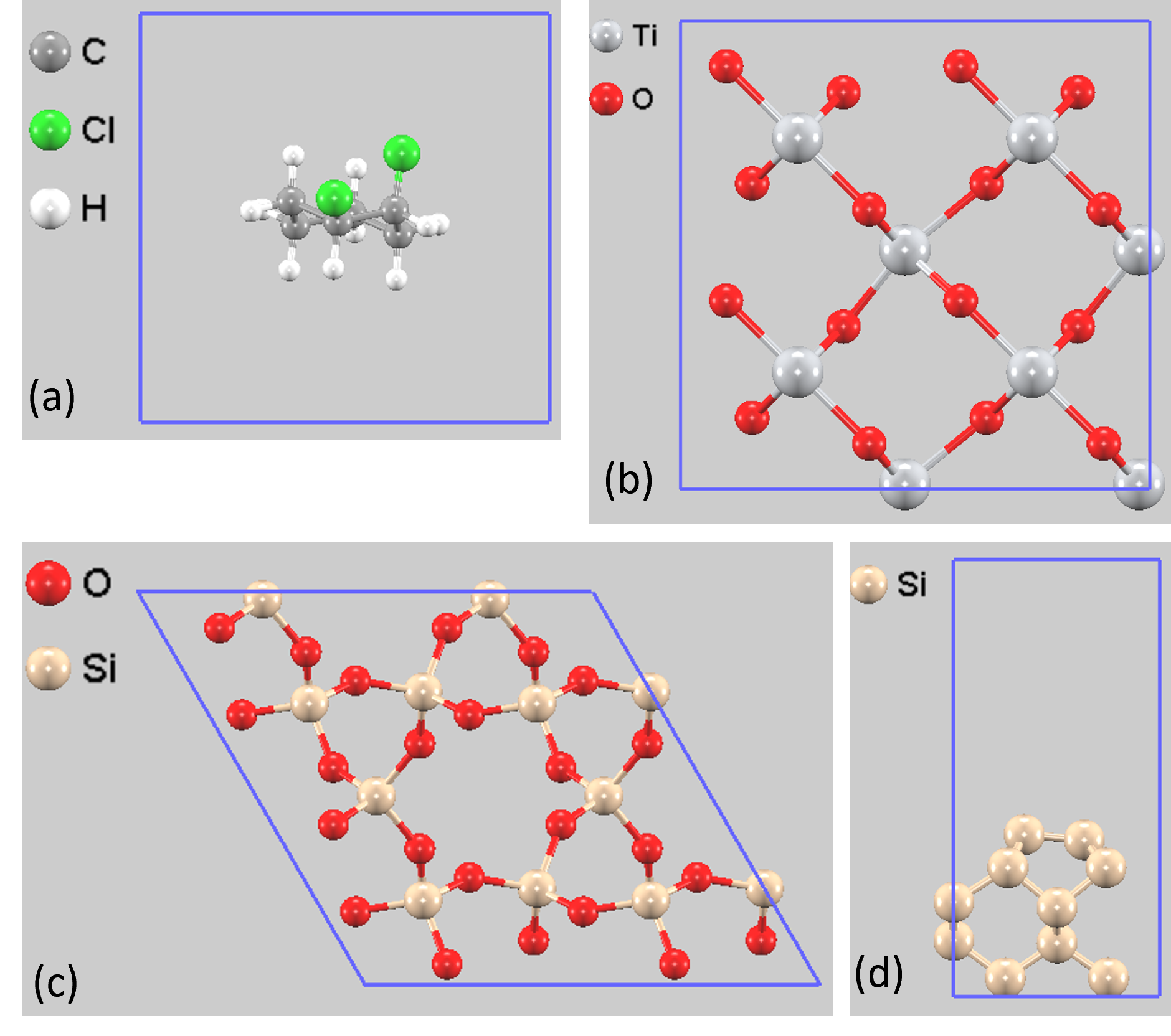
図1. ベンチマークに用いた各構造モデル。 (a) ジクロロシクロヘキサン(C6H10Cl2)分子、 (b)ルチル型TiO2、 (c) SiO2、 (d) Si(001)表面(水素終端なし)。視認性のため、TiO2とSiO2の2x2x2スーパーセルを表示しています。
本解析で用いた主な計算条件は表1に示されています。力の収束判定を 10-4 Hartree/Bohr という比較的厳しい条件に設定し、各手法がこの条件を達成するまでの反復計算回数を比較しました。
表1. ベンチマークの主な計算条件
| 項目 | 設定 |
|---|---|
| 力の収束判定 | 10-4 Hartree/Bohr |
| 電子状態計算の収束判定 | 10-10 Hartree (per atom) |
| 最大反復回数 | 200回(これを超えたら未収束とみなす) |
計算結果と考察#
水素終端Si(001)表面における収束挙動#
まず、バルク層に水素で終端したSi(001)(ケース4の1種)について、代表的な3つのアルゴリズム(XGDIIS [2], BFGS, CG)の収束挙動を比較しました(図2)。
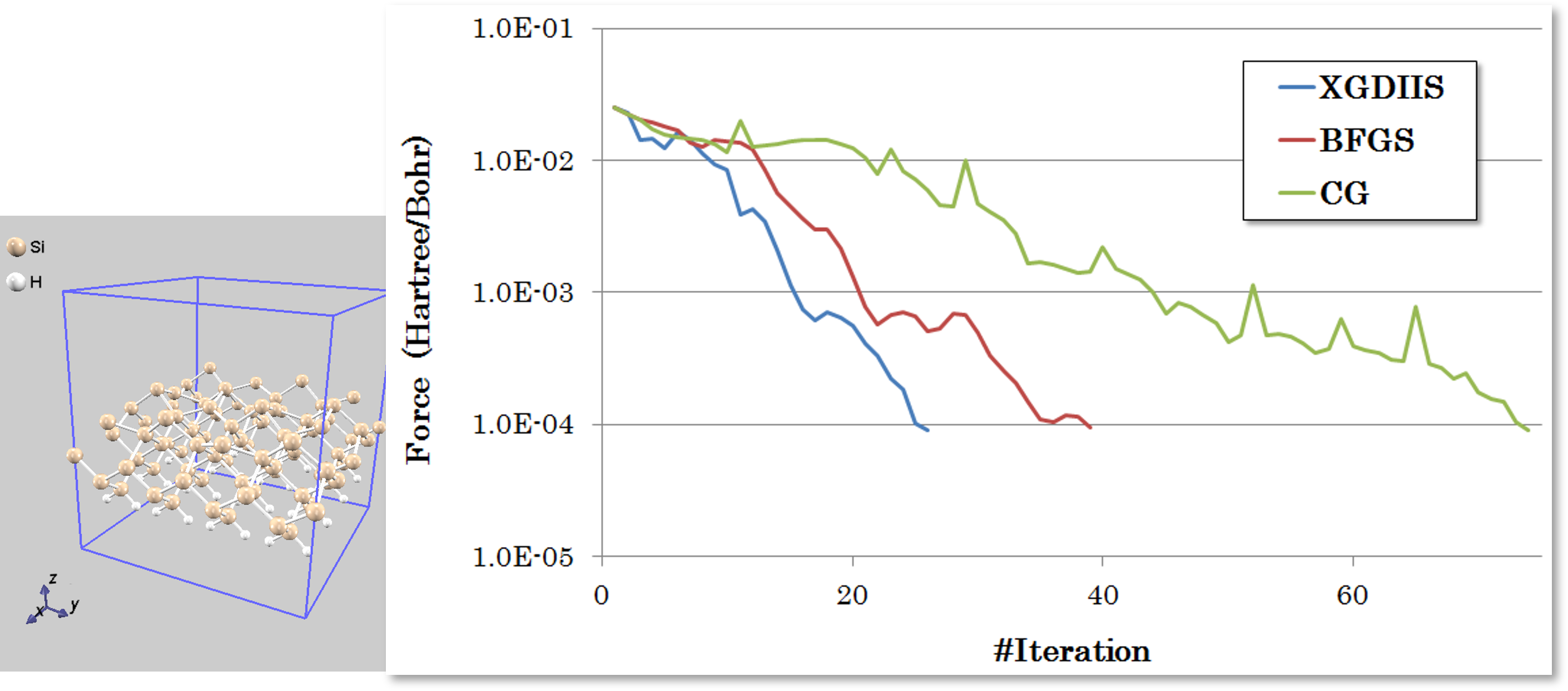
図2. 水素終端Si(001)表面における各最適化手法の収束履歴。縦軸は原子に働く力の最大値(対数スケール)、横軸は反復回数を示します。
図2から明らかなように、XGDIIS法(青線)は、BFGS法(赤線)やCG法(緑線)と比較して、最も速く力が減少していることがわかります。BFGS法も比較的速く収束していますが、XGDIIS法は約25回程度で収束判定(10-4 Hartree/Bohr)に達しており、より効率的です。一方、CG法は収束が著しく遅いことが示されています。
全ベンチマークケースにおける収束回数の比較#
次に、4つの全ケースについて、収束までに要した反復回数を表2にまとめます。Advance/PHASEでは、計算初期(力が大きい状態)と収束間際(力が小さい状態)で手法を切り替えるハイブリッド計算が可能です。この表では、Quenched MD法とCG法は単独で、GDIIS法、BFGS法、XGDIIS法はハイブリッド設定(初期はCG法やQuenched MD法を使用)で計算されています。
表2. 構造緩和法の違いによる収束にいたる回数の比較。200回を超えた場合は「未収束」。
| 手法 | ケース 1 (C6H10Cl2分子) |
ケース 2 (TiO2) |
ケース 3 (SiO2) |
ケース 4 (Si(001)、H終端なし) |
|---|---|---|---|---|
| Quenched MD | 未収束 | 115 | 166 | 未収束 |
| CG | 195 | 62 | 28 | 124 |
| GDIIS | 未収束 | 71 | 13 | 176 |
| BFGS | 87 | 38 | 16 | 67 |
| XGDIIS | 85 | 26 | 10 | 44 |
表2の結果から、以下のことが明らかになりました:
- Quenched MD法は非常に収束が遅く、2つのケースで未収束となりました。
- CG法は全てのケースで収束しましたが、回数は総じて多めです。
- GDIIS法はケース3(SiO2)でBFGSより速いでしたが、他のケースではBFGS法やCG法より遅く、ケース1では未収束となり、系の依存性が大きいことが示唆されます。
- BFGS法は全てのケースで安定して収束し、CG法よりも少ない回数で良好な結果を示しました。
- XGDIIS法は、全てのケースで最速の収束を達成しました。図2の水素終端Si表面での結果に加え、表2の4ケース(水素なしSi表面を含む)全てで高い安定性と収束性を持つことが確認されました。
補足:各最適化手法の特徴#
本解析で比較した各アルゴリズムは、エネルギーが最も低くなる安定構造を探すための代表的な手法です。それぞれに異なる戦略(得意・不得意)があります。
- Quenched MD (クエンチ法): 最も単純な手法の一つです。原子に働く力(エネルギーの勾配)の方向に原子を動かし、エネルギーの坂を真っ直ぐ下るイメージです。あるいは、原子を運動させ(動力学)、定期的にその速度をゼロに「クエンチ(冷却)」することで、エネルギーが低い位置を探します。力が非常に大きい計算の初期段階で有効です。
- CG (Conjugate Gradient, 共役勾配法): 坂を下る際に、現在の勾配方向だけでなく、「一つ前のステップで進んだ方向」の情報も利用(共役)します。これにより、単純な勾配法で起こりがちなジグザグな動きを抑え、より効率的に最小値(谷底)を目指します。大規模な系でもメモリ効率が良く、確実に安定構造へ到達させたい場合に適しています。
- GDIIS (Geometric Direct Inversion in Iterative Subspace, 幾何学的反復部分空間直接逆転法): 過去の複数のステップにおける「原子の座標」と「力(勾配)」の情報を記憶しておきます。これらの履歴データを組み合わせて、「次に勾配がゼロになりそうな最適構造」を予測(外挿)するインテリジェントな手法です。エネルギー曲面が非常に平坦になる収束の最終段階で、特に高い効率を発揮します。
- BFGS (Broyden–Fletcher–Goldfarb–Shanno): 準ニュートン法と呼ばれるカテゴリの、非常に強力な手法です。勾配(坂の傾き)だけでなく、エネルギー曲面の「曲がり具合(ヘシアン行列)」も考慮して進むべき方向を決定します。この「曲がり具合」をステップごとに近似的に更新していくため、計算コストを抑えつつ高速な収束を実現します。多くの場合、標準的かつ高性能な手法です。
- XGDIIS (eXtended Geometric Direct Inversion of Iterative Subspace): Advance/PHASEのデフォルト手法です。GDIIS法と準ニュートン法(BFGSなど)をベースに、安定性と収束性を高める改良が加えられています。最大の特徴は、計算状況に応じて他の手法(Quenched MD法など)と自動的に混合(ハイブリッド)することです。力が大きい初期はQuenched MD法の割合を多くし、力が小さくなるとXGDIIS法の割合を増やして一気に収束させます。XGDIIS法は、特にタンパク質のような巨大分子や表面系など、大規模系の最適化に有効です。
XGDIIS法とBFGS法が一般的な構造最適化に推奨されますが、どの方法も万能ではなく、対象とする系や構造によって収束性能が異なる場合があります。したがって、対象とする系(分子、バルク、表面など)の特性や、最適化の状況(力が大きい初期段階か、収束間際の段階か)を考慮して、最適なアルゴリズムを選択したり、あるいはXGDIIS法のように状況に応じて手法を自動で混合するハイブリッド法を活用したりすることが、計算効率を高める上で重要です。
まとめ#
本解析では、第一原理計算ソフトウェアAdvance/PHASEに搭載されている複数の構造最適化アルゴリズムについて、4種類の異なるベンチマークテストを実施しました。その結果、標準的なBFGS法や、GDIIS法と準ニュートン法をベースとしたXGDIIS法 が、分子、バルク結晶、表面系という特性の異なる代表的な系において、安定かつ効率的に収束できることが実証されました。これらの高性能な構造最適化アルゴリズムは、ナノ・材料系の第一原理シミュレーションに不可欠の手法となっています。
本解析の詳細や、研究への適用可能性に関するご相談はこちら
お問い合わせ参考文献#
- P. Császár and P. Pulay, "Geometry optimization by direct inversion in the iterative subspace", J. Mol. Struct. (Theochem) 114, 31 (1984).
- Ö. Farkas and H. B. Schlegel, "Methods for optimizing large molecules. Part III. An improved algorithm for geometry optimization using direct inversion in the iterative subspace", Phys. Chem. Chem. Phys. 4, 11 (2002).
- H. B. Schlegel, "Geometry optimization", Wiley Interdisciplinary Reviews: Computational Molecular Science 1, 790 (2011).
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学