第一原理MDを用いた液体の構造解析

経験的なポテンシャル関数を用いる古典分子動力学（MD）シミュレーションとは異なり、第一原理分子動力学（第一原理MD）シミュレーションは、原子間に働く力を量子力学（密度汎関数理論）に基づいて直接計算する手法です。これにより、ポテンシャル関数の開発が困難な複雑な系や、化学反応を伴う系、電子状態が物性に大きく寄与する液体金属などの解析が可能になります。本事例では、第一原理計算ソフトウェアAdvance/PHASEを用いて、代表的な液体である水（H₂O）と液体シリコン（l-Si）の第一原理MDシミュレーションを行い、その構造を解析します。

Keywords: 第一原理分子動力学, 液体, 構造解析, 動径分布関数, 配位数, 水, 液体シリコン

予備知識：動径分布関数と配位数

液体の構造を特徴づける重要な物理量として、動径分布関数 g(r) と配位数 N(r) があります。

• 動径分布関数 $g(r)$: ある原子を中心に見たとき、そこから距離 r の位置に他の原子が存在する確率を、系の平均密度で規格化したものです。g(r) > 1 であれば平均より原子が密に、g(r) < 1 であれば疎に存在することを示します。具体的には、距離 r と r+dr の間にある原子の数 n(r) を用いて、以下のように定義されます。

  $g(r) = \frac{V}{N} \frac{n(r)}{4\pi r^2 dr}$
  ここで V は系の体積、N は原子数です。長距離では原子の相関がなくなるため、g(r)は1に近づきます。

• 配位数 $N(R)$: ある原子から見て、半径 R 以内に存在する原子の平均個数を示します。動径分布関数 g(r) を積分することで、以下のように計算されます。

  $N(R) = 4\pi\rho_0\int_0^R r^2g(r)dr$
  ここで $\rho_0$ は、対象となる原子の平均数密度（N/V）です。通常、g(r) の第一ピークが終わる最初の谷（ミニマム）までの距離で積分することで、最近接原子の配位数を求めます。
  ※原子数 $N$ と配位数 $N(R)$ は、同じ記号$N$を使用していますが異なる物理量です。

解析事例1：水 (H₂O) の構造解析

分子性液体である水の構造を第一原理MDシミュレーションで解析し、水素結合に由来する特徴的な構造を動径分布関数と配位数から評価します。

計算モデルと計算条件

計算モデルとして、32個の水分子（水素原子64個、酸素原子32個）を含む立方晶セルを用いました。MDシミュレーションは、NVTアンサンブル（粒子数、体積、温度が一定）のもと、Nosé-Hooverサーモスタットを用いて温度を300 Kに制御しました。主な計算条件を表1にまとめます。

表1. 水の第一原理MDシミュレーションの主な計算条件

項目	設定値
組成	H 64個, O 32個 (H₂O 32分子)
密度	1.00 g/cm³
温度	300 K (Nosé-Hooverサーモスタット)
計算ステップ	11200ステップ (時間刻み: 0.7 fs)
汎関数	GGA-PBE
カットオフエネルギー	25 Rydberg

計算結果と考察

図1にMDシミュレーションにおける水分子の配置のスナップショットを示します。分子は液体特有の不規則な配置を取りつつも、分子間の水素結合によって絶えず変化するネットワーク構造を形成している様子が確認できます。

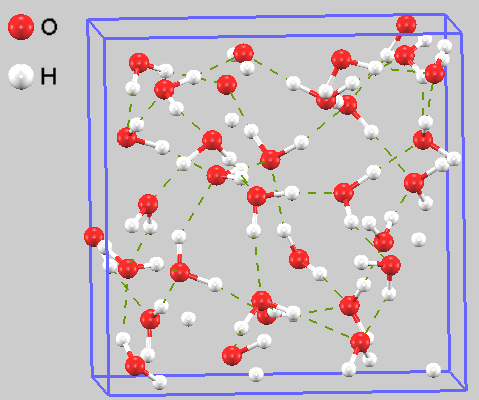
図1. 水の第一原理MDシミュレーションにおける原子配置のスナップショット。緑破線は水素結合を示しています。

図2は、第一原理MDシミュレーションから得られた水の動径分布関数 g(r) です。各曲線は、原子間の特徴的な距離における存在確率を示しています。

• g(O-H)（青線）: 約1.0 Åの極めて鋭いピークは分子内の共有結合、約1.8 Åのブロードなピークは分子間の水素結合に対応します。
• g(H-H)（オレンジ線）: 約1.6 Åのピークは分子内のH-H間距離、約2.4 Åのピークは隣接分子間のH-H間距離を反映しています。
• g(O-O)（緑線）: 約2.75 Åに現れる強い第一ピークは、水素結合で結ばれた水分子間の距離を示す最も重要な指標です。

これらのピーク構造は、液体でありながら水が明確な局所構造を持つことを示しています。

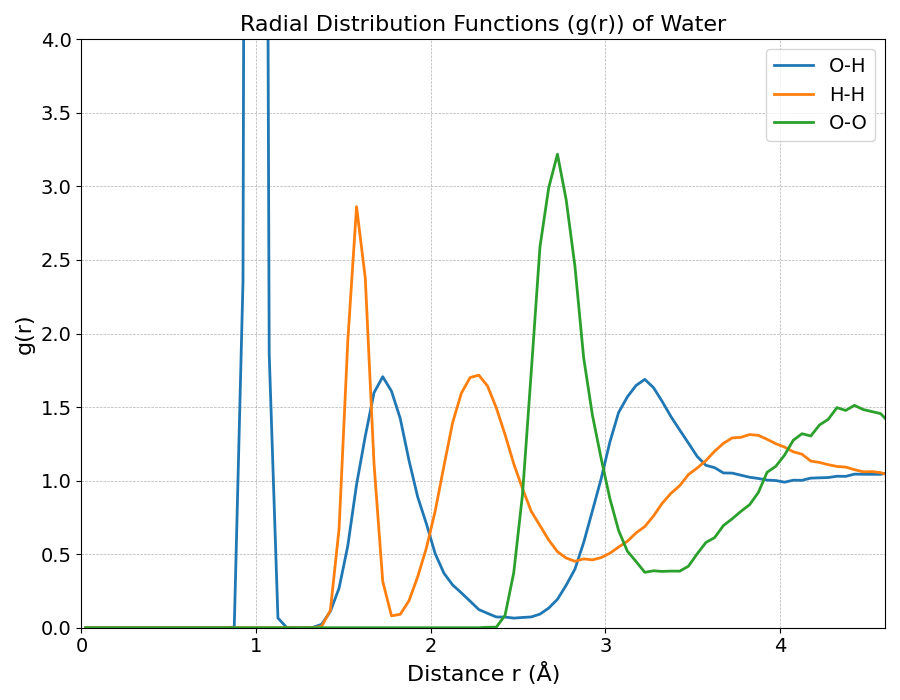
図2. 統計平均した水の動径分布関数

図3は、図2のg(r)を積分して得られた配位数 N(r) であり、中心原子から距離rまでに存在する相手原子の平均個数を示します。特に重要なのは、水分子の配位数を示すN(O-O)（オレンジ線）です。この値は、g(O-O)の第一の谷（約3.3 Å）の位置で約4のプラトーに達しており、これは液体の水が四面体的な水素結合ネットワークを形成していることの強力な証拠です。

また、N(H around O)（青線）が分子内結合距離で正確に2.0となっている点は、計算がH₂Oの化学量論を正しく再現していることを示します。これらの結果は実験値と非常によく一致しており [1]、本シミュレーションが水の複雑な構造を正確に捉えていることを裏付けています。

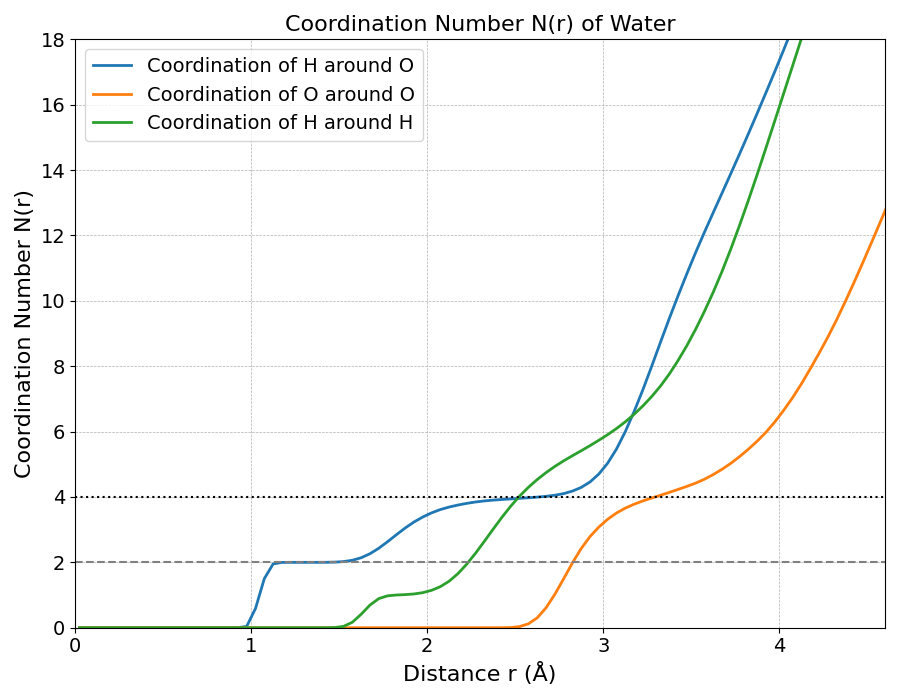
図3. 動径分布関数から計算した配位数。N(r)は水分子の配位数を示します。

解析事例2：液体シリコン (l-Si) の構造解析

固体では共有結合性の半導体であるシリコンが、液体状態では金属的な振る舞いを示すことはよく知られています。この構造変化を、第一原理MDシミュレーションを用いて動径分布関数と配位数から解析します。

計算モデルと計算条件

計算モデルとして、64個のシリコン原子を含む立方晶セルを用いました。計算の手続きとしては、まず2×2×2のスーパーセルを作成し、3,000Kで予備的なMD計算を行った。そこで得られた液体構造を初期原子配置とし、今度は融点付近である温度1,700KでのMDシミュレーションを行った。主な計算条件を表2に示します。

表2. 液体シリコンの第一原理MDシミュレーションの主な計算条件

項目	設定値
組成	Si 64個
密度	約2.58 g/cm³
温度	1700 K (Nosé-Hooverサーモスタット)
計算ステップ	6450ステップ (時間刻み: 3.0 fs)
汎関数	GGA-PBE
カットオフエネルギー	16 Rydberg

計算結果と考察

図4に液体シリコンの原子配置のスナップショットを示します。原子が不規則に配置され、液体状態であることがわかります。

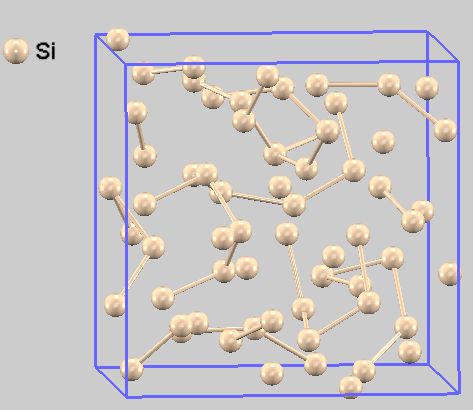
図4. 液体シリコンの第一原理MDシミュレーションにおける原子配置のスナップショット

図5に示す動径分布関数では、約2.43 Åに鋭い第一ピークが現れ、これは最近接原子間距離に対応します。それより遠距離ではピークがブロードになり急速に減衰しており、固体のような長距離秩序が存在しない液体状態であることが明確に示されています。実験データ [2]との比較として、計算したRDFは第一ピークが若干過小評価されている点をのぞけばRDFのピーク位置や形状をよく再現されています。

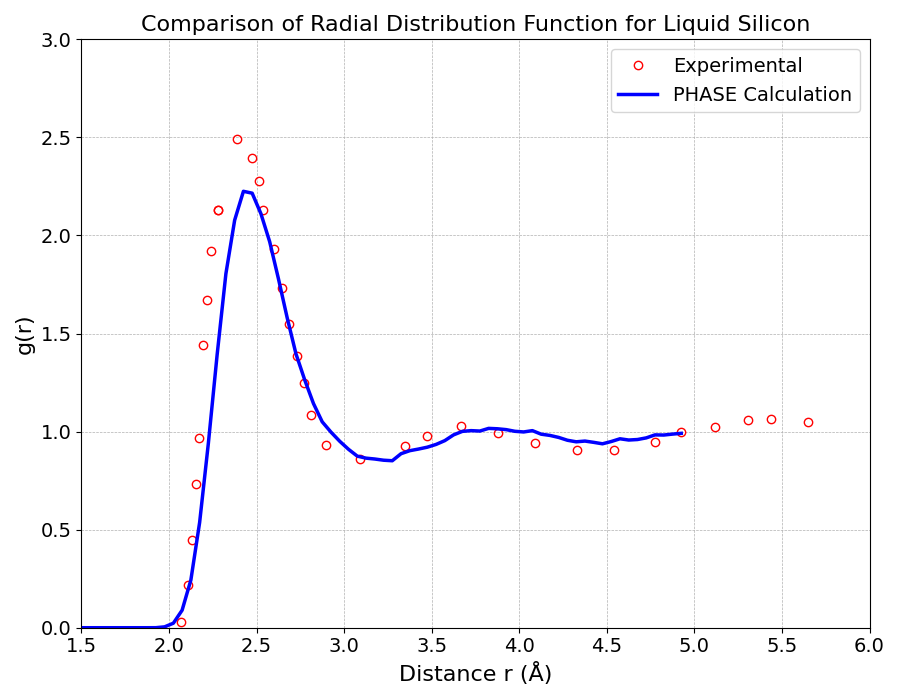
図5. 液体シリコンの動径分布関数 (丸：実測値、線：PHASE計算値）

液体シリコンの構造を理解する上で配位数が重要です（図6）。結晶シリコン（ダイヤモンド構造）の配位数は厳密に4ですが、本シミュレーションから得られた液体シリコンの配位数は、g(Si-Si)の第一谷（多項式フィッティングより約3.18 Å）まで積分すると約6.93となります。この値は、固体から液体になる際に配位数が大幅に増加するという、液体シリコンの重要な構造的特徴を正しく再現しています。参考文献 [3] で指摘されているように、実験 [2, 4] から得られる配位数自体も、その定義によって6から7の間の値をとることが知られています。他の第一原理計算では約6.4〜6.5という報告 [3, 5] もありますが、本解析の計算結果である6.93は、この「6〜7」という実験的なコンセンサスの範囲内に収まっています（実験のRDFに対するフィッティングで得られた配位数が6.88です）。

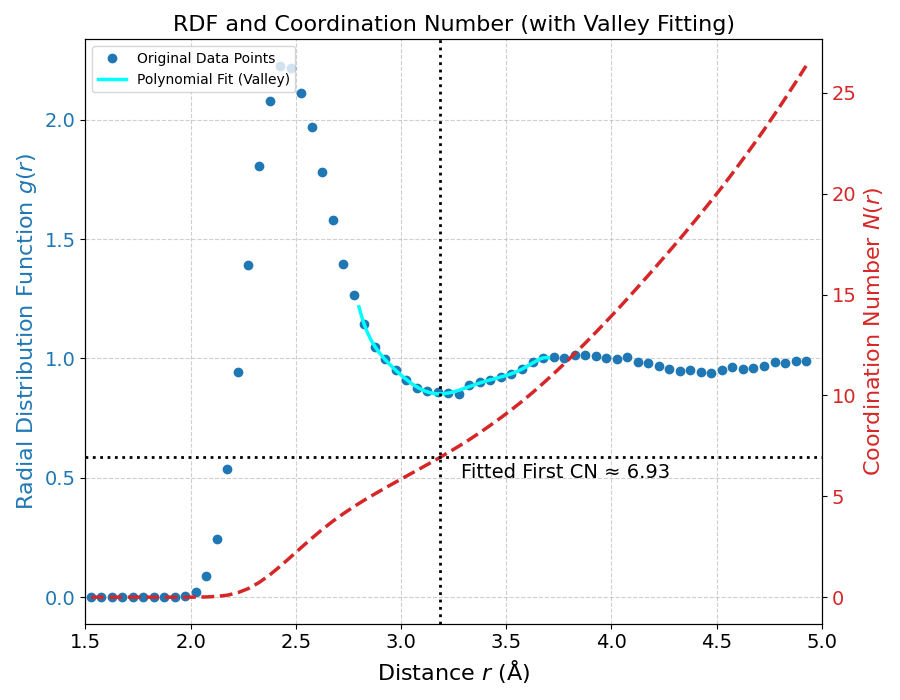
図6.　液体シリコンの動径分布関数 g(r) と配位数 N(r)。g(r)の第一谷（約3.18 Å）を多項式フィッティングで決定し、最近接配位数を6.93と算出しました。

まとめ

第一原理計算ソフトウェアAdvance/PHASEを用いた第一原理MDシミュレーションにより、水と液体シリコンの構造を解析しました。水の解析では、動径分布関数と配位数から、水素結合による特徴的な四面体ネットワーク構造を定量的に再現できました。液体シリコンの解析では、固体からの融解に伴い配位数が4から約6.93へと増加する構造変化を明らかにしました。これは、共有結合ネットワークが大きく崩れ、より高密度な金属性液体へ相転移することを示唆するもので、実験結果とも整合します。このように、第一原理MDシミュレーションは様々な液体の複雑な構造を高精度に予測できる強力な手法です。

参考文献

1. A. K. Soper, "The radial distribution functions of water and ice from 220 to 673 K and at pressures up to 400 MPa", Chem. Phys. 258, 121 (2000).
2. J. P. Gabathuler and S. Steeb, "Untersuchung von Schmelzen und amorphen Festkörpern mittels Neutronenbeugung", Z. Naturforsch. 34a, 1314 (1979).
3. I. Štich, R. Car, and M. Parrinello, "Bonding and disorder in liquid silicon", Phys. Rev. Lett. 63, 2240 (1989).
4. Y. Waseda and K. Suzuki, "Structure of molten silicon and germanium by X-ray diffraction", Zeitschrift für Physik B 49, 339 (1975).
5. J. R. Chelikowsky, N. Troullier, and N. Binggeli, "First-principles simulation of liquid silicon using Langevin dynamics with quantum interatomic forces", Phys. Rev. B 49, 114 (1994).

関連ページ

• 第一原理計算ソフトウェア Advance/PHASE
• 解析分野：ナノ・バイオ
• 産業分野：材料・化学