固体電解質ヨウ化銀の第一原理分子動力学シミュレーション#

PHASE logo

ヨウ化銀（AgI）は、特定の温度以上で銀イオン（Ag⁺）のみが結晶格子内を高速で移動する「超イオン伝導」と呼ばれる特性を示す、代表的な固体電解質です。この現象は、全固体電池などの次世代エネルギーデバイスへの応用において極めて重要です。本解析では、第一原理計算ソフトウェアAdvance/PHASEを用い、ヨウ化銀の第一原理分子動力学（MD）シミュレーションを実施します。これにより、固体電解質内でのイオンの動的な振る舞いを原子レベルで解明し、超イオン伝導のメカニズムを検証します。

Keywords: 第一原理分子動力学, 固体電解質, ヨウ化銀, 超イオン伝導, 拡散係数

計算手法#

本シミュレーションでは、系の温度を一定に保ちながら原子の運動を追跡する定温分子動力学（NVTアンサンブル）を用いました。この手法により、実験条件に対応する特定の温度（ここでは500K）での材料の挙動を再現できます。第一原理計算に基づいているため、原子間に働く力は量子力学的に計算され、経験的なポテンシャル関数を必要としません。これにより、特にイオンの移動や結合の再編成が起こるような複雑な現象を、高い信頼性でシミュレーションすることが可能です。

計算モデルと計算条件#

計算モデルとして、ヨウ化銀（AgI）の結晶構造情報 (cubic, α相)を基に作成した2×2×2のスーパーセルを用いました（図1）。このスーパーセルは、Ag原子16個とI原子16個から構成されます。図1には、計算に用いたスーパーセル（左）と、周期境界を考慮した際の結晶のつながりを視覚的に分かりやすくするため、隣接するセルの原子も表示したモデル（右）を示します。第一原理分子動力学（MD）シミュレーションは高コストであるため、本解析では計算コストを抑えつつ物理的な本質を反映できる計算条件を使用しました。

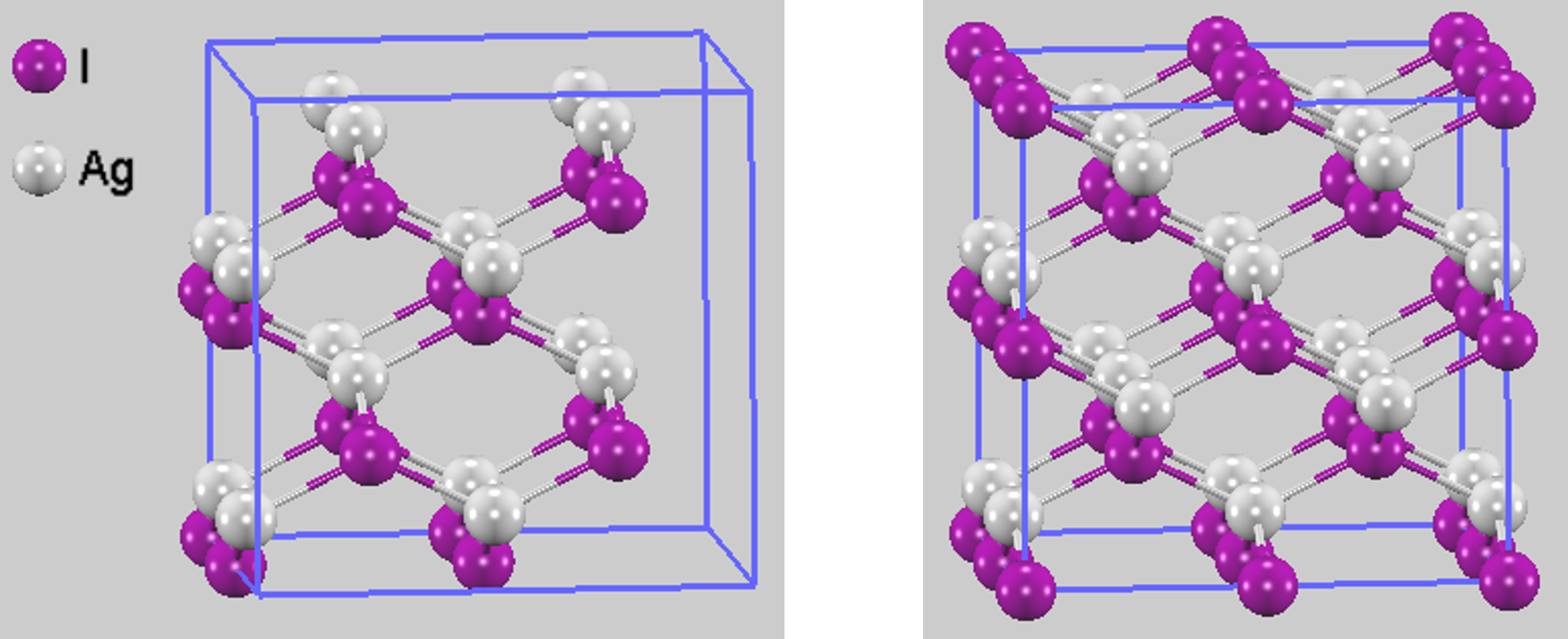
AgIの計算モデル
図1.　計算モデル（左：計算セル、右：境界原子を含むセル）。2×2×2のスーパーセルが用いられました。

表1.　計算条件

交換相関汎関数	GGA-PBE
カットオフエネルギー	波動関数： 16 Rydberg 電荷密度：150 Rydberg
k点サンプリング	Γ点のみ
温度制御	定温分子動力学（ターゲット温度 500K）
時間刻み	約8.5 fs

本解析では、計算コストと精度のバランスを考慮した計算条件を設定しました。例えば、波動関数のカットオフエネルギーは16 Rydbergと比較的小さく、時間刻みは約8.5 fsと一般的なMDシミュレーションよりも長く設定しています。これは、解析対象のヨウ化銀（AgI）が、銀（Ag）とヨウ素（I）という重い原子で構成されているためです。重い原子は、軽い原子に比べて①波動関数の空間変化が緩やかで、②原子の振動周期が長い、という特徴があります。そのため、それぞれ比較的小さなカットオフエネルギーと長い時間刻みを用いても、原子の挙動を物理的に妥当な範囲で追跡することが可能となり、計算コストを抑えつつ効率的なシミュレーションを実現しています。

計算結果と考察#

原子軌跡#

図2に、500 Kの温度条件下で行ったMD計算における原子の軌跡を示します。ヨウ素原子（紫色の点）は、初期の結晶格子位置を中心に小さく振動するにとどまっています。これは、ヨウ素イオンが安定した骨格構造を形成していることを意味します。一方で、銀原子（銀色の点）は、シミュレーション開始時の位置から大きく移動し、格子間を渡り歩くように結晶全体に広がっています。この結果は、Ag⁺イオンが液体のように振る舞い、I⁻イオンが形成する骨格構造の中を自由に動き回るという、超イオン伝導体の特徴的な挙動を視覚的に明確に捉えています。

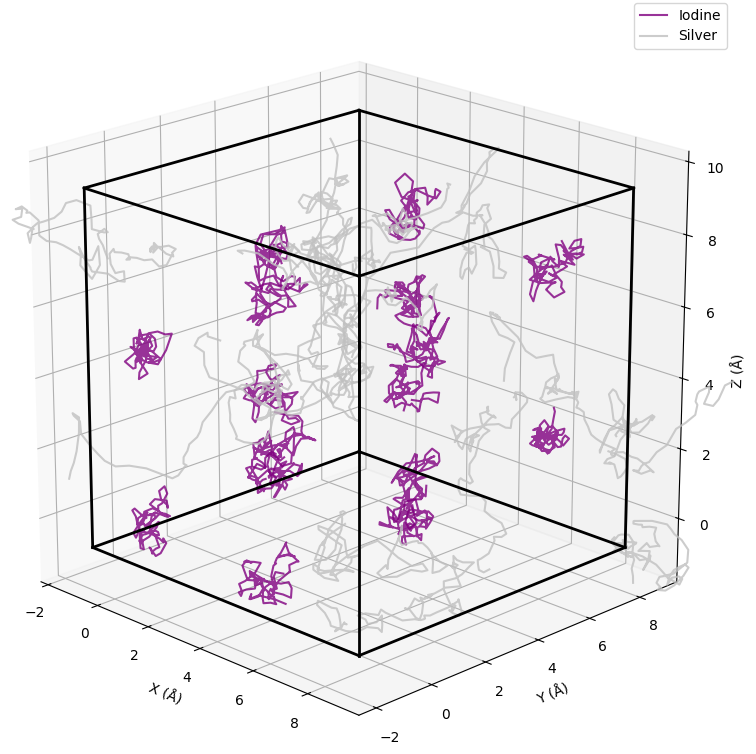
ヨウ化銀の原子軌跡
図2.　MD計算における原子軌跡（紫：ヨウ素、灰色：銀）

平均二乗変位(MSD)と拡散係数#

原子の移動を定量的に評価するため、各原子の平均二乗変位（Mean Square Displacement, MSD）を計算しました（図3）。MSDは、初期位置からの原子の移動距離の二乗平均であり、物質の拡散挙動を評価する重要な指標です。

ヨウ素（I）: MSDは一定の低い値の周りで飽和しており、時間と共に増加しません。これは原子が特定の格子点の周りで熱振動しているだけで、拡散していないことを示します。
銀（Ag）: MSDは時間経過にほぼ比例して直線的に増加しています。これは、銀原子がランダムウォーク的な運動、すなわち拡散を行っていることの明確な証拠です。

拡散現象において、MSDと拡散係数（D）の間には、アインシュタインの関係式が成り立ちます。3次元系では以下の式で表されます。

$\text{MSD}(t) = 6Dt$

この関係は、十分に時間が経過しMSDが時間に比例するようになった領域で成立します。MSDのグラフの傾きから銀の拡散係数を算出したところ、およそ $2.4 \times 10^{-5} \, \text{cm}^2/\text{s}$ という値が得られました。この値は、AgIが優れたイオン伝導性を持つことを定量的に裏付けるものです。

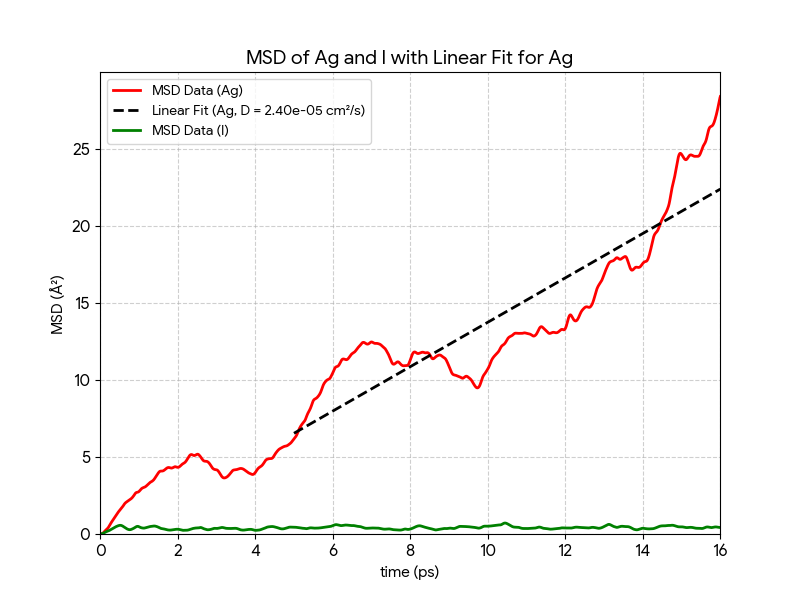
銀とヨウ素の平均二乗変位
図3.　銀（Ag）原子とヨウ素（I）原子の平均二乗変位（MSD）

文献値との比較#

本シミュレーションの妥当性を評価するため、算出された銀イオンの拡散係数を、過去に報告されている実験値や計算値と比較します。

手法	温度 (K)	拡散係数 D (10^-5 cm²/s)	文献
本解析	500	約 2.4	-
実験	498	1.85	[1]
古典MD	495	2.0	[2]
第一原理MD	500	約 2.5	[3]

本解析でMSDデータから直接算出した拡散係数 2.4 × 10^-5 cm²/s は、実験値 [1] とはやや差がありますが、古典MDでの計算結果 [2] に近い値が得られ、また、第一原理MDを用いた研究結果 [3] とも非常に近い値です。これらの比較から、本解析はヨウ化銀の超イオン伝導現象を良好に再現していることが確認できます。

まとめ#

本解析では、第一原理計算ソフトウェアAdvance/PHASEを用いて、代表的な固体電解質であるヨウ化銀（AgI）の第一原理分子動力学シミュレーションを行いました。その結果、500Kの温度下において、ヨウ素イオンが安定な骨格を形成する一方で、銀イオンがその骨格内を自由に拡散する「超イオン伝導」の状態を鮮明に再現することに成功しました。さらに、平均二乗変位の解析から銀イオンの拡散係数を定量的に評価しました。第一原理シミュレーションは、全固体電池をはじめとする新規材料の設計・開発において、強力なツールとなります。

参考文献#

A. Kvist and R. Tärneberg, "Self-diffusion of Silver Ions in the Cubic High Temperature Modification of Silver Iodide", Zeitschrift für Naturforschung A 25, 257 (1970).
M. Parrinello, A. Rahman, and P. Vashishta, "Structural Transitions in Superionic Conductors", Phys. Rev. Lett. 50, 1073 (1983).
B. C. Wood and N. Marzari, "Dynamical Structure, Bonding, and Thermodynamics of the Superionic Sublattice in α-AgI", Phys. Rev. Lett. 97, 166401 (2006).