第一原理計算による電子状態解析#

ナノ材料結晶の電子状態密度・バンド構造や格子定数・凝集エネルギー・体積弾性率などの基本的な物理量などは、Advance/PHASEを利用することによって簡単に得ることができます。以下にいくつかの結晶の計算例を、実験値とともにご紹介します。
金属の例:マグネシウム(Mg)結晶#
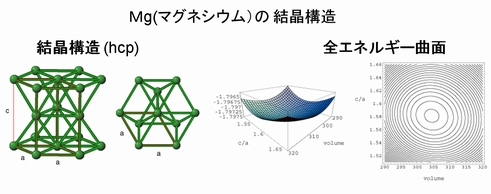
六方最密充填構造(hcp)をとるマグネシウム(Mg)結晶の計算事例をご紹介します。全エネルギー曲面計算より結晶構造の格子定数を求めました。さらに、凝集エネルギーEと体積弾性率Bを計算し、状態密度とバンド構造を解析しました。Advance/PHASEによる計算値は、シリコン(Si)結晶の同様、実験値と大変よく一致しています。


触媒の例:酸化チタンTiO2#
光触媒として注目されている酸化チタン(TiO2)は、温度・圧力など状態の違いにより、異なった結晶構造をとることが知られています。ここでは、酸化チタン(TiO2)の異なった2つの結晶構造:(I)ルチール型(正方晶高温型)と(II)アナターゼ型(正方晶低温型)の例をご紹介します。
Advance/PHASEで構造最適化計算を行うと、酸化チタンTiO2のどちらのタイプの結晶においても、格子定数の計算値と実験値は大変よく一致した結果が得られました。Advance/PHASEの第一原理計算は、異なった結晶構造を取りうる物質材料においても、その構造を高精度に予測することができます。


反強磁性体の例:クロム(Cr)#
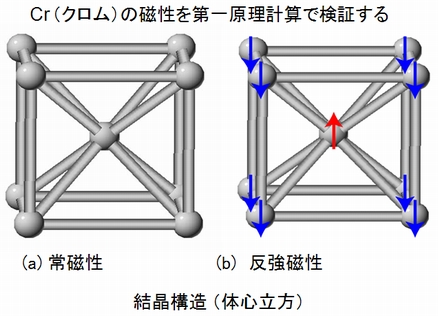
体心立方構造をもつクロム(Cr)の結晶は典型的な反強磁性体として知られています。Cr結晶の磁性(反強磁性)は、Advance/PHASEで正しく検証することができます。このことを示すために、体心立方構造をもつCr結晶に対して、常磁性と反強磁性の2つの異なった磁性で計算を行い、すでに知られているCr結晶の実験値と比較しました。
Advance/PHASEが材料の物性を正しく予測できるなら、反強磁性での計算結果は実験値とよく一致し、逆に、常磁性の計算結果は実験値と合わないはずです。
計算で求めた常磁性と反強磁性のCr結晶の格子定数はともに実験値と近い結果が得られ、常磁性および反強磁性のCr結晶の格子定数の値の違いからCrの磁性を判断することはできませんでした。
しかしながら、凝集エネルギーの値を比較したところ、反強磁性のCr結晶の値は常磁性の値より安定で、しかも、実験値と非常に近い値が得られました。従って、この第一原理計算より、Cr結晶の磁性が反強磁性であることが確認できました。


ハーフメタルの例:酸化クロム(CrO2)#
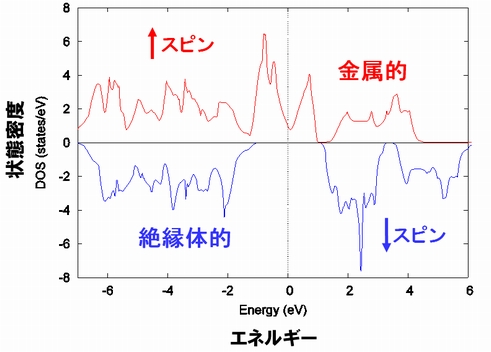
ルチール型構造をもつ酸化クロムCrO2は、電子スピンの偏極状態に依存して物性が変わるハーフメタルと呼ばれる特異な物質材料として知られています。ハーフメタルCrO2は、スピンが上向きの電子には金属、下向きの電子には絶縁体の性質をもつ物質です。
従って、この物質に電圧を印加すると、スピン偏極した電流が生じることになります。この特異的な物性を利用した材料開発が着目されています。Advance/PHASEで求めた酸化クロムCrO2のバンド構造は、電子スピン偏極によるハーフメタルの特異的な物性を正しく再現しています。

ストレステンソルの応用例:シリコン結晶の弾性率(弾性定数)#
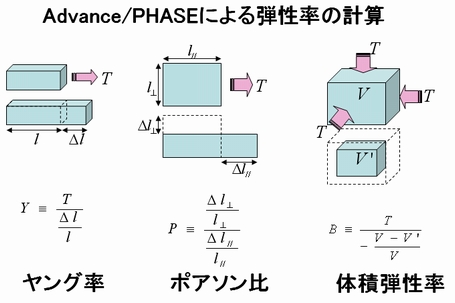
Advance/PHASEは、ナノ物質材料のストレステンソル(応力テンソル)を計算する機能があります。ストレステンソル(応力テンソル)は、物質に外部から力を加えたときに生ずる物質の歪みを表す物理量です。
ストレステンソルより、例えばヤング率、ポアソン比、体積弾性率などの弾性率(弾性定数)を計算することができます。Advance/PHASEで計算したシリコンSi結晶の弾性率の計算は、実測値と非常によく一致しています。

部分電荷密度計算の例:有機伝導体BEDT-TTF#
Advance/PHASEは、部分電荷密度計算よりバンド構造の部分領域を実際の原子構造中での電荷密度に変換することが可能で、さらに、その電荷密度をGUIプログラムで表示することができます。この機能を利用すると、例えば、結晶軸方向に対する伝導性の違いなどを解析することができます。
例として、炭素と硫黄原子を含んだ有機材料物質 (BEDT-TTF)2I3 [BEDT-TTF = Bis(ethylenedithio)tetrathiafulvalene ビス(エチレンジチオ)テトラチアフルバレン] の計算をご紹介します。(BEDT-TTF)2I3は指向性のある伝導物質として知られており、図で示した結晶軸の横軸方向は非伝導的で(絶縁体的な物性を示す)、縦軸方向には伝導性があります。
このような物質伝導の指向性は、Advance/PHASEの部分電荷密度計算から検証することができます。この有機伝導体のバンド計算を行いフェルミ面より上の部分領域に対応する電荷密度を求めると、図に示したように、結晶の縦軸方向に電荷密度がつながり、横軸方向にはつながっていない電荷密度が得られました。
この計算結果は縦軸方向は伝導的、横軸方向は非伝導的であることを示しており、Advance/PHASEで求めた(BEDT-TTF)2I3の伝導性は、実際の物性を正しく再現しています。

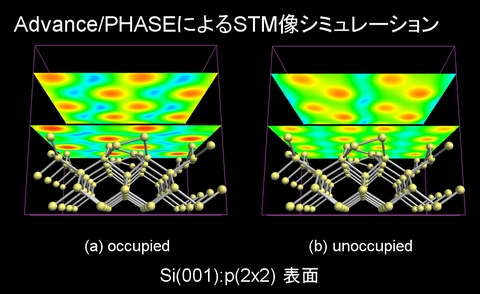
部分電荷密度計算の例:STM(走査型トンネル顕微鏡)像の解析#
Advance/PHASEの部分電荷密度計算機能より、STM(走査型トンネル顕微鏡)像をシミュレーションすることができます。図に示したのは、Advance/PHASEで計算したシリコン(Si)結晶のp(2×2)表面から1Å離れた場所と5Å離れた場所での占有状態の像と非占有状態のシミュレーション像です。
実験測定で得られたSTM像とAdvance/PHASEで計算されたシミュレーション像を比較して、物質の構造や電子状態を精密に解析することができます。
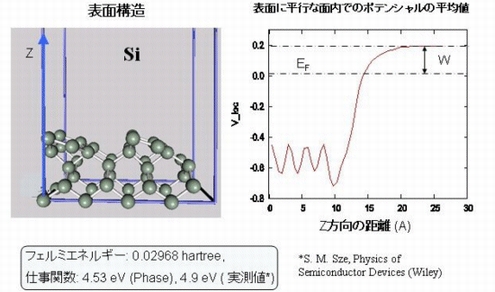
仕事関数#
仕事関数は、真空準位とフェルミ準位の差です。真空準位を表面から充分離れた(~10Åくらい)場所での局所ポテンシャルから見積もることによって仕事関数を求めることができます。シリコン結晶の計算例をご紹介します。Advance/PHASEで求めた計算結果は実験値と非常によく一致しています。
誘電関数・誘電率#
Advance/PHASEは、誘電関数や誘電率の計算を行うことができます。誘電関数ε(ω)は、物質に外部電場ωが加えられたときの物質の分極の応答です。物質の誘電率εは外部電場がゼロのときの誘電関数の値です。誘電関数を元に、屈折率や反射率などの光学定数(光学スペクトル)を計算することができます。
Advance/PHASEの誘電率計算は電子系からの寄与だけでなく、ベリー位相分極理論に基づいて格子系からの寄与も考慮にいれて計算することができますので、より精度の高い誘電率を求めることができます。
シリコンの誘電関数#
Advance/PHASEで計算したシリコン結晶の誘電関数を、実測値とともに図示します。計算値と実測値は、よい一致を示しています。なお、ここでは誘電関数の虚部ε2をバンド計算より求め、実部ε1をクラマース・クローニッヒの関係式より、ε2から変換して求めています。

金の誘電関数・反射率#
Advance/PHASE付属の擬ポテンシャルはすべて相対論効果を考慮して作成されています。相対論効果の重要性を示す一例として金(Au)の誘電関数の虚部ε2と反射率を、相対論効果を考慮した場合と考慮しない場合で計算を行いました。
図に示しましたように、明らかに、相対論効果を入れた計算のほうが、入れない計算よりも、実測値と一致しています。この計算より、相対論効果を考慮しないと可視光領域の光はすべて反射し、金は金色という結果が得られないことが分かります。1

1 Advance/PHASEでは、相対論効果を考慮しない計算を行うことはできません。
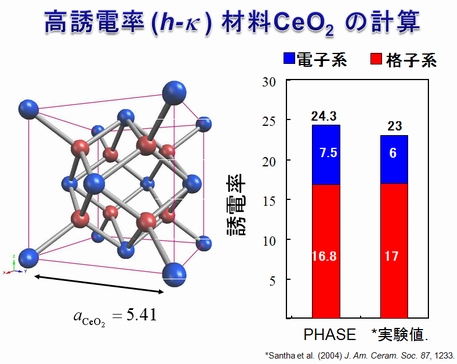
セリウム酸化物の誘電率#
セリウム酸化物CeO2は高誘電率材料として知られています。電子材料の誘電率を評価する際には、電子系および格子系両方からの寄与が重要です。Advance/PHASEの誘電率計算は、電子系と格子系からの寄与をそれぞれ独立に求めることができます。
計算結果より、セリウム酸化物CeO2の誘電率は格子系の寄与が非常に大きいことが明らかとなり、実験値とも非常によく一致しています。
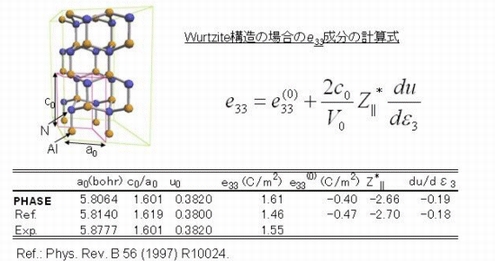
圧電定数#
Advance/PHASEでは、ベリー位相分極理論を応用して、圧電定数の計算ができます。圧電定数は、物質に外力(応力)が加わったときに誘起される分極を表す物理量です。計算例として、セラミックスの一種で、圧電材料として知られる窒化アルミニウムの圧電定数の計算値を実験値とともに示します。Advance/PHASEで求めた計算値と実験値は大変よく一致しています。
触媒反応解析#
ナノ材料の表面に原子を吸着させて構造緩和すれば、吸着や触媒反応のシミュレーションができます。触媒材料の開発に、第一原理計算が活用できます。
吸着時の全エネルギーから単体の原子(あるいは分子)、単体の表面の全エネルギーの和を引くことによって吸着エネルギーを得ることができます。Pt(100)表面の水素吸着エネルギーの計算結果から、水素分子のPt基盤への吸着物性を予測することができます。


原子分割局所状態密度:空孔のあるシリコン結晶#
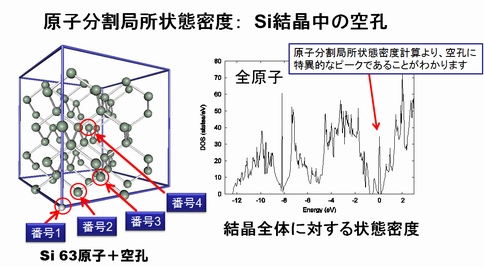
Advance/PHASEの原子分割局所状態密度計算機能の例として、空孔のあるシリコン結晶(Si63+空孔)の計算をご紹介します。空孔の存在が全体の状態密度に与える影響は、結晶全体の状態密度からすぐに理解することはできません。
Advance/PHASEの原子分割局所状態密度計算では、結晶中の各原子(あるいは空孔)座標での状態密度を個別に切り出すことができます。したがって、この計算機能を用いると、空孔が全体の状態密度に与える影響を直接調べることができます。
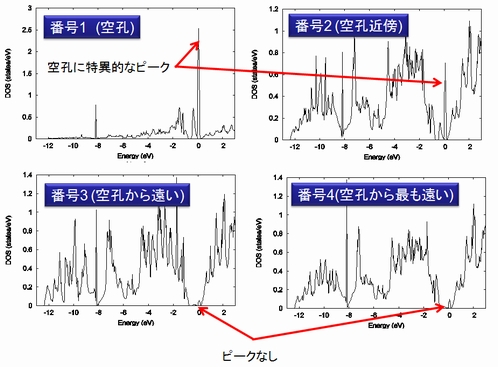
図に示したのは、空孔(番号1)、その近傍(番号2)、空孔からやや遠いSi原子(番号3)と、空孔から最も遠いSi原子(番号4)の位置での原子分割局所状態密度です。結晶全体の状態密度は、エネルギーが0 eVにピークがあります。
このピークは、原子分割局所状態密度計算より、空孔によって生じたピークに帰属することができます。また、空孔から離れていくにしたがって、局所状態密度は結晶全体の状態密度に近くなっていることもわかります。
このように、原子分割局所状態密度計算を活用すると、結晶中の各原子(あるいは空孔)が全体の状態密度に与える影響を詳細に調べることが可能です。
関連ページ#
- 第一原理計算ソフトウェア Advance/PHASE
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学