コンテンツにスキップ

Calculation Speed Benchmark of the Deep Learning Kinetic Energy Functional AdvanceSoft25#

Kohn-Sham DFT (KS-DFT), the most widely known method for Density Functional Theory (DFT) calculations for material property prediction, faces a challenge: because it requires the use of electron orbitals, its computational cost scales approximately as with respect to the system size. Orbital-Free DFT (OF-DFT) was proposed as a computational method to solve this problem. By directly optimizing the electron density without using orbitals, OF-DFT's computational cost scales as , enabling high-speed calculations for large systems.

However, a problem with conventional OF-DFT was the lack of a known kinetic energy functional with accuracy sufficient for practical use. To address this, AdvanceSoft Corporation developed the deep learning kinetic energy functional AdvanceSoft25 (AS25), which applies a proprietary "field-deepening" algorithm, and integrated it into Advance/OF-DFT. While maintaining the computational cost, the primary advantage of OF-DFT, AS25 achieves more accurate electron density calculations than conventional kinetic energy functionals (for details on calculation accuracy, please refer to the article here).

In this case study, we conducted a benchmark of the calculation speed of the deep learning kinetic energy functional AdvanceSoft25.

Calculation Conditions#

As the calculation target, we created supercell models by isotropically scaling an fcc Al structure file (mp-134) obtained from the Materials Project.

We performed KS-DFT and OF-DFT for each supercell under the following conditions and measured the calculation time.

KS-DFT Calculation Conditions

  • Wave function cutoff energy: 540 eV
  • Energy convergence threshold: ~ 1×10-7 eV
  • Eigenvalue solver: Davidson
  • k-point sampling: 0.05 Å-1

OF-DFT Calculation Conditions

  • Wave function cutoff energy: 540 eV
  • Energy convergence threshold: ~ 3×10-3 eV/atom
  • Optimization algorithm: CG-HS
  • Preconditioner: damping function (cutoff radius = 0.265 Å) 1

We used Quantum ESPRESSO 6.7 (AdvanceSoft modified version) for the KS-DFT calculations. For the OF-DFT kinetic energy functional (KE functional), in addition to AS25, we performed calculations using the existing well-known functionals TFλvW, LKT, and HC.

The specifications of the computer used in this study are shown below.

  • CPU: Intel Xeon Gold 6330 @ 2.00GHz
  • Number of CPUs used: 24 (12 cores × 2 CPUs)
  • Memory used: 128 GB (8GB DDR4-3200 RDIMM × 16)

Calculations were performed using MPI parallelization (24 processes) for KS-DFT and OF-DFT (excluding AS25), and OpenMP parallelization (24 threads) for AS252.

Calculation Results#

The following table and graph show the number of atoms in each supercell and the calculation time for each method. The values in parentheses in the table and the dotted lines in the graph are predicted values based on fitting3. Note that in this study, KS-DFT was not performed for structures with 500 or more atoms due to time constraints. Additionally, the calculations for AS25, TFλvW, LKT, and HC stopped due to insufficient memory at 2048, 6912, 6912, and 5324 atoms, respectively.

Number of Atoms KS (sec) AS25 (sec) TFλvW (sec) LKT (sec) HC (sec)
4 0.77 1.59 0.08 0.09 0.66
32 16.93 7.73 0.15 0.20 2.01
108 229.98 20.40 0.45 0.73 6.21
256 2283.35 40.72 0.99 1.59 12.71
500 (1.7×104) 91.99 2.00 3.40 25.99
864 (8.8×104) 160.79 3.31 6.00 43.61
1372 (3.5×105) 222.00 4.57 8.80 61.73
2048 (1.2×106) (347.96) 8.13 14.06 100.43
2916 (3.4×106) (495.43) 12.22 21.52 156.88
4000 (8.7×106) (679.60) 20.59 29.50 212.08
5324 (2.1×107) (904.55) 28.79 42.89 (277.91)

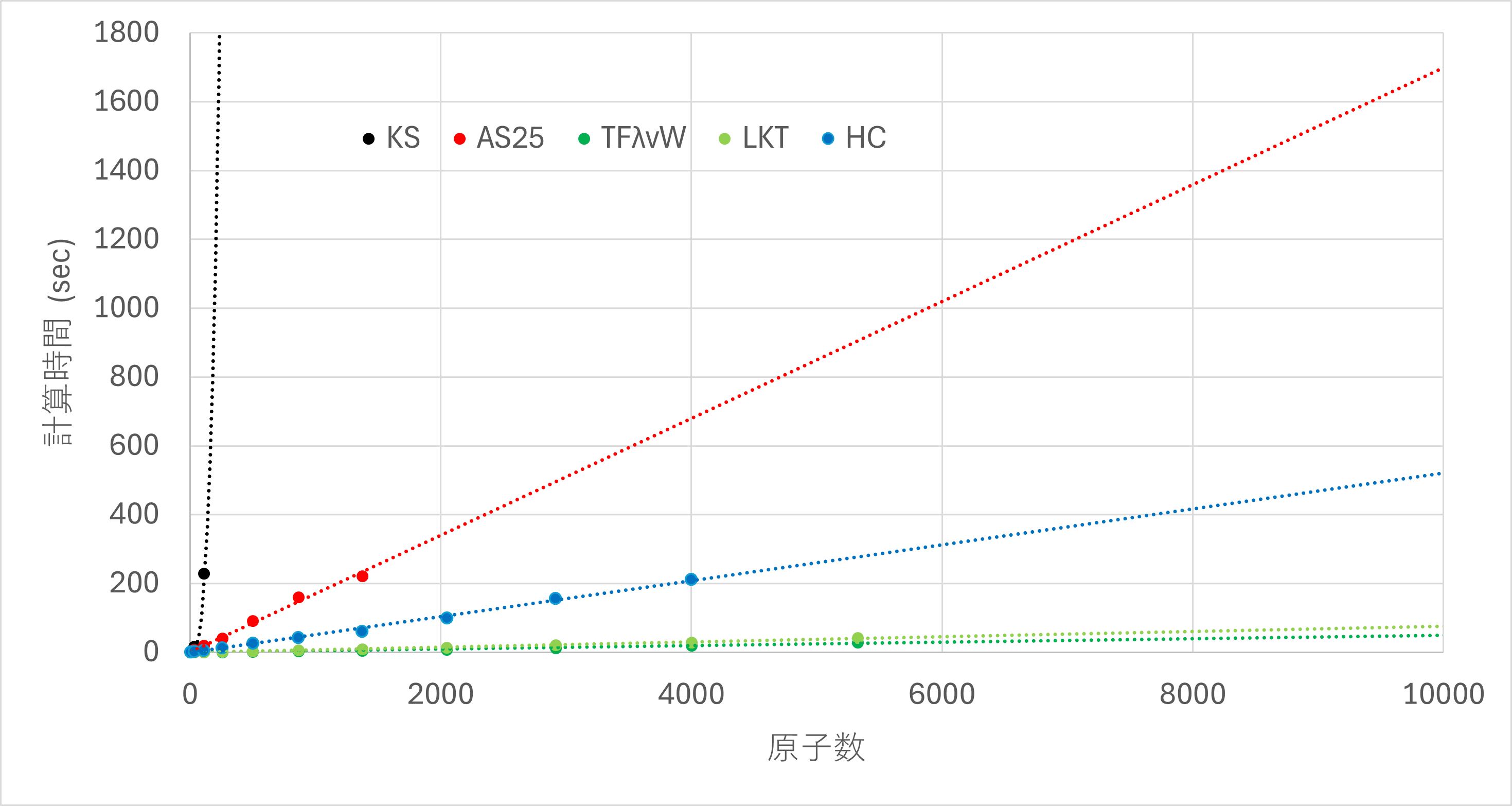
The results above show that for KS-DFT, the calculation time increases explosively as the number of atoms increases. For KS-DFT, the predicted calculation time reaches 8.8×104 seconds (~1 day) for 864 atoms, and 2.1×107 seconds (~244 days) for 5324 atoms, making it effectively impossible to compute.

On the other hand, for AS25, the calculation time increases linearly with the number of atoms and is overwhelmingly faster than KS-DFT. At 864 atoms, the calculation time is 160.79 seconds, and it is predicted that even for 5324 atoms, the calculation will complete in about 900 seconds.

Although AS25, which only supports thread parallelism (OpenMP), is slightly slower than conventional KE functionals that support MPI parallelization, considering its superior calculation accuracy, AS25 can be considered the most practical choice for large systems with several thousand atoms or more.

Furthermore, AS25 supports calculations using GPUs, which will enable even faster computations on GPU machines.

Conclusion and Outlook#

The results of this study show that OF-DFT calculations using our in-house developed deep learning kinetic energy functional, AdvanceSoft25, can perform electron density calculations overwhelmingly faster than KS-DFT, even for large systems with over 1000 atoms.

With KS-DFT, it is extremely difficult to calculate systems of several thousand to tens of thousands of atoms or more within a realistic timeframe because the calculation time increases as . In contrast, with OF-DFT using AS25, it is believed that high-speed calculations for large systems of over 10,000 atoms can be completed in a matter of hours, simply by using a machine with a larger memory capacity.

Moreover, we plan to support MPI parallelization for AS25 in the future, which is expected to lead to further speed improvements.

関連ページ#

  1. The preconditioner is an operator implemented by our company to suppress the high-frequency noise known to be present in the functional derivative of machine learning kinetic energy functionals. ↩

  2. For KS-DFT, the number of k-point parallels was set to 8. ↩

  3. We performed fitting on the measured values assuming that the calculation time is proportional to the cube of the number of atoms for KS-DFT and to the first power for OF-DFT. ↩