Accuracy Benchmark of the Deep Learning Kinetic Energy Functional AdvanceSoft25#

Kohn-Sham DFT (KS-DFT), the most widely known method for Density Functional Theory (DFT) calculations for material property prediction, faces a challenge: because it requires the use of electron orbitals, its computational cost scales approximately as $O(N^3)$ with respect to the system size. As a method to solve this challenge, Orbital-Free DFT (OF-DFT) calculation, which directly optimizes the electron density without using orbitals, has been proposed, and this calculation can be performed with Advance/OF-DFT. By not using orbitals, OF-DFT's computational cost scales as $O(N)$ , enabling high-speed calculations even for large systems.

However, conventional OF-DFT had not reached practical application because a kinetic energy functional with sufficient accuracy, which significantly affects calculation precision, was not known. To address this, AdvanceSoft Corporation developed the deep learning kinetic energy functional AdvanceSoft25 (AS25), which applies a proprietary "field-deepening" algorithm, and integrated it into Advance/OF-DFT. While maintaining the low $O(N)$ computational cost—the primary advantage of OF-DFT—AS25 enables more accurate electron density calculations than conventional kinetic energy functionals.

In this case study, we conducted a benchmark of the calculation accuracy of the deep learning kinetic energy functional AdvanceSoft25.

Calculation Conditions#

The target structures are 129 crystal structures, including metals, insulators, and slabs, which were separated as test data from the AS25 training dataset¹.

We performed KS-DFT and OF-DFT for each structure under the following conditions and calculated the error with respect to KS-DFT for the electron density distribution, total energy, formation energy, and surface energy.

Wave function cutoff energy: 1350 eV
Energy convergence threshold: 1×10^-4 eV
Maximum number of SCF steps: 200
Pseudopotential: OEPP (for 27 elemental species²)
Exchange-correlation functional: LDA
k-point sampling: 0.05 Å^-1 (KS-DFT)
Smearing width: ~ 0.7 eV ³ (KS-DFT)
Preconditioner: damping function (cutoff radius = 0.25 Å) ⁴ (OF-DFT)

We used Quantum ESPRESSO 6.7 (AdvanceSoft modified version) for the KS-DFT calculations. For the OF-DFT kinetic energy functional (KE functional), in addition to AS25 and the existing well-known functionals TFλvW, LKT, and HC⁵, we also used a non-local model NL25 and a semi-local model SL25 for comparison. These were trained using the AS25 architecture but without the field-deepening component.

Calculation Results#

Prediction Accuracy of Electron Density Distribution#

The Normalized Mean Absolute Error (MAE) of the electron density, defined by the equation below, was calculated for each structure. The average values for each material system are shown in the bar graph below.

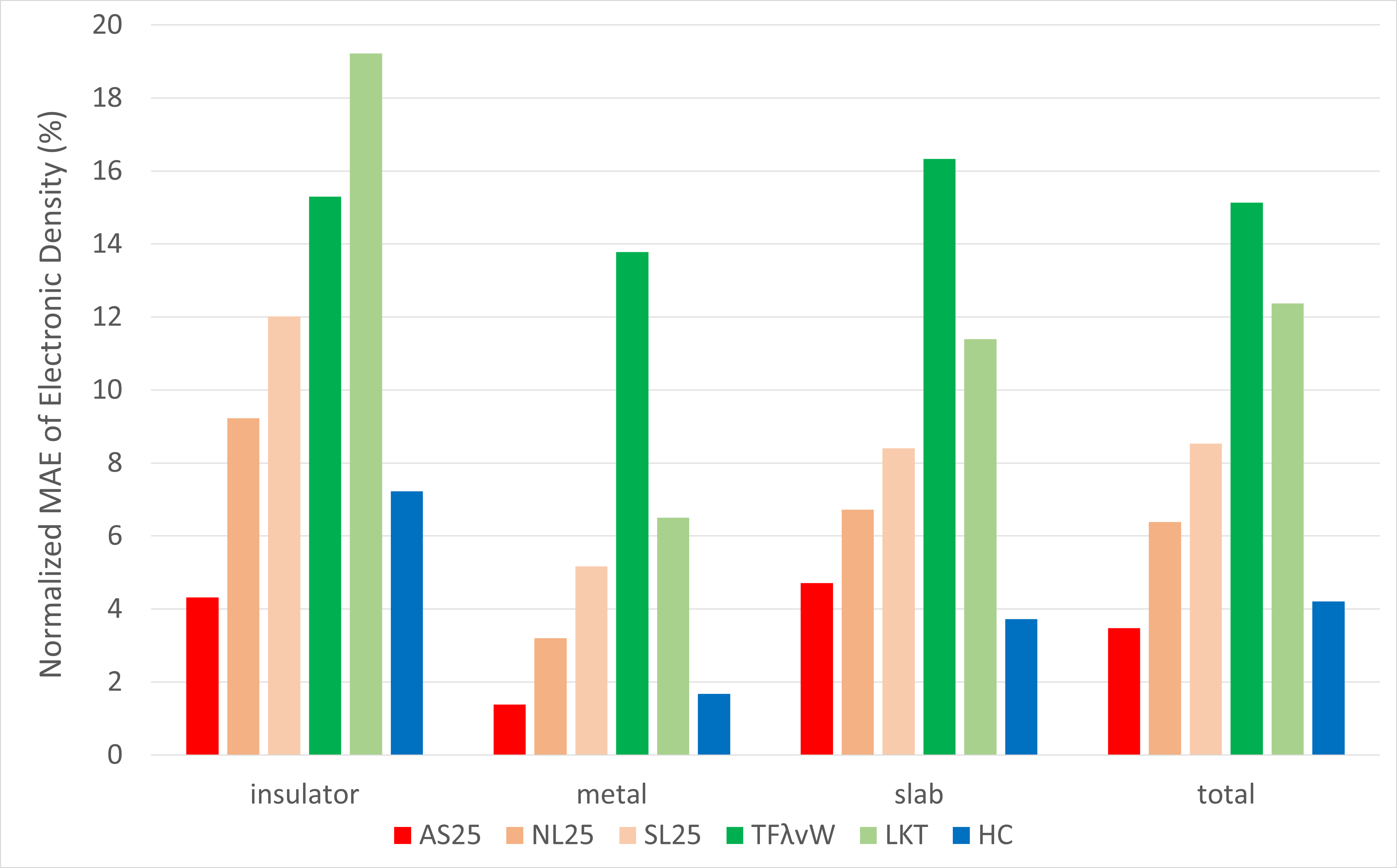
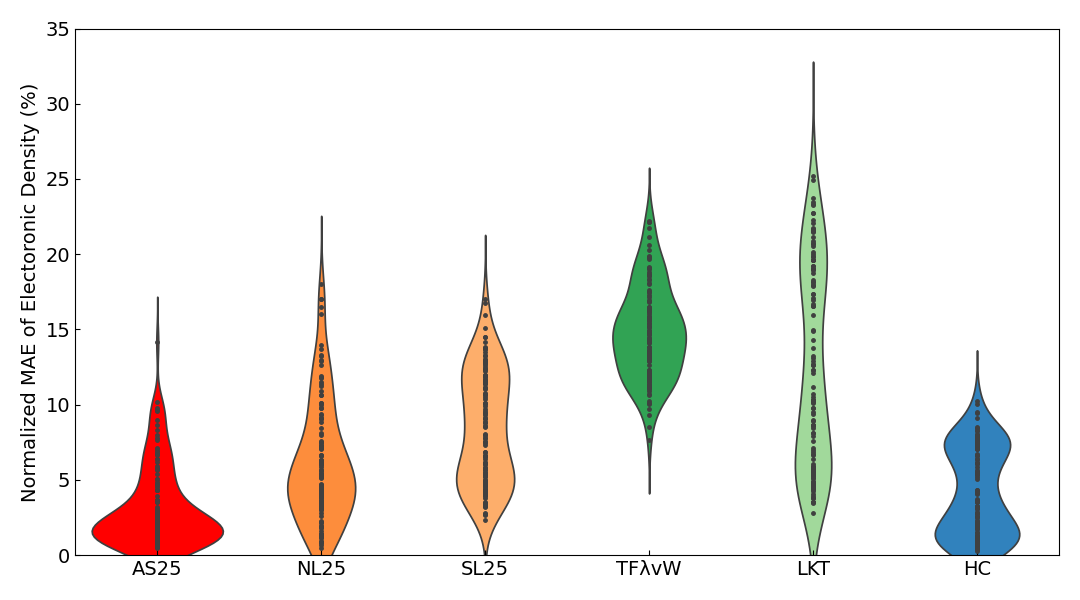
$\mathrm{Normalized\ MAE} = \frac{\sum_{i}^{n} | \rho^\mathrm{OF-DFT} (\boldsymbol{r}_i) - \rho^\mathrm{KS-DFT} (\boldsymbol{r}_i) |/n}{\sum_{i}^{n} \rho^\mathrm{KS-DFT} (\boldsymbol{r}_i)/n}$

Looking at the results for all systems, AS25 has the smallest Normalized MAE at about 3%, demonstrating superior electron density prediction accuracy compared to any of the conventional KE functionals. Furthermore, when compared to the non-field-deepened models NL25 and SL25, AS25's error is roughly less than half, indicating that field-deepening significantly contributes to the accuracy improvement.

It is known that conventional KE functionals have lower calculation accuracy for insulators, which have a band gap, compared to metals. This trend is indeed present in our results, with even the best conventional KE functional, HC, having an error of about 7%. In contrast, while AS25 shows a similar trend, its error for insulators is about half that of HC, indicating that it can predict electron density with overwhelmingly higher accuracy.

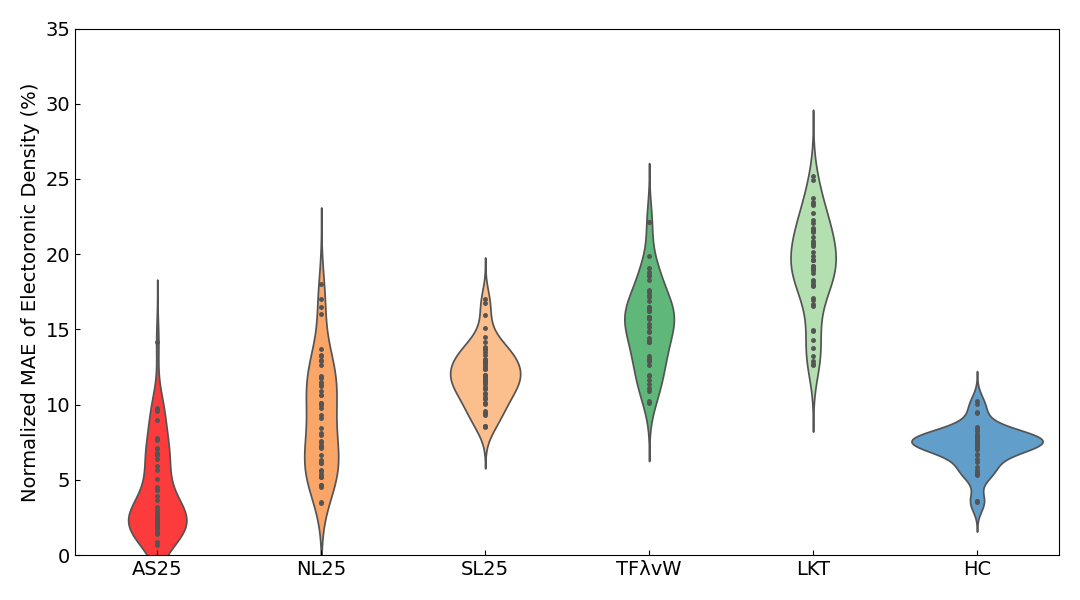
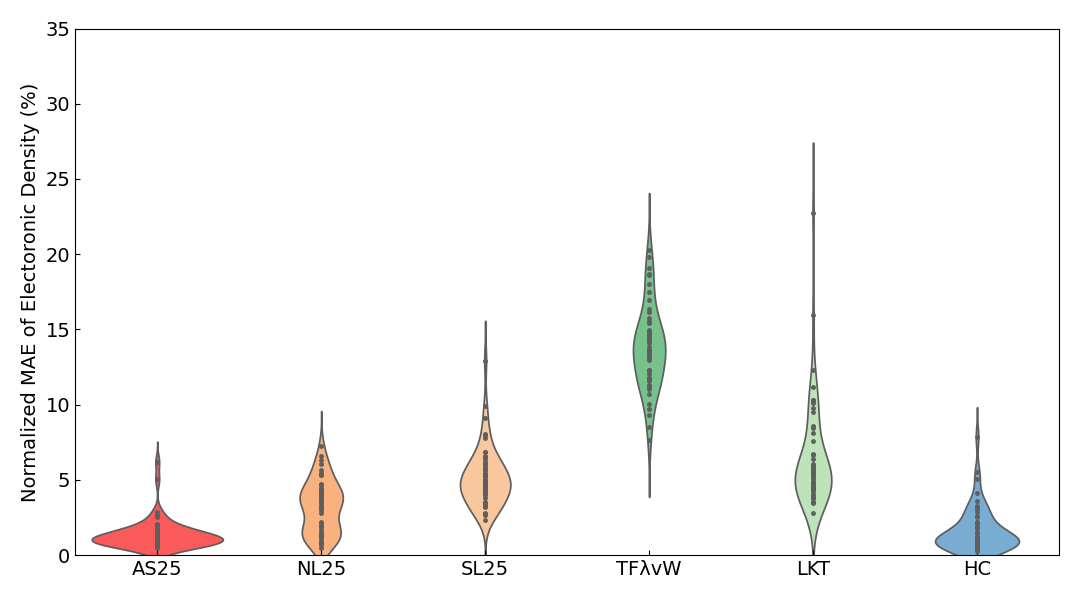
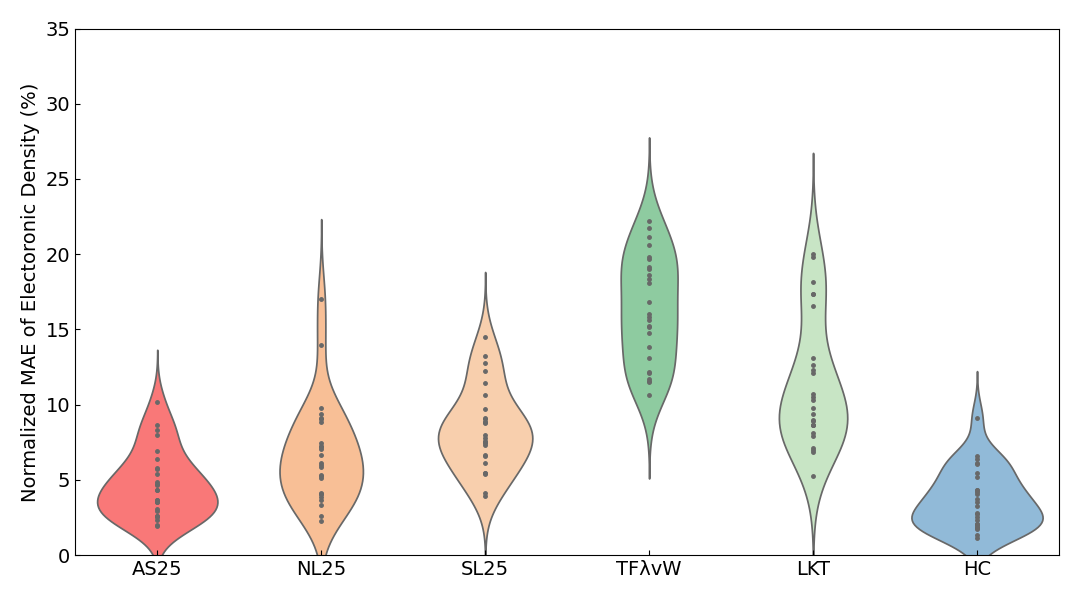
Violin plots⁶ of the Normalized MAE of the electron density are also shown below.


insulator	metal	slab

total

In the violin plots for insulators, metals, and all systems combined, the results for AS25 are distributed in the region with the smallest error. For the slab results, although the average error of AS25 is slightly inferior to HC, the violin plots show that the distribution of errors is almost identical.

Prediction Accuracy of Total Energy#

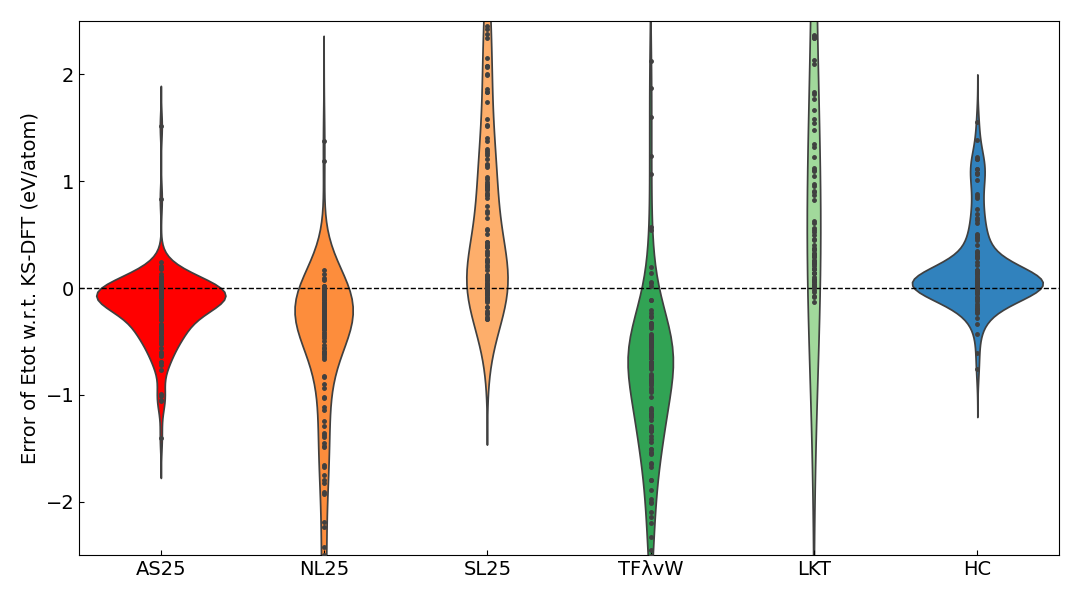
The MAE for the total energy per atom with respect to the KS-DFT results was calculated and is shown in the table below. A violin plot of the error relative to the KS-DFT results is also shown.

MAE of E_tot (eV/atom)
AS25	2.47×10^-1
NL25	6.69×10^-1
SL25	8.26×10^-1
TFλvW	1.02
LKT	2.89
HC	2.56×10^-1

The table and violin plot show that AS25 has the smallest MAE, and its error distribution is most concentrated around the range of -0.1 to 0.1 eV/atom.

Prediction Accuracy of Formation Energy#

The energy per atom, $E_i$ , for the standard state of each of the 27 elements was calculated. Then, for each structure in the test data, the formation energy was calculated using the following formula:

$E_{\mathrm{f}} = \frac{1}{\sum_i n_i } \left( E_{\mathrm{total}} - \sum_i n_i E_i \right)$

Here, $E_{\mathrm{total}}$ and $n_i$ are the total energy of the target structure and the number of atoms of element $i$ contained within it, respectively.

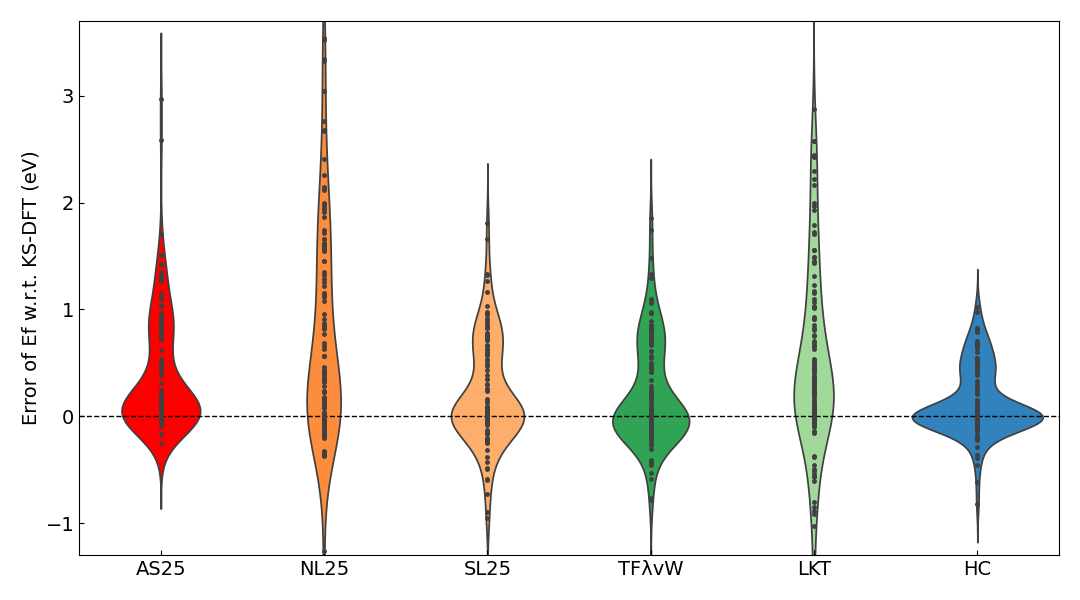
The MAE of the formation energy calculated with each KE functional with respect to the KS-DFT results is shown in the table below. A violin plot of the error relative to the KS-DFT results is also shown.

MAE of E_f (eV)
AS25	3.99×10^-1
NL25	8.69×10^-1
SL25	3.69×10^-1
TFλvW	3.59×10^-1
LKT	7.09×10^-1
HC	2.18×10^-1

The MAE of the formation energy for AS25 is on the same order of magnitude as the MAE of the total energy. The distribution in the violin plot is similarly most concentrated around -0.1 to 0.1 eV/atom, as was the case for the total energy. The apparent improvement in error for formation energy compared to total energy for other KE functionals is likely due to the cancellation of systematic errors when calculating a relative value instead of an absolute one.

Prediction Accuracy of Surface Energy#

The total energy of the bulk structure, $E_{\text{bulk}}$ , corresponding to the 26 slab structures in the test data was also calculated to determine the surface energy using the following formula:

$E_{\text{surf}} = \frac{E_{\text{slab}} - E_{\text{bulk}}}{2A}$

Here, $E_{\text{slab}}$ and $A$ are the total energy and surface area of the slab structure, respectively.

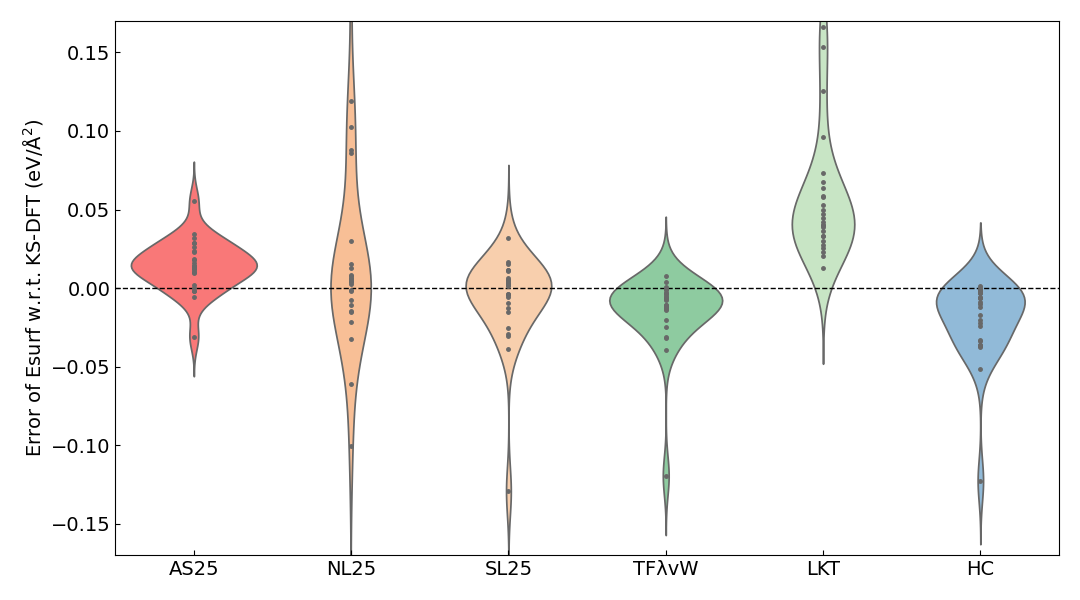
The MAE of the surface energy calculated with each KE functional with respect to the KS-DFT results is shown in the table below. A violin plot of the error relative to the KS-DFT results is also shown.

MAE of E_surf (eV/Å²)
AS25	1.75×10^-2
NL25	3.76×10^-2
SL25	1.67×10^-2
TFλvW	1.58×10^-2
LKT	5.62×10^-2
HC	2.06×10^-2

The MAE of the surface energy for AS25 is on the order of 1×10^-2 eV/Å², and the error distribution is most concentrated around 0 to 0.03 eV/Å².

Conclusion and Outlook#

The calculation results of this study show that the accuracy of the deep learning kinetic energy functional AdvanceSoft25 (AS25) is comprehensively superior to all conventional KE functionals for electron density distribution calculations. For various energy metrics, it possesses accuracy that is comparable to or greater than that of conventional KE functionals.

Furthermore, the high accuracy achieved on the test data, which was separated from the training data, demonstrates that AS25 can be used universally for any combination of elemental species for which pseudopotentials are available. It was also shown that AS25 can be sufficiently applied to insulators, which was considered a weak point for conventional KE functionals.

In the future, further accuracy improvements can be expected through measures such as expanding the training data, increasing the number of deep layers, and improving the electron density optimization algorithm. Additionally, updates are planned to expand the corresponding pseudopotentials to all elements, enabling even more versatile use.