深層学習運動エネルギー汎関数AdvanceSoft25によるK/Mg(0001)吸着系の仕事関数の計算#

材料物性予測のための密度汎関数理論(DFT)計算の解法として最も広く知られているKohn-Sham DFT (KS-DFT)では、計算コストが系のサイズに対して $O(N^3)$ で増大することが課題でした。これを解決する手法として提案されたOrbital-Free DFT (OF-DFT)では、計算コストが $O(N)$ でスケールし、大きなサイズの系に対しても高速な計算を実現します。

一方で、OF-DFTでは実用に耐えうる精度の運動エネルギー汎関数が未知であることが課題でした。そこで、アドバンスソフト株式会社では、独自の場の深層化アルゴリズムを適用した深層学習運動エネルギー汎関数AdvanceSoft25 (AS25)を開発し、Advance/OF-DFTに搭載しました。 AS25は、OF-DFTの最大のメリットである $O(N)$ の計算コストを維持しながら、従来の運動エネルギー汎関数よりも高精度な電子密度計算を実現しました。

また、OF-DFTは、KS-DFTの代替として研究されている $O(N)$ の計算手法の一つであるグラフニューラルネットワーク力場とは異なり、電子やホールのドープを伴う計算も可能です。この特長を利用して、電子数 $N$ によるエネルギーの微分であるフェルミエネルギー $E_\mathrm{F}=dE/dN$ を算出し、真空準位 $E_\mathrm{vac}$ との差分から仕事関数を求めるなどの応用的な計算が可能です。

本記事では、AS25の応用事例として、MgスラブへのK原子の吸着による仕事関数の変化を計算しました。

計算条件#

計算対象とする構造として、Materials Projectより取得したhcpのMgの構造ファイル (mp-153) をもとに、面方位(0001)・原子層三層の2×2スラブモデルを作成しました。このとき、真空層の厚さは26.7Åとしました。また、このスラブモデルの上下の表面のtopサイトにK原子を吸着させたモデルも作成しました¹。

以下の条件で各構造に対してKS-DFT及びOF-DFTを実行しました。

KS-DFTの計算条件

波動関数のカットオフエネルギー : 810 eV
エネルギーの収束閾値 : ~ 1.4×10^-5 eV
擬ポテンシャル : OEPP
交換相関汎関数 : LDA
k点サンプリング : 0.05 Å^-1

OF-DFTの計算条件

波動関数のカットオフエネルギー : 810 eV
エネルギーの収束閾値 : 1.0×10^-3 eV
擬ポテンシャル : OEPP
交換相関汎関数 : LDA
プレコンディショナー : damping関数 ²

KS-DFTにはQuantum ESPRESSO 6.7 (アドバンスソフト改修版)を使用しました。 OF-DFTの運動エネルギー汎関数（KE汎関数）としては、AS25に加えて、既存のよく知られているTFλvW、LKT、HC³を用いて計算を行いました。

また、プレコンディショナーのカットオフ半径は、AS25に対しては0.26 Å、それ以外の従来KE汎関数に対してはその半分の0.13 Åとして計算を行いました⁴。

本事例では、LKTを用いて上記の条件で収束させた電子密度を、他のKE汎関数を用いたOF-DFT計算の初期電子密度として使用しています。これによって、電子密度が局所解に収束することを防いでいます。


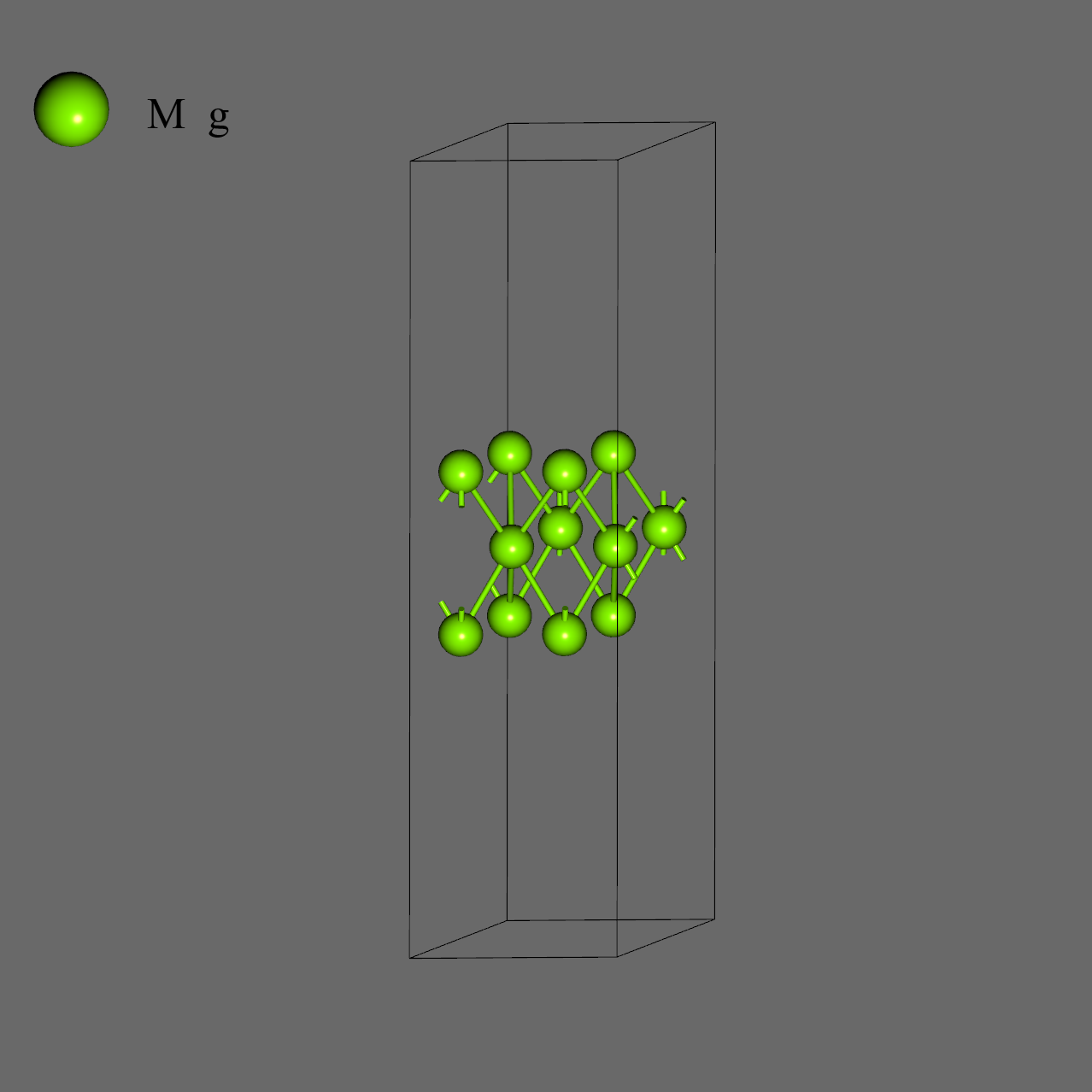
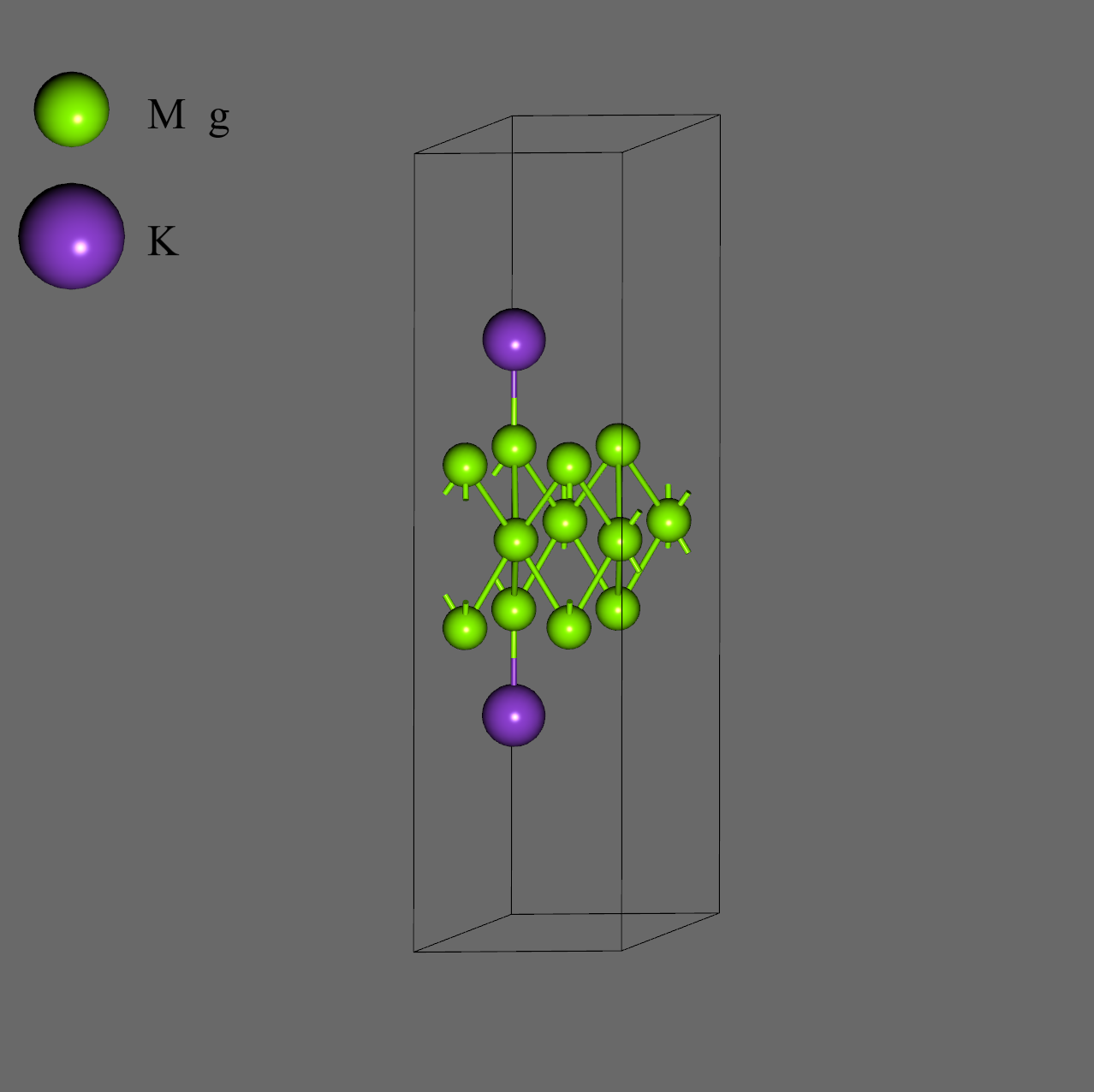
Mg (0001)	K / Mg (0001)

計算結果#

中性の各スラブに対するKS-DFTおよびOF-DFTの結果から、位置zの面内の静電ポテンシャルの平均を算出し、以下にプロットしました。スラブから十分に離れた周期境界付近におけるポテンシャルの値が真空準位 $E_\mathrm{vac}$ に対応します。


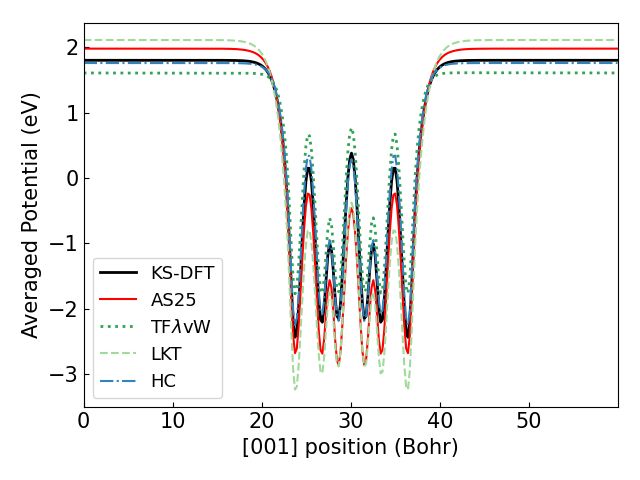
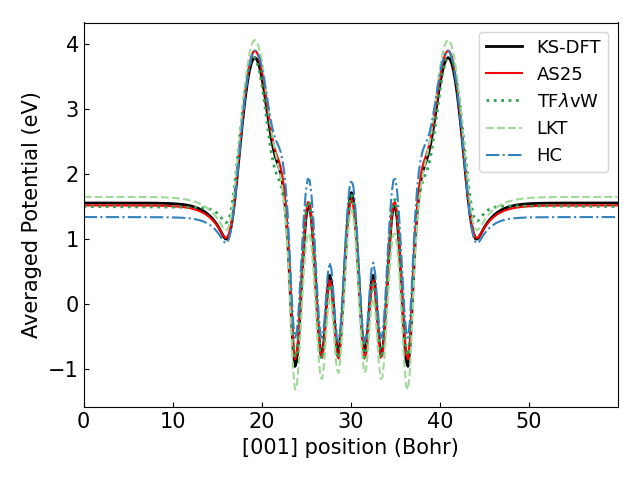
Mg (0001) の平均ポテンシャル	K / Mg (0001)の平均ポテンシャル

上図からは、AS25は特に吸着系におけるポテンシャルを精度よく計算できていることがわかります。

次に、各スラブに電荷 $ΔN=±0.1e$ を付与した各状態について電子密度計算を行い、トータルエネルギー $E$ $(ΔN)$ を求めました。各トータルエネルギーを用いて数値微分 $E_\mathrm{F}=dE/dN$ からフェルミエネルギーを算出し、真空準位との差分である仕事関数 $\mathit{\Phi}=E_\mathrm{F}-E_\mathrm{vac}$ を求めました。

以上の結果を以下の表に示します。

	$E_\mathrm{F}\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$V_\mathrm{vac}\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$\mathit{\Phi}\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$E_\mathrm{F}\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$	$V_\mathrm{vac}\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$	$\mathit{\Phi}\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$
KS	-1.960	1.802	3.762	-0.556	1.555	2.111
AS25	-1.823	1.981	3.804	-0.540	1.518	2.058
TFλvW	-1.628	1.608	3.236	-0.728	1.501	2.228
LKT	-2.560	2.113	4.673	-0.774	1.650	2.424
HC	-1.893	1.760	3.653	-0.238	1.339	1.577

仕事関数の値は、Mg(0001)およびK / Mg (0001)のいずれにおいてもAS25の結果が最もKS-DFTの結果に近く、誤差は各構造でそれぞれ0.042 eV、-0.053 eVとなっています。

また、吸着による仕事関数の変化である $\Delta \mathit{\Phi}=\mathit{\Phi}_\mathrm{K/Mg}-\mathit{\Phi}_\mathrm{Mg}$ と、その値のKS-DFTに対する絶対誤差(Absolute Error(AE))を算出し、以下の表及び図に示します。

	$\Delta \mathit{\Phi}$ $\mathrm{[eV]}$	$\mathrm{AE}$ $\mathrm{of}$ $\Delta \mathit{\Phi}$ $\mathrm{[eV]}$
KS	-1.650	-
AS25	-1.746	0.096
TFλvW	-1.008	0.642
LKT	-2.249	0.599
HC	-2.076	0.426

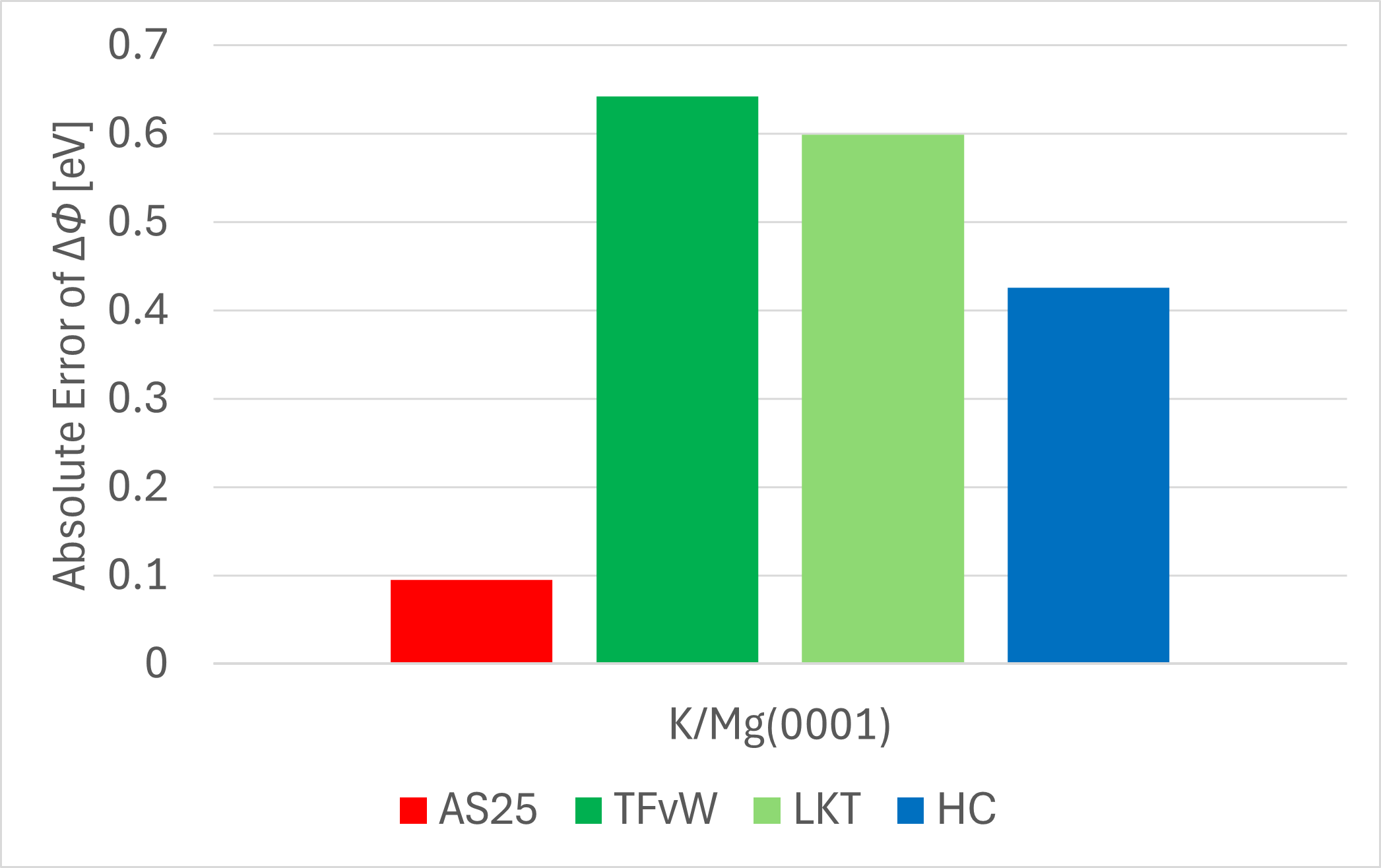
AS25は、KS-DFTの結果に対する誤差が0.1 eV以下であり、いずれの従来KE汎関数よりも高い精度で吸着による仕事関数の変化を予測できていることがわかります。

なお、先行研究⁵のKS-DFT計算によるK/Mg(0001) (topサイト)の $\Delta \mathit{\Phi}$ は-1.53 eVであり、原子層数や擬ポテンシャルなどの計算条件の詳細が異なることを考慮すると、本事例の計算結果は妥当なものであるといえます。

総括と展望#

本事例の結果から、AS25は、単純なスラブだけではなく吸着系においても高精度に仕事関数を計算できることがわかりました。 AS25の教師データには吸着系は含まれていないため、この結果はAS25の高い汎用性を示唆しています。吸着種や吸着位置を変えながら計算を行うことで、仕事関数の変調を目的とした材料設計も可能であると考えられます。さらに、Effective Screening Medium (ESM)法を実装すれば、上下非対称なスラブについても仕事関数の計算を容易に実行できるようになります。

以上のように、AS25は、KS-DFTよりも低コストなOF-DFTにおいて、応用的な計算を実用に耐えうる精度で実行可能にします。

深層学習運動エネルギー汎関数AdvanceSoft25によるK/Mg(0001)吸着系の仕事関数の計算#

計算条件#

計算結果#

総括と展望#

関連ページ#