Work Function Calculation of a K/Mg(0001) Adsorption System Using the Deep Learning Kinetic Energy Functional AdvanceSoft25

Kohn-Sham DFT (KS-DFT), the most widely known method for Density Functional Theory (DFT) calculations for material property prediction, has the challenge that its computational cost increases on the order of $O(N^3)$ with respect to the system size. Orbital-Free DFT (OF-DFT) was proposed as a method to solve this issue. In OF-DFT, the computational cost scales as $O(N)$, enabling high-speed calculations even for large systems.

On the other hand, a major challenge for OF-DFT has been the lack of a known kinetic energy functional with sufficient accuracy for practical use. Therefore, AdvanceSoft Corporation has developed the deep learning kinetic energy functional AdvanceSoft25 (AS25), which applies a proprietary "field-deepening" algorithm, and has integrated it into Advance/OF-DFT. While maintaining the $O(N)$ computational cost, the primary advantage of OF-DFT, AS25 achieves more accurate electron density calculations than conventional kinetic energy functionals.

Furthermore, unlike graph neural network force fields, which are another $O(N)$ computational method being researched as an alternative to KS-DFT, OF-DFT can also perform calculations involving electron or hole doping. This feature allows for advanced calculations, such as determining the Fermi energy $E_\mathrm{F}=dE/dN$ by taking the derivative of the energy with respect to the number of electrons $N$, and then calculating the work function from the difference with the vacuum level $E_\mathrm{vac}$.

In this article, as an application case of AS25, we calculated the change in the work function of a Mg slab due to the adsorption of K atoms.

Calculation Conditions

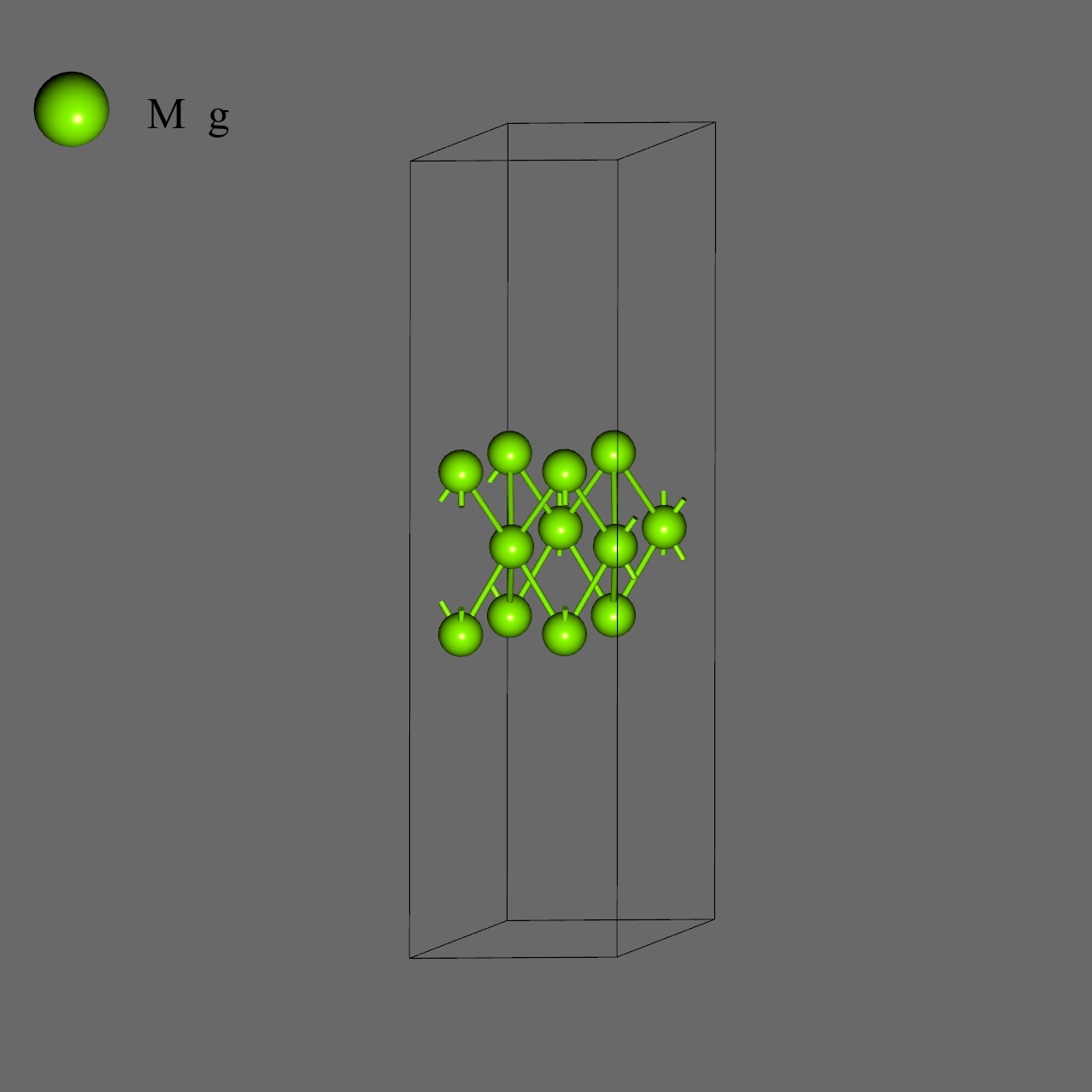
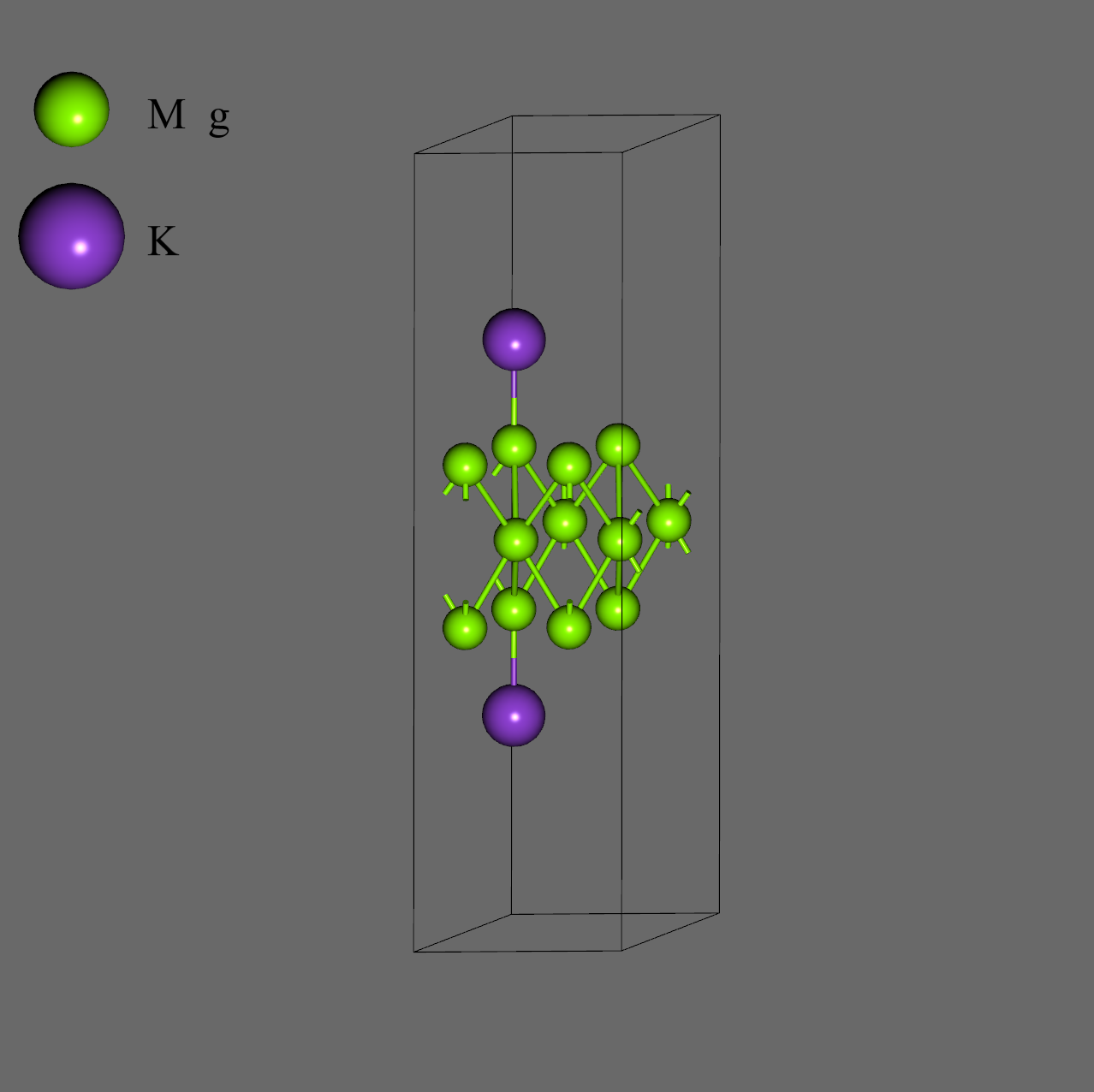
As the calculation target, we created a 2x2 slab model of the (0001) surface with three atomic layers, based on an hcp Mg structure file (mp-153) obtained from the Materials Project. The thickness of the vacuum layer was set to 26.7 Å. We also created a model where K atoms were adsorbed on the 'top' sites of both the upper and lower surfaces of this slab model¹.

We performed KS-DFT and OF-DFT calculations for each structure under the following conditions.

KS-DFT Calculation Conditions

• Wave function cutoff energy: 810 eV
• Energy convergence threshold: ~ 1.4×10^-5 eV
• Pseudopotential: OEPP
• Exchange-correlation functional: LDA
• k-point sampling: 0.05 Å^-1

OF-DFT Calculation Conditions

• Wave function cutoff energy: 810 eV
• Energy convergence threshold: 1.0×10^-3 eV
• Pseudopotential: OEPP
• Exchange-correlation functional: LDA
• Preconditioner: damping function ²

We used Quantum ESPRESSO 6.7 (AdvanceSoft modified version) for the KS-DFT calculations. For the OF-DFT kinetic energy functional (KE functional), in addition to AS25, we performed calculations using the existing well-known functionals TFλvW, LKT, and HC³.

The cutoff radius for the preconditioner was set to 0.26 Å for AS25, and half of that, 0.13 Å, for the other conventional KE functionals⁴.

In this study, the electron density converged using LKT under the above conditions was used as the initial electron density for the OF-DFT calculations with the other KE functionals. This helps to prevent the electron density from converging to a local minimum.

Mg (0001)	K / Mg (0001)

Calculation Results

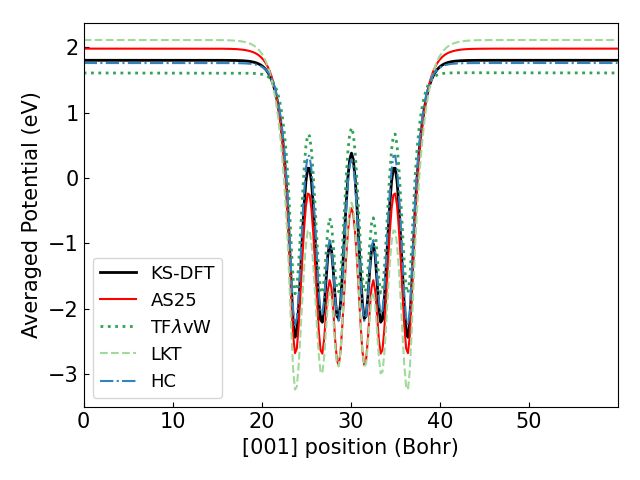
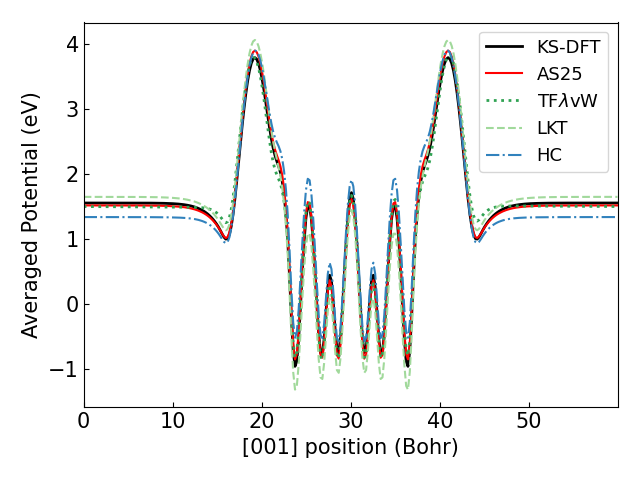
From the KS-DFT and OF-DFT results for each neutral slab, we calculated the in-plane average of the electrostatic potential as a function of position z and plotted it below. The value of the potential near the periodic boundary, sufficiently far from the slab, corresponds to the vacuum level $E_\mathrm{vac}$.

Average potential of Mg (0001)	Average potential of K / Mg (0001)

The figure above shows that AS25 can calculate the potential with high accuracy, particularly for the adsorption system.

Next, we performed electron density calculations for each state of the slabs with an added charge of $\Delta N = \pm 0.1e$ to obtain the total energy $E(\Delta N)$. Using these total energies, we calculated the Fermi energy via numerical differentiation, $E_\mathrm{F}=dE/dN$, and then determined the work function, $\Phi=E_\mathrm{vac}-E_\mathrm{F}$, which is the difference from the vacuum level.

The results are summarized in the table below.

	$E_\mathrm{F}\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$E_\mathrm{vac}\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$\Phi\ \mathrm{(Mg)}$ $\mathrm{[eV]}$	$E_\mathrm{F}\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$	$E_\mathrm{vac}\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$	$\Phi\ \mathrm{(K/Mg)}$ $\mathrm{[eV]}$
KS	-1.960	1.802	3.762	-0.556	1.555	2.111
AS25	-1.823	1.981	3.804	-0.540	1.518	2.058
TFλvW	-1.628	1.608	3.236	-0.728	1.501	2.228
LKT	-2.560	2.113	4.673	-0.774	1.650	2.424
HC	-1.893	1.760	3.653	-0.238	1.339	1.577

The work function values from AS25 are the closest to the KS-DFT results for both Mg(0001) and K/Mg(0001), with errors of 0.042 eV and -0.053 eV for each structure, respectively.

Next, we calculated the change in work function due to adsorption, $\Delta \Phi=\Phi_\mathrm{K/Mg}-\Phi_\mathrm{Mg}$, and its absolute error (AE) with respect to the KS-DFT value. The results are shown in the table and figure below.

	$\Delta \Phi$ $\mathrm{[eV]}$	$\mathrm{AE}$ $\mathrm{of}$ $\Delta \Phi$ $\mathrm{[eV]}$
KS	-1.650	-
AS25	-1.746	0.096
TFλvW	-1.008	0.642
LKT	-2.249	0.599
HC	-2.076	0.426

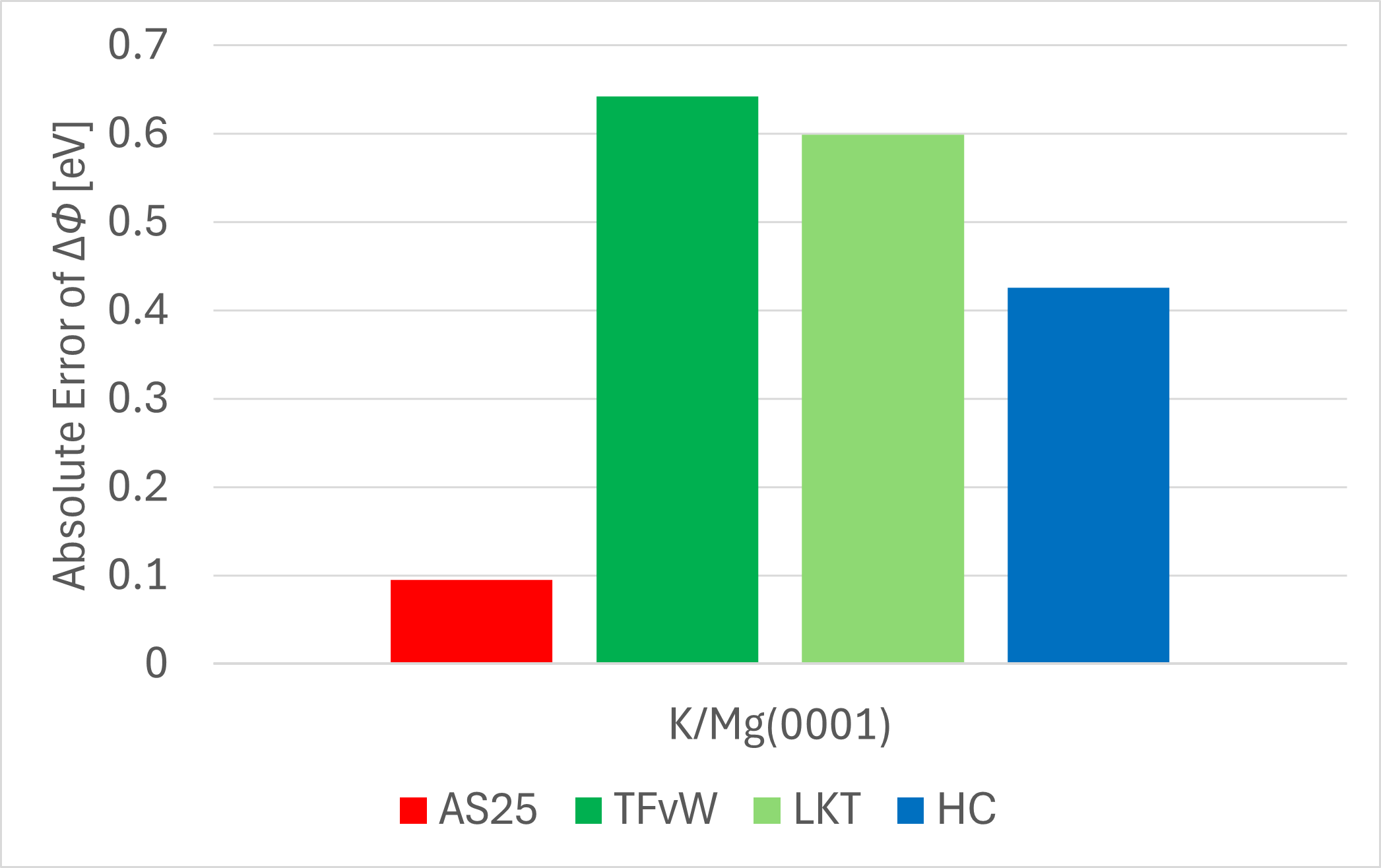
AS25 predicts the change in work function due to adsorption with an error of less than 0.1 eV relative to the KS-DFT result, which is significantly more accurate than any of the conventional KE functionals.

For reference, the $\Delta \Phi$ for K/Mg(0001) (top site) from a previous KS-DFT study⁵ was -1.53 eV. Considering the differences in calculation details such as the number of atomic layers and the pseudopotential, the results of this study can be considered reasonable.

Conclusion and Outlook

The results of this study show that AS25 can accurately calculate the work function not only for simple slabs but also for adsorption systems. This result suggests the high versatility of AS25, as its training data did not include adsorption systems. It is conceivable that materials design for work function modulation could be performed by carrying out calculations while varying the adsorbate species and adsorption sites. Furthermore, implementing the Effective Screening Medium (ESM) method would make it easier to perform work function calculations for asymmetrically adsorbed slabs.

As demonstrated, AS25 enables advanced calculations in OF-DFT, which is less costly than KS-DFT, with an accuracy sufficient for practical applications.

関連ページ

• 深層学習Orbital-Free DFTソフトウェア Advance/OF-DFT
• 解析分野：ナノ・バイオ
• 産業分野：材料・化学
• Advance/OF-DFT Product Information
• Advance/OF-DFT Product Introduction Seminar

---

1. K atoms are adsorbed symmetrically on both sides to prevent the formation of a dipole and a resulting slope in the potential. ↩

2. The preconditioner is an operator implemented by our company to suppress the high-frequency noise known to be present in the functional derivative of machine learning kinetic energy functionals. ↩

3. The parameters for TFλvW were λ=0.2, for LKT a=1.3, and for HC β=2/3, λ=0.0. ↩

4. For conventional KE functionals, if high-frequency components are cut too aggressively, the electron density tends to oscillate near the solution during energy minimization. To prevent this, the cutoff radius is set to a slightly smaller value. ↩

5. Kiejna, A., Ossowski, T., & Wachowicz, E. (2004). Alkali metals adsorption on the Mg (0001) surface. Surface science, 548(1-3), 22-28. ↩