コンテンツにスキップ

深層学習運動エネルギー汎関数AdvanceSoft25と先行研究の機械学習運動エネルギー汎関数の性能比較#

材料物性予測のための密度汎関数理論(DFT)計算の解法として最も広く知られているKohn-Sham DFT (KS-DFT)では、計算コストが系のサイズに対してで増大することが課題でした。これを解決する手法として提案されたOrbital-Free DFT (OF-DFT)では、計算コストがでスケールし、大きなサイズの系に対しても極めて高速な計算を実現します。

一方で、OF-DFTでは計算精度を大きく左右する運動エネルギー汎関数として十分な精度を持つものが未知であることが課題でした。 そのような状況のなかで、運動エネルギーの精度を向上する手段として機械学習による運動エネルギー汎関数の開発も進められてきました。

2025年8月時点で発表されている最も優れた機械学習運動エネルギー汎関数の一つとして、Chenら1により報告された、非局所特徴ベクトルを用いた機械学習運動エネルギー汎関数CPN5が挙げられます。 CPN5は、電子密度の勾配及びラプラシアンに非局所カーネルをかけて積分したものを特徴ベクトルに追加することで、従来の準局所特徴ベクトルを用いた機械学習運動エネルギー汎関数と比較して高精度な計算を実現しましたが、精度や汎用性は実用化レベルには達していませんでした。

そこで、アドバンスソフト株式会社では、独自の場の深層化アルゴリズムを適用した深層学習運動エネルギー汎関数AdvanceSoft25 (AS25)を開発し、Advance/OF-DFTに搭載しました。 AS25は、グラフ理論を連続多変数空間に拡張して「場」に対して適用することで深層学習を可能にし、従来の機械学習運動エネルギー汎関数よりも高い精度・優れた汎用性を実現しました。

本事例では、深層学習運動エネルギー汎関数AdvanceSoft25と先行研究の機械学習運動エネルギー汎関数CPN5の性能比較を実施しました。

計算条件#

対象とする構造は、六方晶の半導体であるSi, AlP, AlAs, AlSb, GaP, GaAs, GaSb, InP, InAs, InSbの10構造です。本事例では、Materials Projectより取得した構造ファイルを用いて計算を行いました。

以下の条件で各構造に対してKS-DFT及びOF-DFTを実行し、基底状態における電子密度分布を求めました。

本事例 先行研究1
波動関数のカットオフエネルギー(KS-DFT) 1350 eV 800 eV
波動関数のカットオフエネルギー(OF-DFT) 1350 eV 3200 eV
エネルギーの収束閾値 1×10-4 eV 記載なし
擬ポテンシャル OEPP BLPS
交換相関汎関数 LDA PBE
k点サンプリング (KS-DFT) 0.05 Å-1 ~ 0.09 Å-1
プレコンディショナー (OF-DFT) 有り 2 無し
構造最適化 無し 有り

KS-DFTにはQuantum ESPRESSO 6.7 (アドバンスソフト改修版)を使用しました。OF-DFTの運動エネルギー汎関数（KE汎関数）としては、AS25と既存のよく知られているTFλvW、LKT、HC3に加えて、比較用にAS25のアーキテクチャから場の深層化を取り除いて学習した非局所モデルのNL25、準局所モデルのSL25を用いて計算を行いました。

計算結果#

電子密度分布の予測精度#

以下の式で定義される、KS-DFTの結果に対する電子密度の平均絶対相対誤差 (Mean Absolute Relative Error (MARE))を、KE汎関数ごとの結果について算出し、以下の棒グラフに示します。また、CPN5のMAREの文献値1も併せてプロットしています。

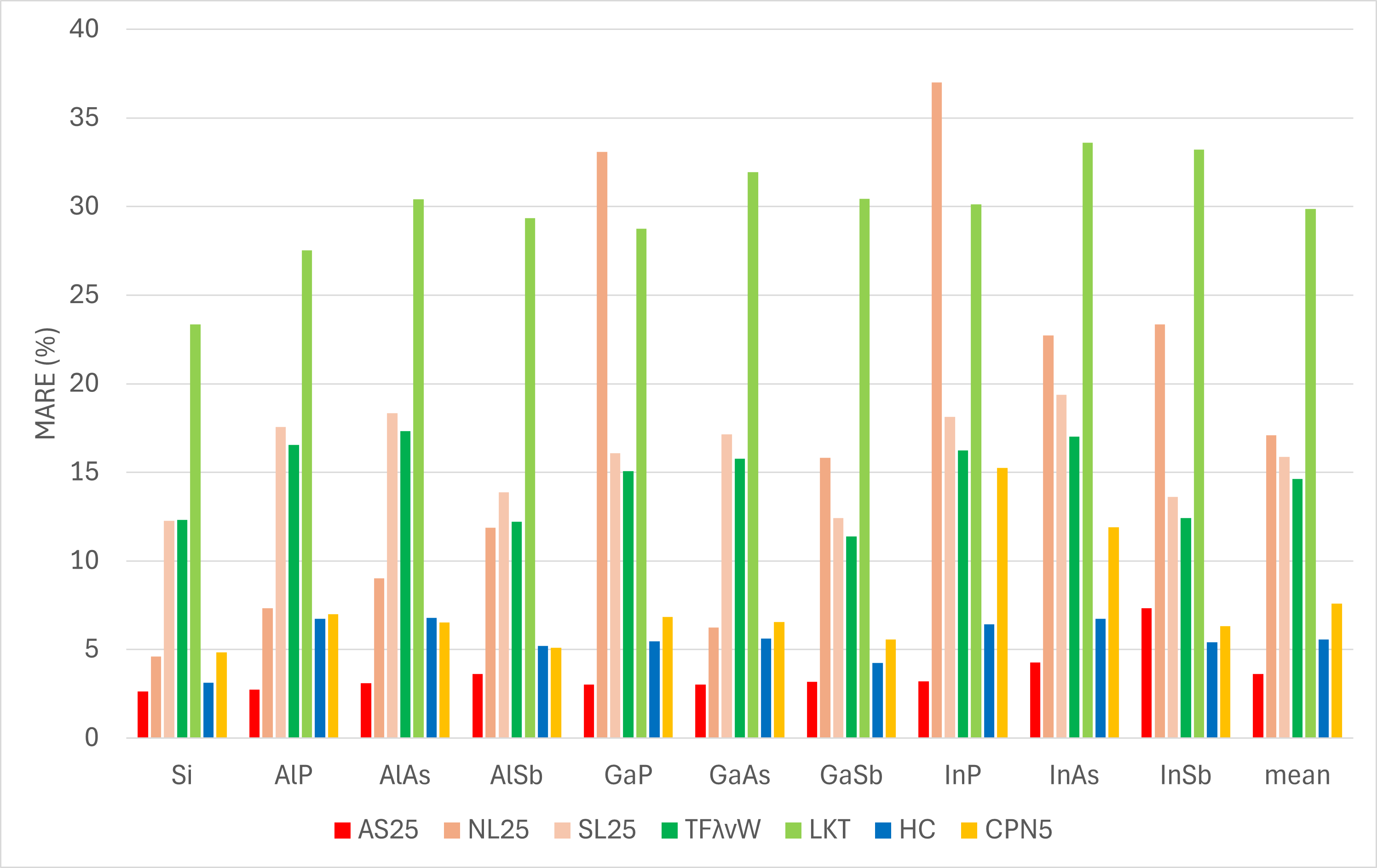
上図では、InSb以外の全ての構造において、AS25は他のいずれの汎関数よりもMAREが小さくなっており、高精度な電子密度分布予測を実現できていることがわかります。また、InSbにおいても、HCやCPN5とのMAREの差は数%程度にとどまっています。10構造のMAREの平均は、AS25では 3.61 %となっており、CPN5の 7.59 %の半分以下にまで小さくなっています。

また、CPN5は10個の六方晶半導体に対応する10個の立方晶半導体についてのみ学習しているのに対して、それとは無関係に合計約4000点の教師データ4について学習しているAS25の方が高い精度での電子密度計算を実現しており、AS25が圧倒的に優れた汎用性を持つことがわかります。

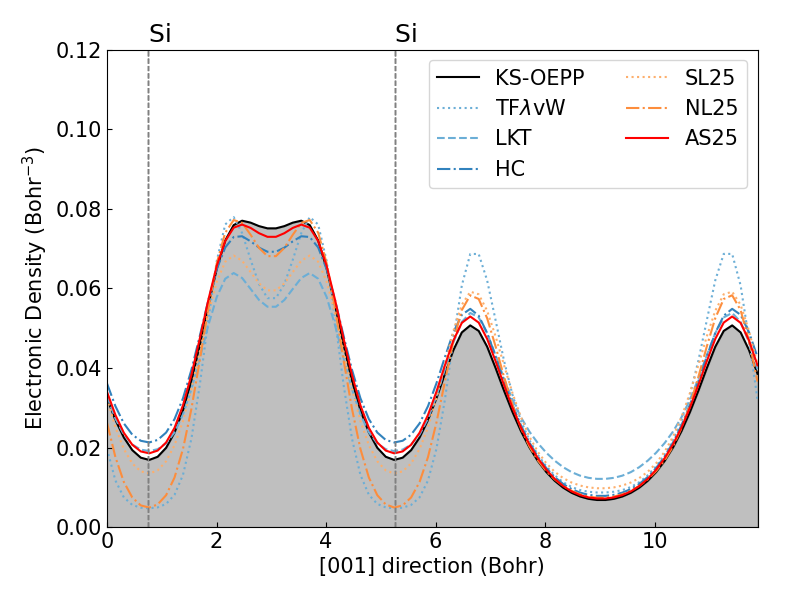
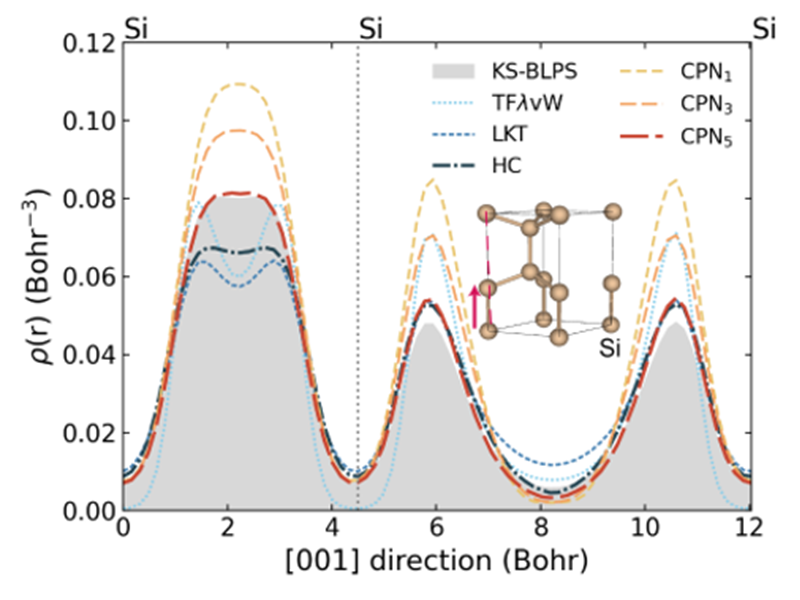
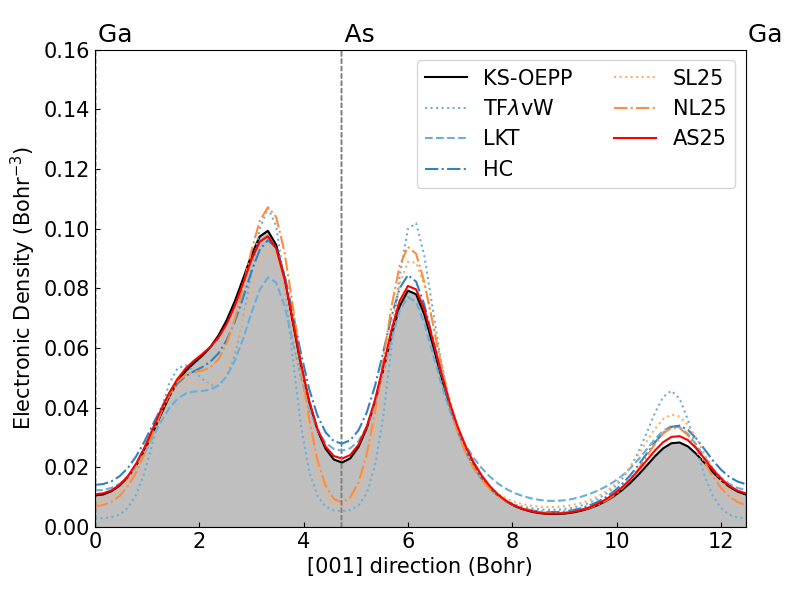
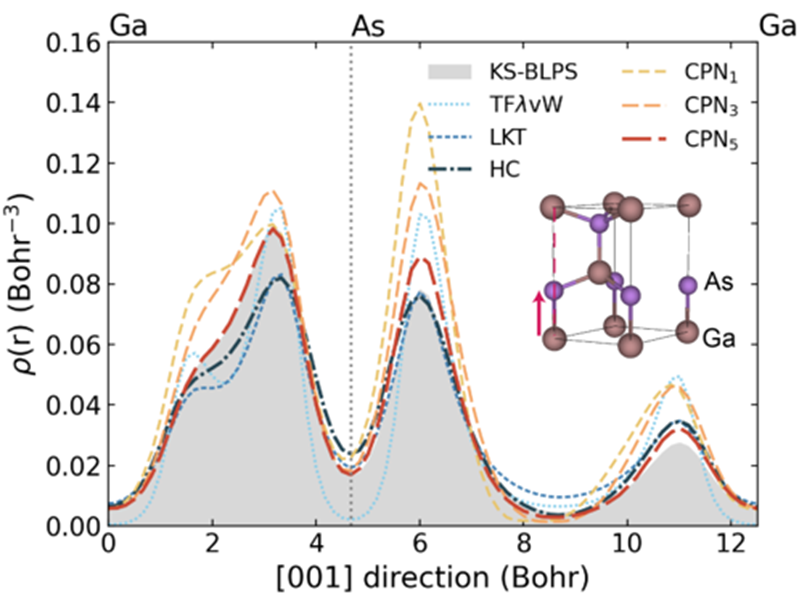
また、以下には、SiとGaAsにおける電子密度のプロットを示します。左の列がAdvance/OF-DFTによる計算結果、右の列がChenらによる計算結果1を引用したものとなっています。横軸は、c軸に平行で原子中心を通る直線上の位置座標に対応し、縦軸は電子密度の値に対応しています。

Siの電子密度分布 (本事例) Siの電子密度分布 (先行研究1)
GaAsの電子密度分布 (本事例) GaAsの電子密度分布 (先行研究1)

Si, GaAsのいずれのプロットにおいても、黒線で示されているKS-DFTの結果と赤線で示されているAS25の結果がほとんど一致しており、CPN5と比較してより高精度にKS-DFTの結果を再現していることがわかります。 なお、左右の図でKS-DFTの結果の電子密度分布がやや異なるのは、主に擬ポテンシャルと交換相関汎関数が異なることに由来します。

総括と展望#

本事例の結果から、深層学習運動エネルギー汎関数 AdvanceSoft25 (AS25)は、現行の最も優れた機械学習運動エネルギー汎関数の一つであるCPN5よりも、圧倒的に優れた精度と汎用性を持つことがわかりました。

AS25を用いることで、KS-DFTよりも低い計算コストかつ従来のOF-DFTよりも高精度に、材料開発のための物性計算を行うことが可能となります。

今後は、教師データやモデルのアーキテクチャ、収束アルゴリズムの改善により更なる精度向上を行う予定です。また、対応する擬ポテンシャルを全元素へと拡充し、より汎用的に使用できるように研究開発を進めています。

関連ページ#

  1. Sun, L., & Chen, M. (2024). Multi-channel machine learning based nonlocal kinetic energy density functional for semiconductors. Electronic Structure, 6(4), 045006. ↩↩↩↩

  2. プレコンディショナーは、機械学習運動エネルギー汎関数の汎関数微分に含まれることが知られている高周波ノイズを抑えるために弊社で実装した演算子です。本事例ではカットオフ半径を0.25 Åとしたdamping関数を使用しました。 ↩

  3. TFλvWのパラメータはλ=0.2、LKTのパラメータはa=1.3、HCのパラメータはβ=2/3, λ=0.0としました。 ↩

  4. 27元素種・約1000個の結晶構造と、それらに真空層の追加や体積・局所ポテンシャルの変調を施した構造に対するKS-DFTの計算結果を教師データとして使用しました。 ↩