Melting Point Analysis of Nuclear Fuel Materials Using Multiple Neural Network Models#
Click here for the analysis results.
Force Field Representation Using the Mean Value of Multiple Neural Network Models.#
In NeuralMD, a multilayer perceptron that takes symmetric functions representing the chemical environment of each atom as input data is used as a Neural Network force field. This multilayer perceptron outputs energy, but in Ver.1.9, a new feature has been implemented that prepares multiple multilayer perceptrons and expresses energy with their mean value. This method is also adopted in ANI-2x, etc., and it is known that it can be calculated more accurately than using a single multilayer perceptron, even in extrapolation areas where the structure that appears in the process of molecular dynamics calculation is not included in the supervised data. The stability of the Neural Network force field improves, so it is particularly effective for inorganic materials in a molten state or amorphous materials. By combining it with delta-NNP method and Self-Learning Hybrid Monte Carlo method, a stable force field can be easily created even with a relatively small number of supervised data. Figure 1 shows the Neural Network force field in this method.
In addition, applying this method increases the number of variables to be optimized (such as the weights and biases of multilayer perceptrons), so a significant amount of computation time is required to learn the Neural Network force field.
Therefore, Super Epoch method is implemented with the aim of accelerating the learning process.
In Super Epoch method, the supervised data is divided into multiple subsets, and the learning process using L-BFGS method for each subset is performed continuously.
For example, if there are 10,000 supervised data, it is divided into 20 subsets, each containing 500 supervised data.
First, a few hundred epochs of learning are performed using L-BFGS method with the first 500 supervised data.
Then, switch to another 500 supervised data and continue learning.
This is repeated 20 times.
This reduces the amount of computation per epoch, while sharing the symmetric function and its derivative in memory within one subset, thereby avoiding the symmetric function calculation for each epoch.
Furthermore, since only the information of the symmetric functions for 500 structures needs to be stored in memory, a significant reduction in memory usage has also been achieved.
In molecular dynamics calculations, the bottleneck of the computation lies in the symmetric functions and their derivatives, so even if the number of Neural Network models increases, the impact on computation time is negligible.
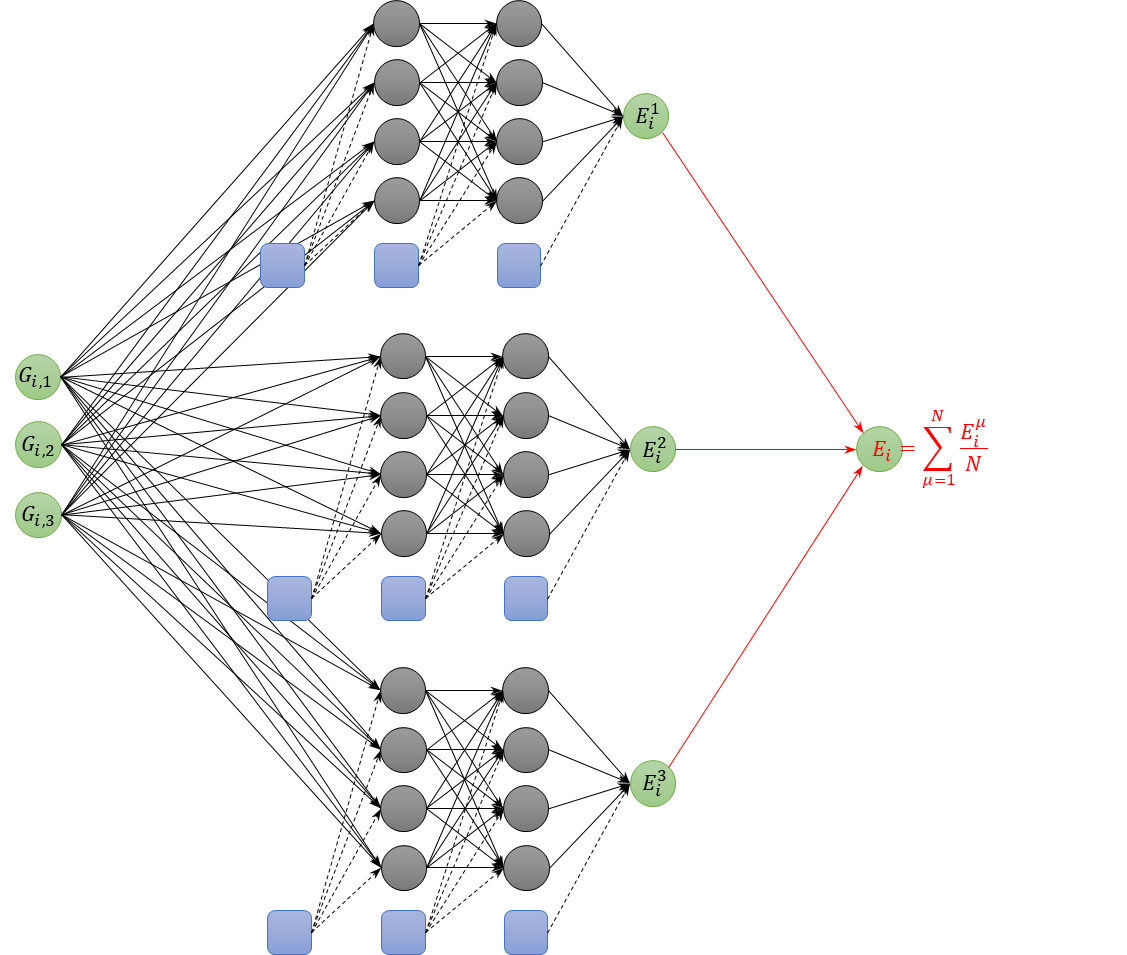 |
|---|
| Figure 1 |
Melting of CeO2/UO2/PuO2#
The method using multiple Neural Network models is suitable for applications such as the melting of inorganic materials. Therefore, in this work, we created Neural Network force fields tailored to the molten states of CeO2, UO2, and PuO2, and conducted an evaluation of their melting points. In creating the Neural Network force fields, we applied Self-Learning Hybrid Monte Carlo method for isothermal-isobaric (NPT) ensemble. The temperature within NPT ensemble was set at 4000K, the pressure at 1.0 bar, and the degrees of freedom for the cell shape were defined as Triclinic. The crystal structure was based on a fluorite-type primitive cell, utilizing a 2 x 2 x 2 supercell (Figure 2). There are a total of 24 atoms. The conditions for the first-principles calculations and Neural Network force field computations are as detailed in Tables 1 and 2 below.
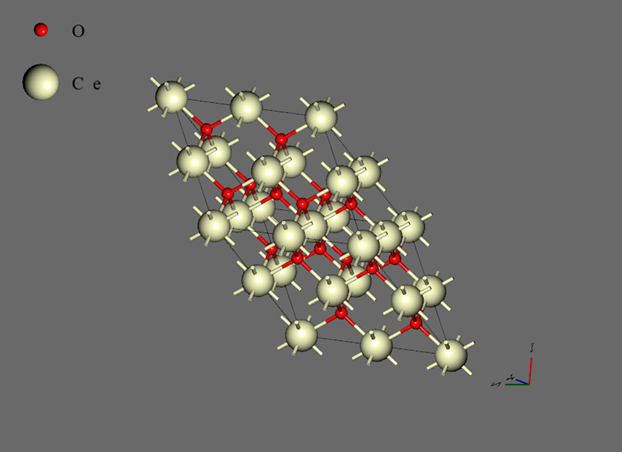 |
|---|
| Figure 2 |
| Conditions for First-Principles Calculations | Settings |
|---|---|
| Pseudopotentials | 【CeO2】Ce.GGA-PBE-paw-v1.0.UPF, o_pbe_v1.2.uspp.F.UPF 【UO2】U.pbe-spfn-rrkjus_psl.1.0.0.UPF, O.pbe-n-rrkjus_psl.1.0.0.UPF 【PuO2】Pu.pbe-spfn-rrkjus_psl.1.0.0.UPF, O.pbe-n-rrkjus_psl.1.0.0.UPF |
| Cutoff Energy | 【CeO2】40Ry, 360Ry 【UO2】47Ry, 420Ry 【PuO2】93Ry, 839Ry |
| k-point Sampling | 2 x 2 x 2 |
| Spin Polarization | None |
| Exchange-Correlation Functional | GGA-PBE |
| Conditions for NN Force Field | Settings |
|---|---|
| delta-NNP method | Applying Lennard-Jones-like Potential |
| Symmetric Functions | Chebyshev Polynomials (Radial Components: 40, 6.0Å, Angular Components: 30, 6.0Å) |
| NN Models | 32 Models x 2 Layers x 35 Nodes |
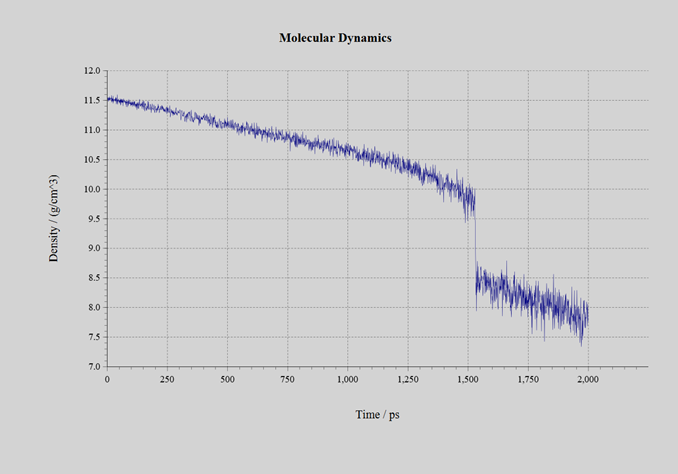
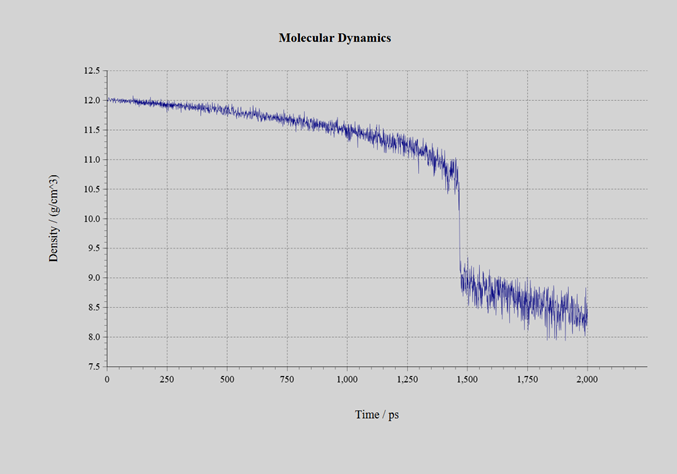
The number of supervised data generated in the process of Self-Learning Hybrid Monte Carlo method is 1634 for CeO2, 650 for UO2, and 1078 for PuO2. Although all were initially in the fluorite-type crystal structure, they melted during the calculation process, and the calculation was continued until they finally evaporated or the cell shape became excessively flat. Molecular dynamics calculations were carried out using the Neural Network force field obtained by Self-Learning Hybrid Monte Carlo method. The RMSE of the created force field is as shown in Table 3. The model used for the calculation is a 3 x 3 x 3 supercell (324-atom system: Figure 3). In the NPT ensemble, a simulation of 2.0ns was carried out with a time step of 1.0fs. The pressure was set at 1.0 bar, and the cell shape was constrained to be Isotropic. The initial temperature was 300K, and the system was linearly heated to 3500K after 2.0ns. During the simulation process, the material melts and changes from solid to liquid. The changes in density are shown in Figures 4, 5, and 6 below. A discontinuous change in density can be observed around 1.4 to 1.6ns. The temperature at this point is the melting point. The melting points of each material are as shown in Table 3 below. Despite the very small number of supervised data, ranging from 600 to 1600, the experimental values of the melting points have been qualitatively reproduced correctly.
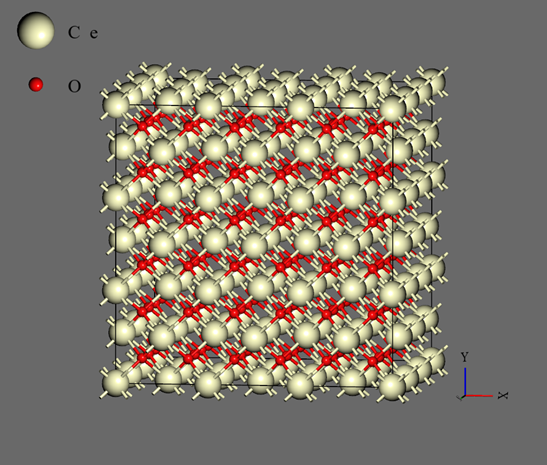 |
|---|
| Figure 3 |
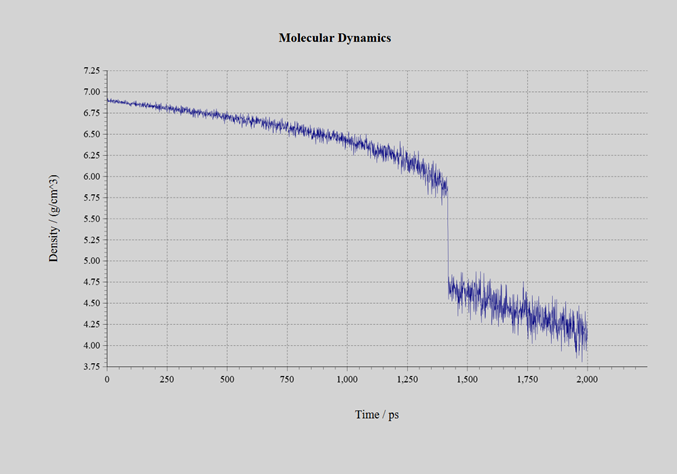
|
|
|
Figure 4:CeO2 |
Figure 5:UO2 |
Figure 6:PuO2 |
| RMSE of Energy | RMSE of Force | Calculated Melting Point | Experimental Melting Point | |
|---|---|---|---|---|
| CeO2 | 0.020 eV/atom | 0.29 eV/A | 2299℃ | Approximately 2400℃ |
| UO2 | 0.018 eV/atom | 0.29 eV/Å | 2476℃ | Approximately 2800℃ |
| PuO2 | 0.018 eV/atom | 0.29 eV/Å | 2376℃ | Approximately 2400℃ |