自己学習ハイブリッドモンテカルロ法による金属触媒上に吸着した水素原子の分子動力学計算#
Pt3Ni金属触媒上に水素原子を吸着させた場合のNeural Network力場(NNP)を自己学習ハイブリッドモンテカルロ(SLHMC)法を用いて作成し、NNPを用いた分子動力学(MD)計算を行って吸着距離などの計算を行った。
SLHMC法を用いたNNP作成#
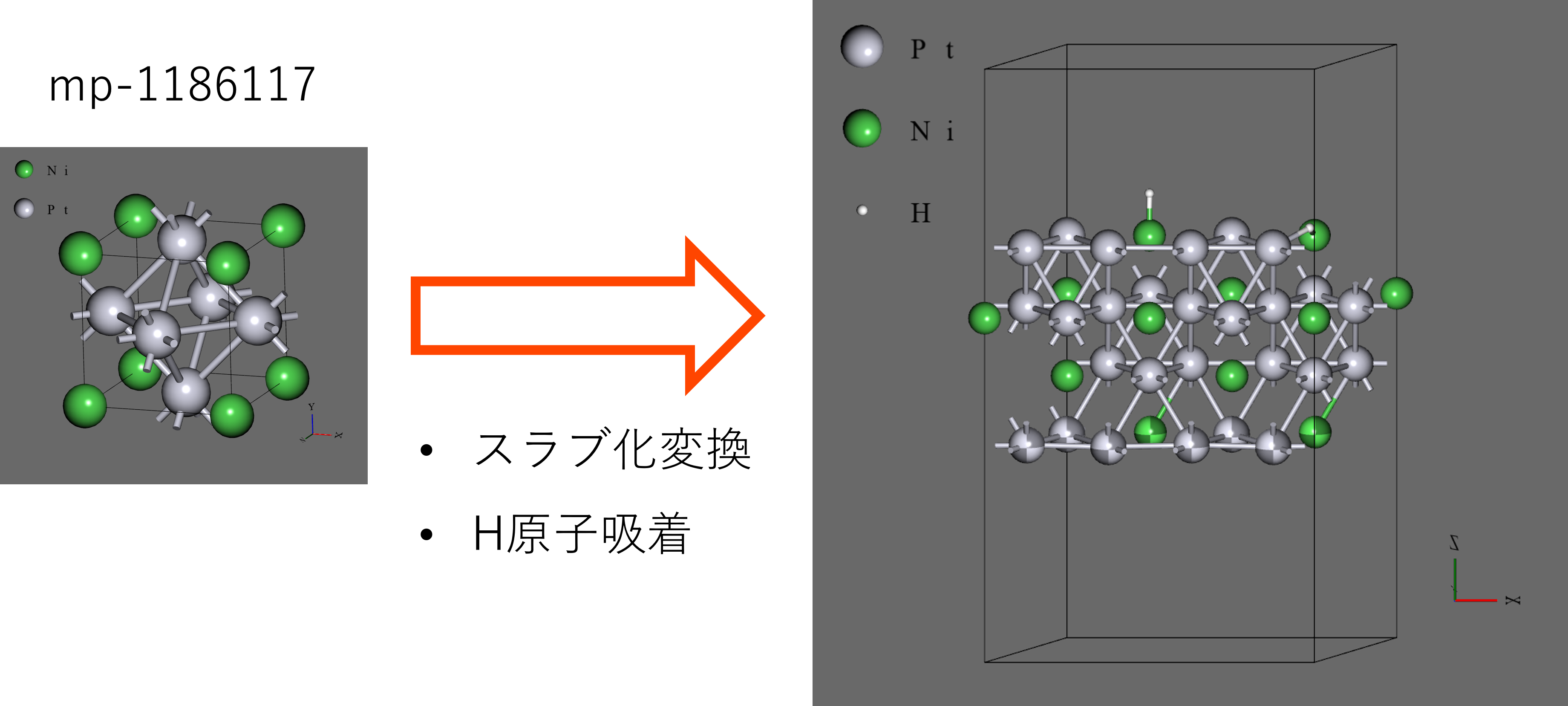
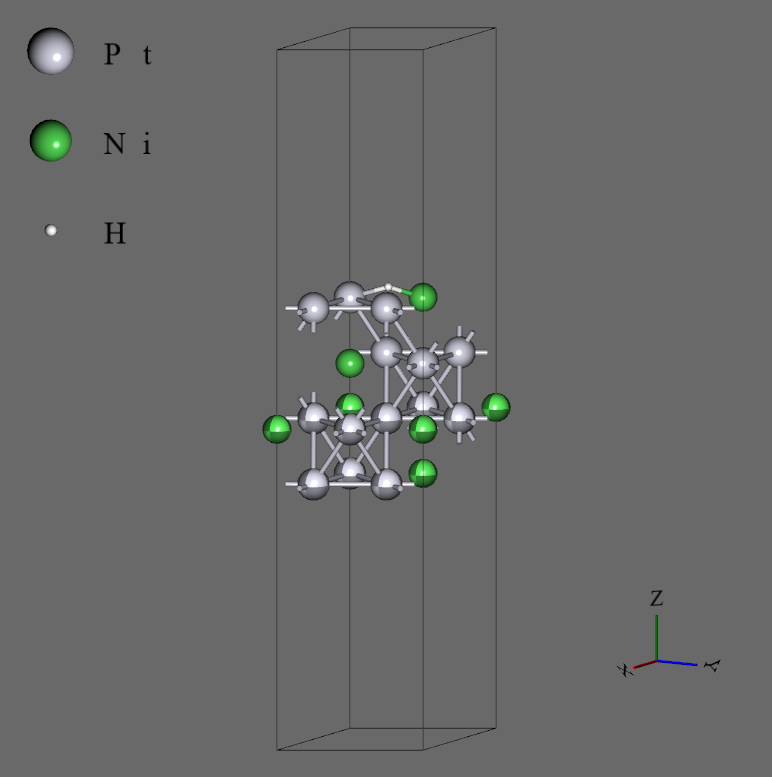
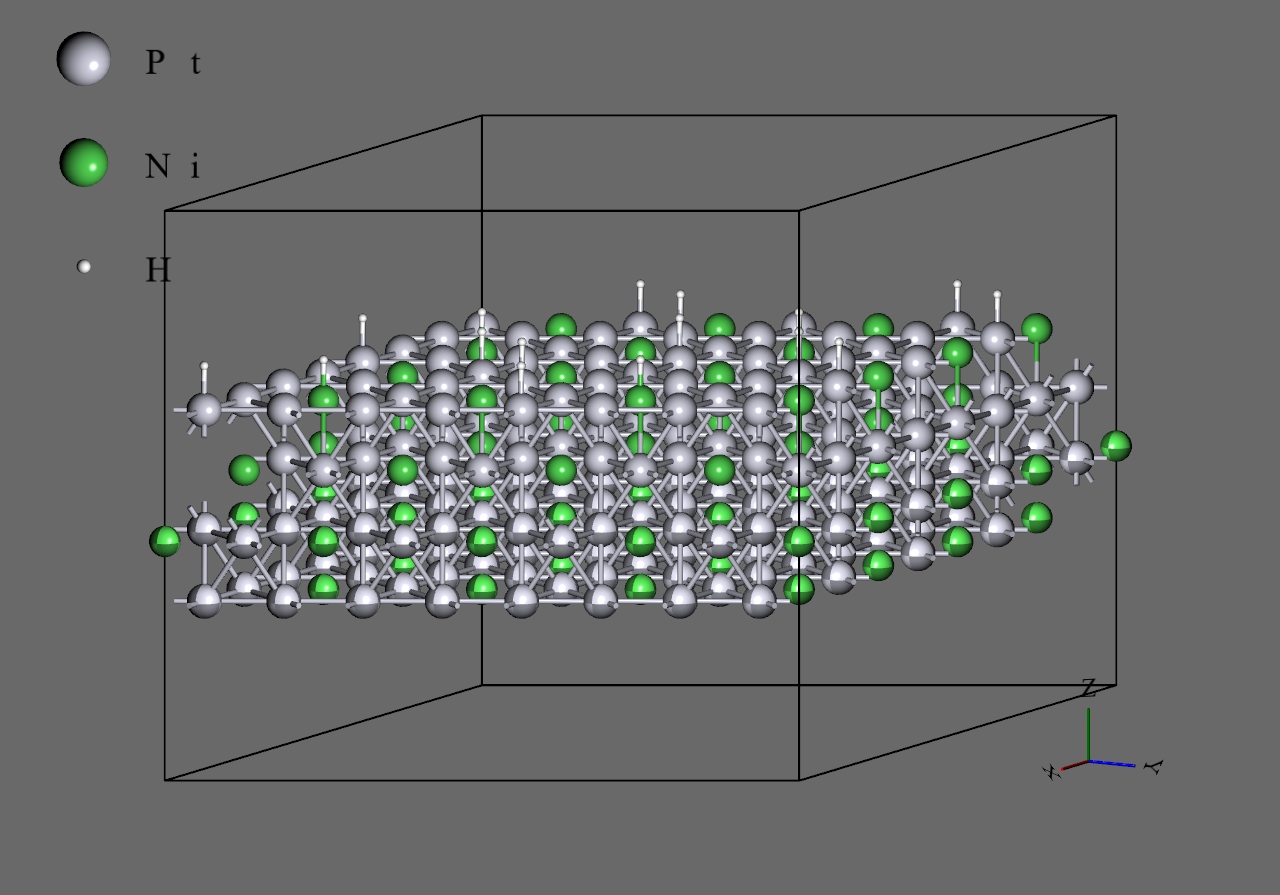
- 初期構造にはMaterials Projectから取得したもの(mp-1186117)を、Advance/NanoLaboの機能を用いて4原子 x 4層のスラブに変換し、構造最適化後にx方向に複製して、水素原子2つを吸着させたもの(34原子系)を用いた。構造の多様性を確保するため、下1層のみを固定した。
- 水素原子の吸着サイトは、Ni上のtopサイト(Ni-top)、Niを含むhcpサイト(Ni-hcp)とした。距離の多様性を持たせるため、実際の吸着距離よりも、topサイトは長く、hcpサイトは短く設定した。
- MD計算は、NPTアンサンブルで行った。初期力場作成のための第一原理MDは200ステップ行い、その後のNNP-MDはSCF計算毎に10 〜 2000ステップ(2.5 〜 500.0 fs)行った。温度は400 Kに設定した。
- SCF計算は、ウルトラソフト擬ポテンシャルを用いた密度汎関数法(DFT)で行った。交換相関汎関数にはGGA-PBEを用いた。カットオフエネルギーは36.0 Ry、k点はy方向に3点とした。また、スピン分極は考慮しなかった。
- ニューラルネットワークの構成は40ノード x 2層とし、活性化関数にはtwisted tanhを用いた。対称関数には80個のChevyshev関数を用い、カットオフ距離は6.5 Åとした。
Intel Xeon Gold 5218 (2 CPU, 32コア)を使用して、約70時間で力場作成が完了した。
- 最終的な教師データ数は、採択されたものと棄却されたものを合わせて1700個になった。
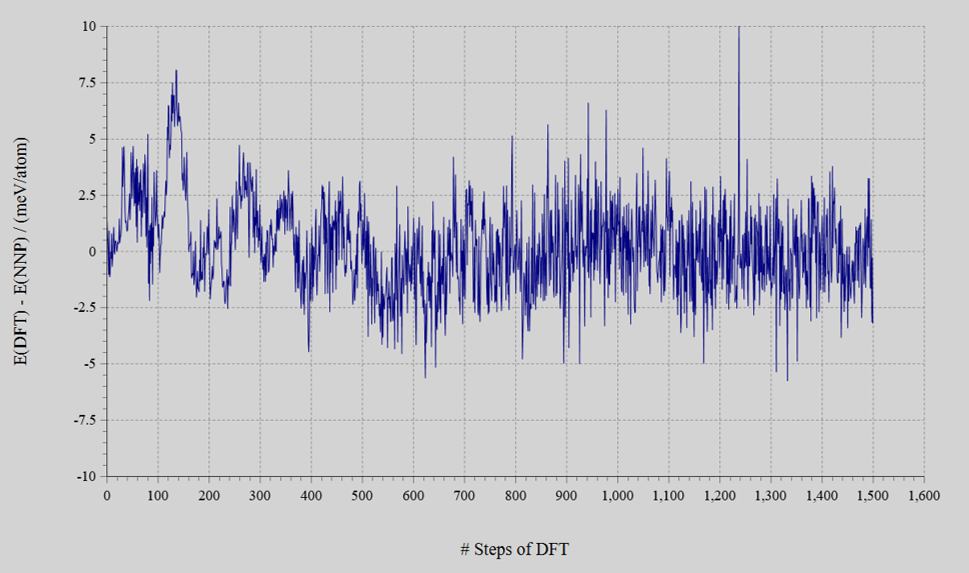
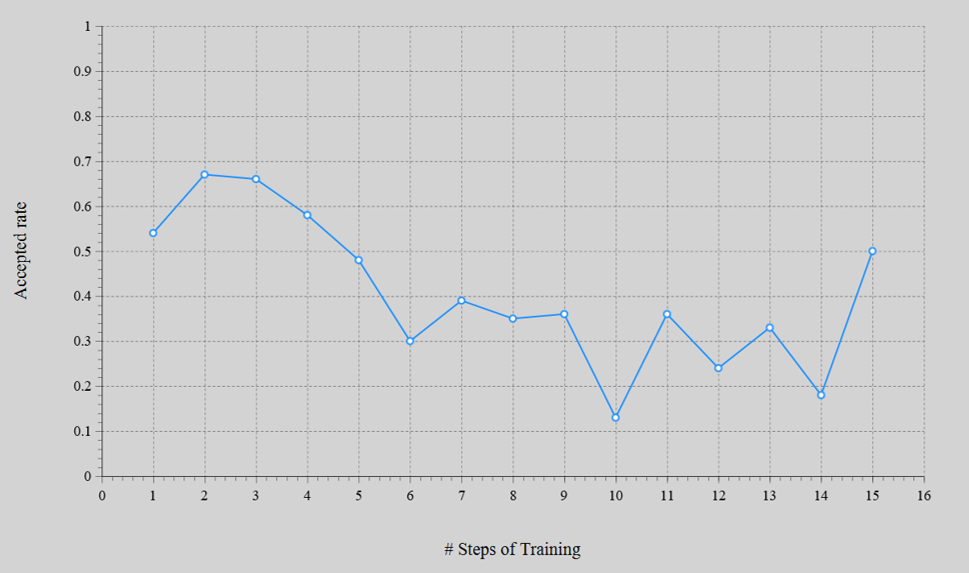
- エネルギーの誤差はMAE = 1.3 meV/atomまで収束した。MC法によるアクセプト率は13 〜 67%の範囲であった。
エネルギーの誤差 EDFT – ENNP

アクセプト率

吸着距離の計算#
NNPを用いたMD計算(NNP-MD)と、DFTによる第一原理計算を用いて構造最適化を行い、各吸着サイトの吸着距離と吸着エネルギーを比較した。
- 構造として4原子 x 4層のスラブを用い、Advance/NanoLaboの機能を用いて、表面に水素原子1つを吸着させたものを用いた。スラブの下2層は原子座標を固定した。
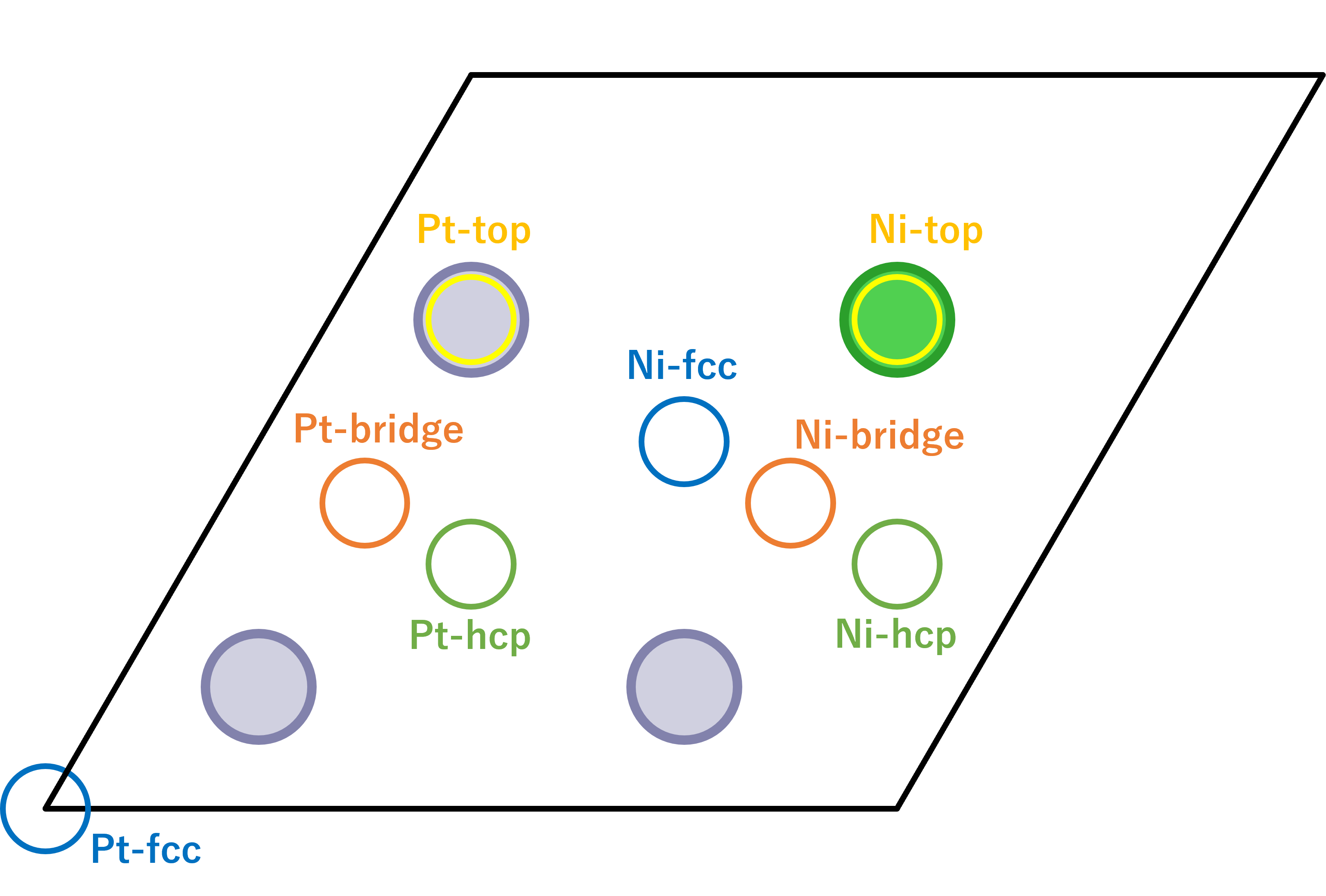
- 吸着サイトは、fcc、hcp、top、bridgeサイトの、それぞれNiを含むサイトとPtを含むサイトの計8種類である。fcc および hcpサイトの吸着はデフォルトで吸着距離が0となっているため、0.5 Å離して初期構造とした。
- 吸着エネルギー計算のため、水素を吸着させていないスラブと、原子状水素についてもそれぞれ構造最適化を行った。
- SCF計算はウルトラソフト擬ポテンシャルを用いた密度汎関数法を用いた。交換汎関数にはGGA-PBEを用いた。カットオフエネルギーは40.0 Ry、k点はxとy方向に3点ずつの計9点とした。スピン分極はCollinearとし、分極率の初期値はNiのみ0.2 μB、PtとHは0.0 μBとした。
- 吸着距離は、第1層の金属原子のz座標平均と、水素原子のz座標との差で算出した。
- 吸着エネルギーは、吸着したスラブの全エネルギーと、スラブ単独と原子状水素の全エネルギーの合計との差で算出した。
4原子 x 4層 スラブ(Ni-fcc)

スラブ上の吸着サイト

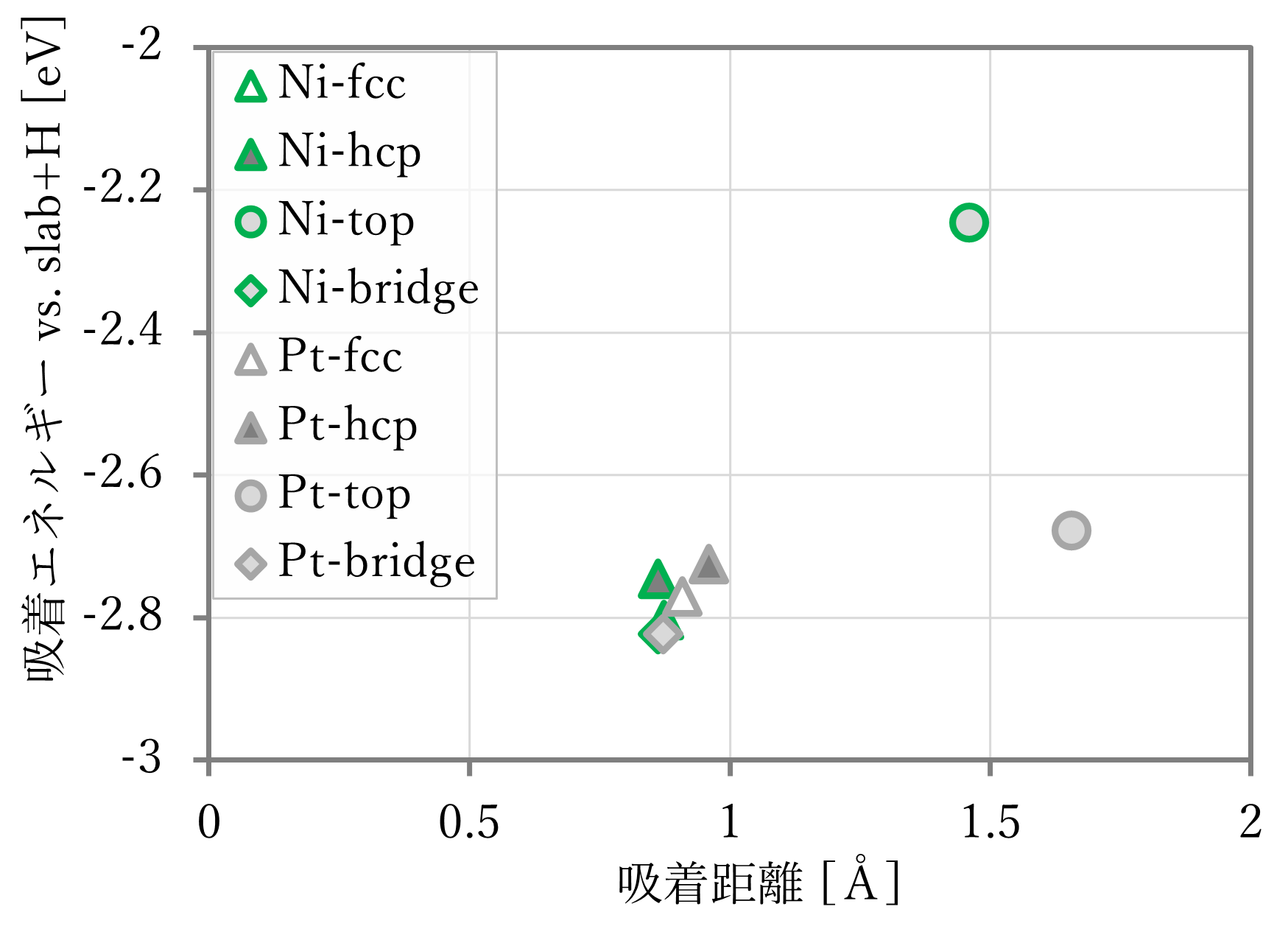
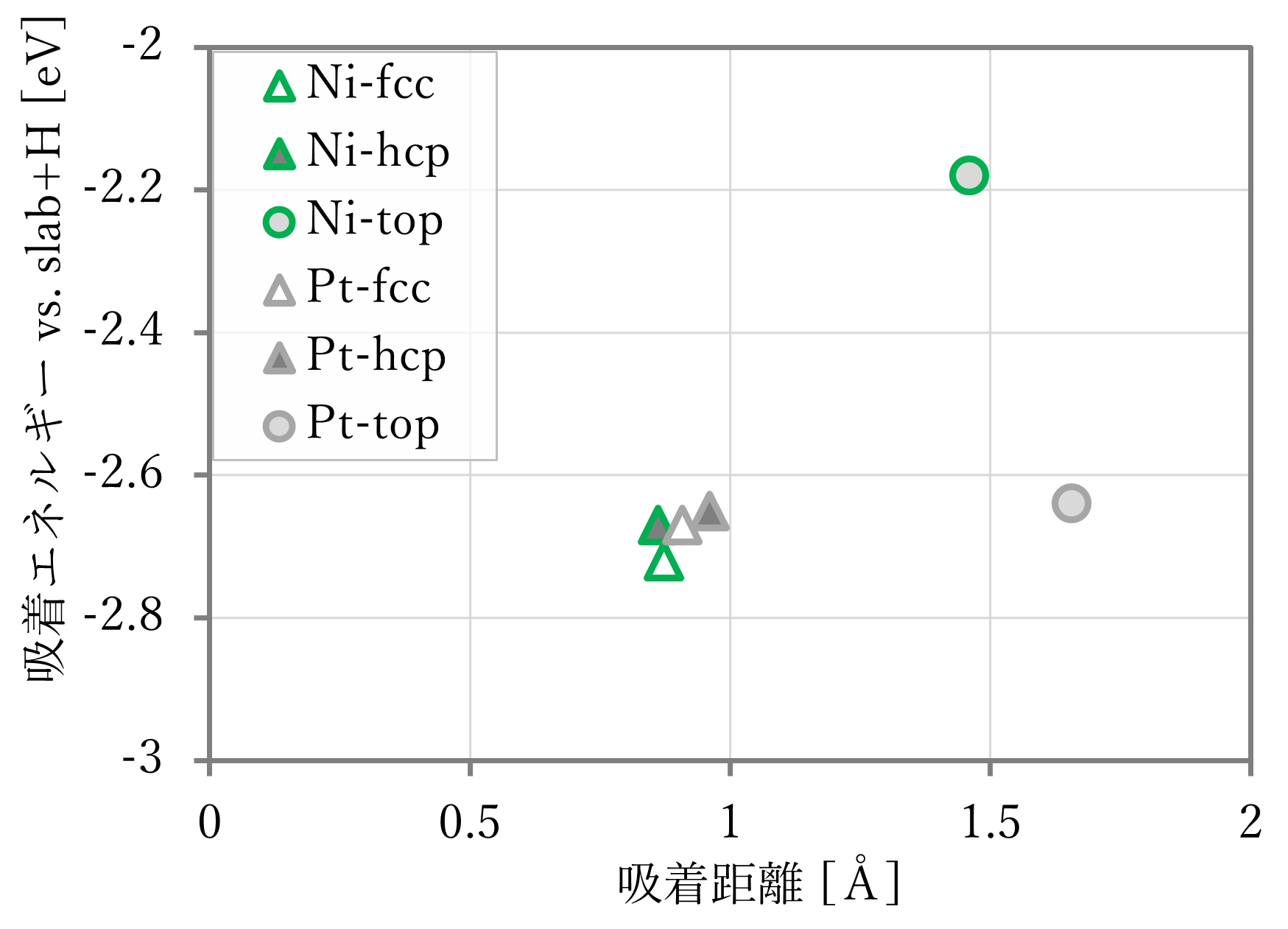
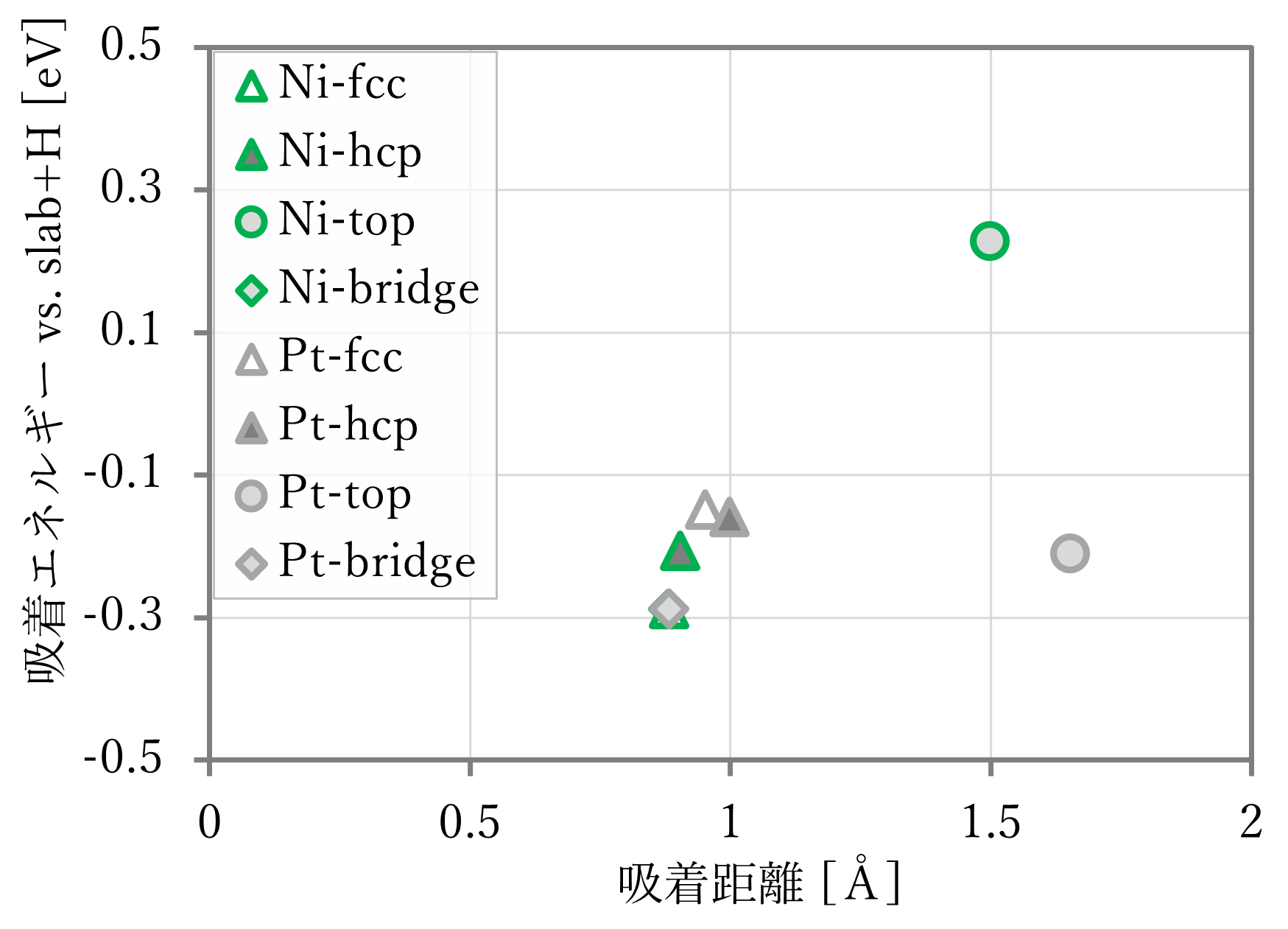
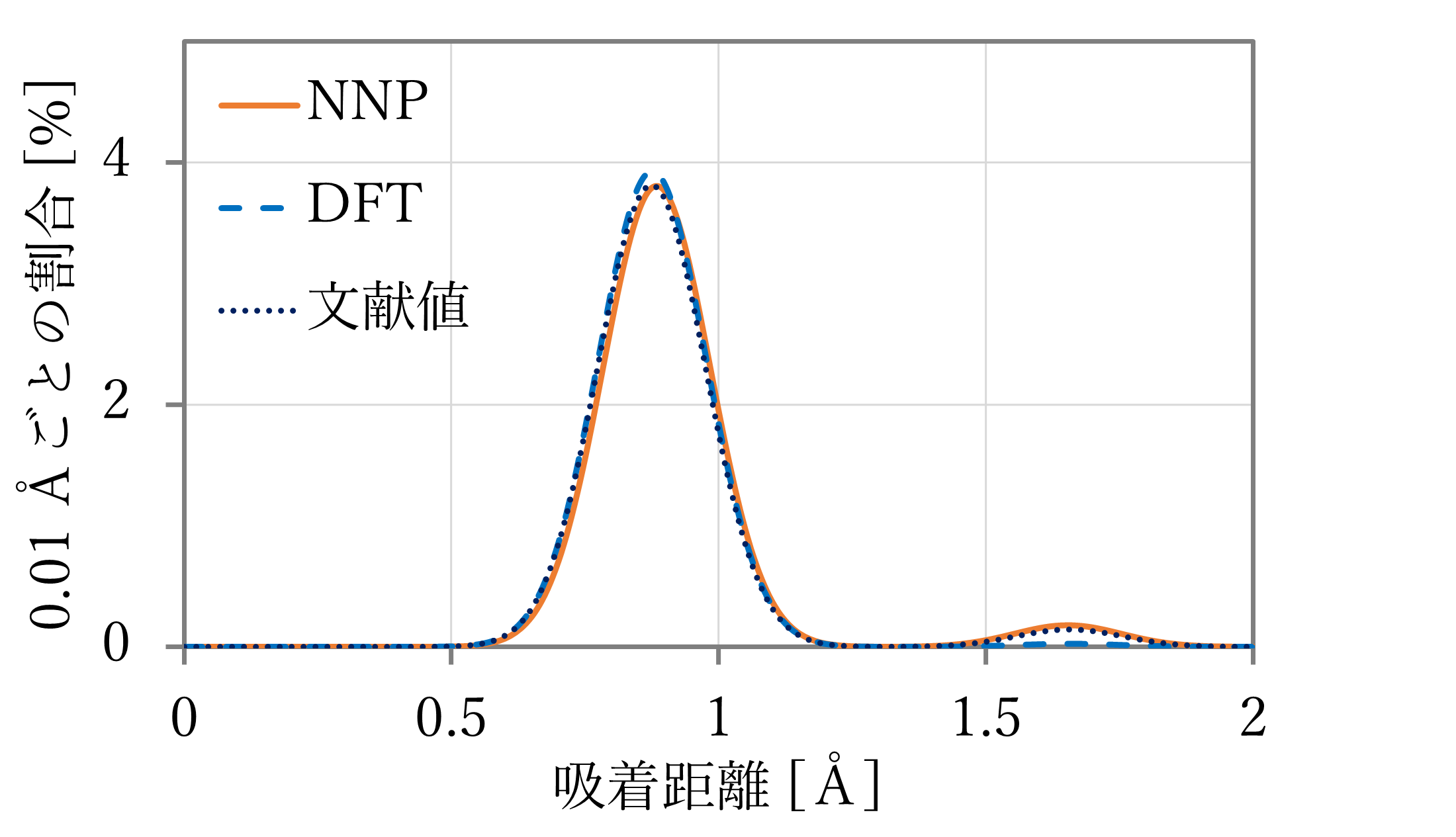
結果は下図表のようになった。右下に文献値[1]も示す。ただし、文献には距離の記載がなかったため、第一原理計算の結果を用いた。
- 吸着距離はよく再現された。
- 吸着エネルギーは概ね再現されているが、NNP-MDと第一原理計算とで値が異なる。これは単独のスラブや原子状水素が教師データに含まれていないためと考えられる。
NNP-MD

分子動力学シミュレーション#
長時間のNNP-MDシミュレーションを行い、水素の吸着距離分布を算出した。
- 構造として、16原子 x 4層のスラブに水素原子4つをtopサイトで吸着させたもの(68原子系)を用いた。また、x方向とy方向に複製して64原子 x 4層としたもの(272原子系)も計算した。どちらも下2層を固定して計算した。
- アンサンブルはNVTとし、Δt = 0.5 fsで200000ステップ(100.0 ps)行った。温度は300.0 Kに固定した。
- 吸着距離は第1層の金属原子のz座標の平均と、水素原子のz座標との差で算出した。
1000ステップ(0.5 ps)毎に座標を出力し、距離を0.01 Åと0.1 Åごとに計数して全体に対する割合を算出した。
16原子 x 4層 スラブ


64原子 x 4層 スラブ

- 計算は、Intel Xeon Gold 5218 (2 CPU, 32コア)を使用して、それぞれ約20分と55分で完了した。同環境で第一原理計算を用い、前節の構造最適化を行った際には、より小さい17原子系にも関わらず45分程度かかっており、NNP-MDが低コストで、かつ高いスケーラビリティを持つことがわかる。
- 結果は下図左のようになった。0.01 Åごとの値を青線で、0.1 Åごとの値を橙線で示す。
-
加えて、前節の吸着距離・エネルギー計算の結果をBoltzmann分布に当てはめ、σ2 = 0.01の正規分布関数で分散させた場合の距離分布を下図右に示す。
前節同様、文献値の距離には第一原理計算の結果を用いた。また、NNPおよび第一原理計算において、bridgeサイトは全てhollowサイトに変化していたため除外した。
- 計算の結果、それぞれ0.9 Åと1.1 Å付近が最も多く、また、どちらの結果においても1.6 Å付近のtopサイトと見られる距離にも一定数が存在した。文献値と比較すると、hollowサイト付近は距離が離れているが、量の大小関係が、特に64原子 x 4層系においてよく再現された。
- Boltzmann分布に従う分布と比較すると、NNP-MD計算の結果では、hollowサイトとtopサイトとの間にも多くの構造が観察されたことがわかる。これは、前節の計算が対称性が高く安定したサイトに限って行われたために生まれた違いと考えられる。NNP-MD計算を使えば、正確なエネルギー予測に基づいて、様々な状態を含んだより実際の系に近い計算結果を得ることができる。
16原子 x 4層 + 4H
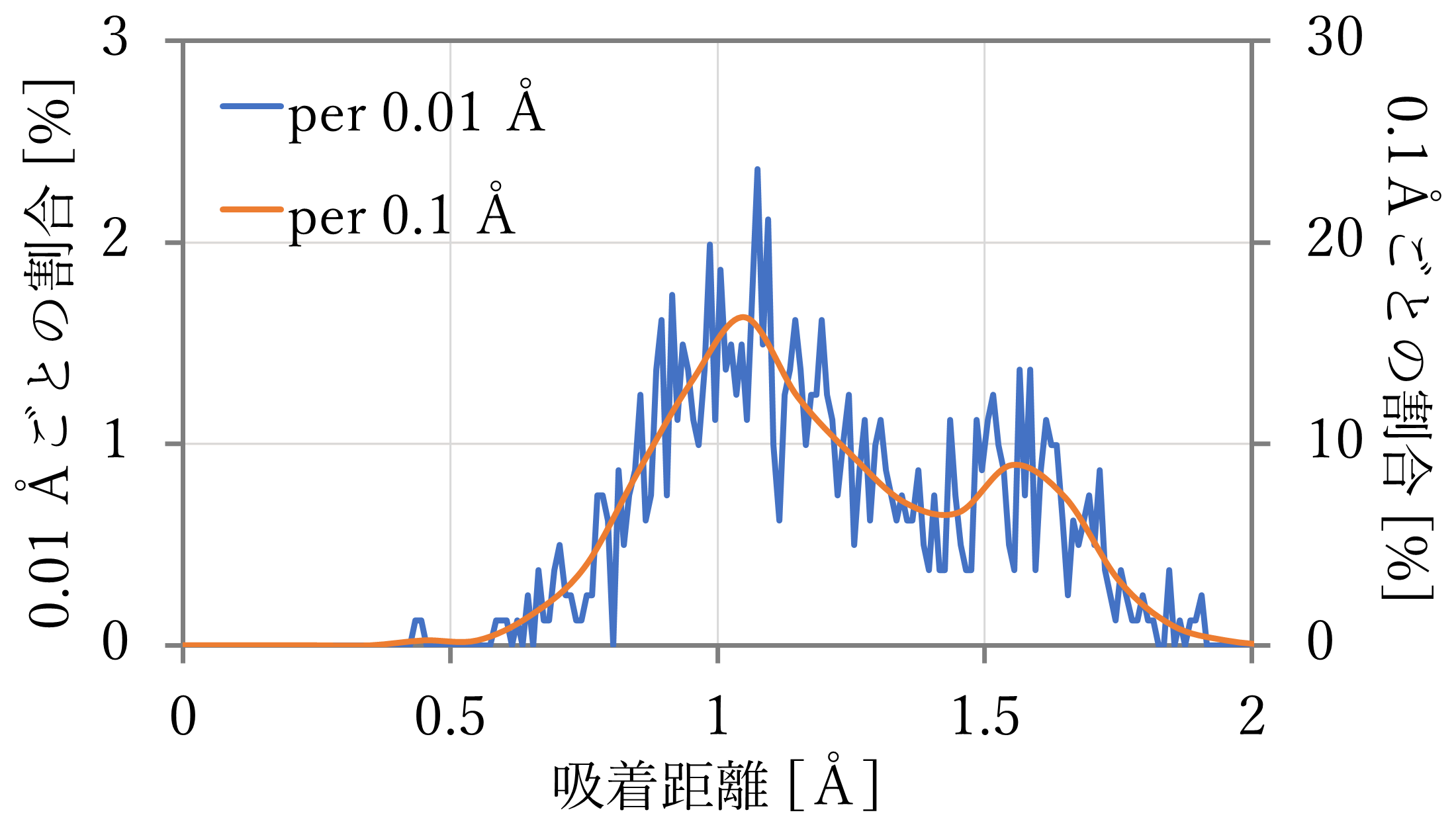
64原子 x 4層 + 16H
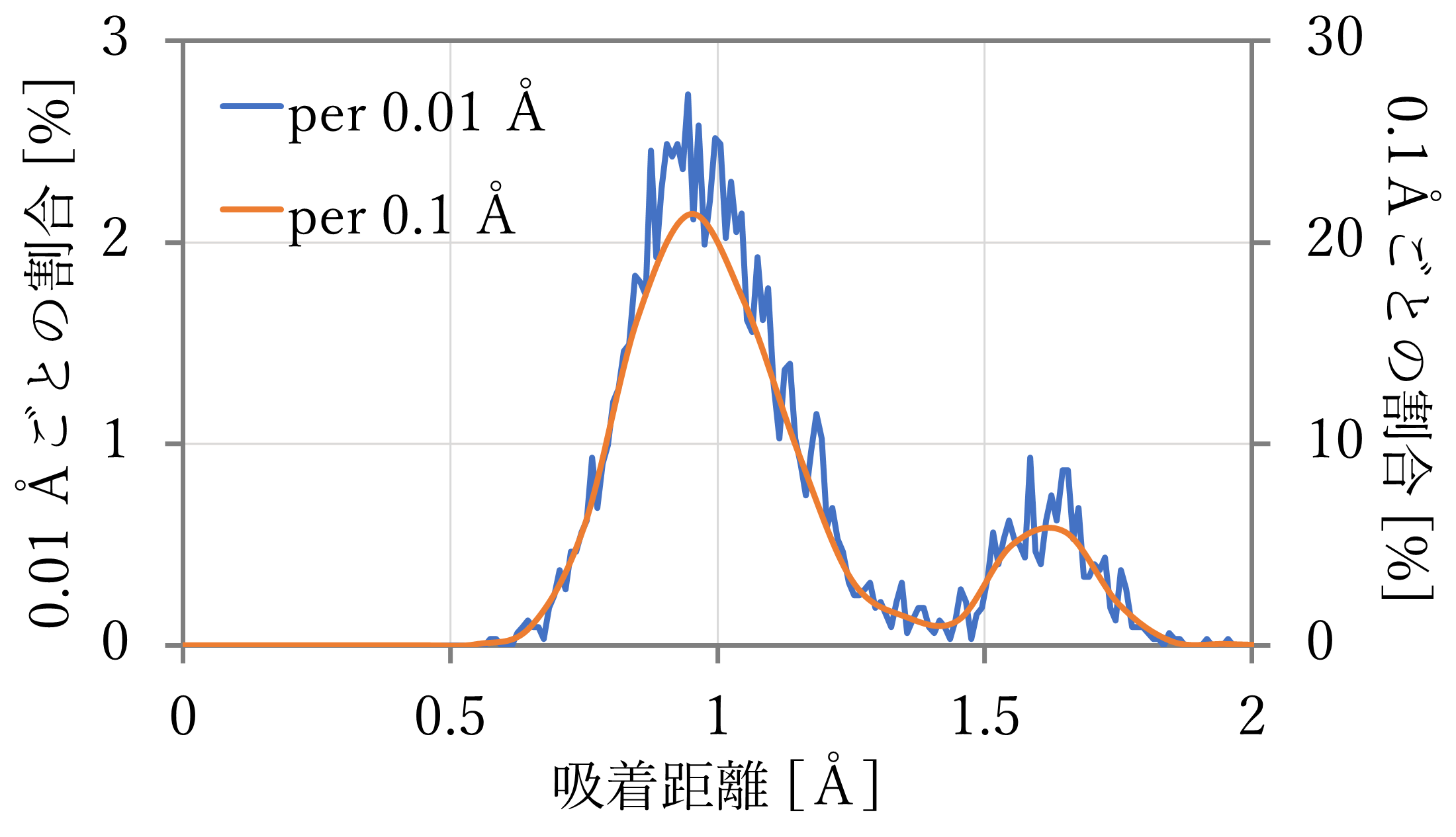

64原子 x 4層 + 16H

構造最適化計算に基づくBoltzmann分布

関連ページ#
- ニューラルネットワーク分子動力学システム Advance/NeuralMD
- 解析分野:ナノ・バイオ
- 産業分野:材料・化学
- Advance/NeuralMD 製品案内
- Advance/NeuralMD ドキュメント
-
S.Zhang et al., Topics in Catalysis, 2020, 63, 714–727 ↩