コンテンツにスキップ

Prediction of volume dependence of total energy by cooperation function with Python#

You can execute various operations via Python scripts on Advance/NanoLabo. Using Python scripts enables you to automate complicated workflows.

We analyzed unit-cell volume dependence of total energy of single-crystal Ge. We generated 31 models with different volume and analyzed calculation results using Python scripts.

Warning

We put sample code1 on this page to introduce cooperation function with Python of Advance/NanoLabo, but we don’t guarantee their operations. Please see the online manual for information on how to use the cooperation function with Python.

Generation of models with different volume#

Optimized structure of single-crystal Ge
Optimized structure of single-crystal Ge

First, we imported optimized structure of single-crystal Ge2 into Python and created a new project. Next, we scaled unit-cell of the project isotropically3. By repeating this procedure with changing scale, we generated 31 models with different volume.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
import nanolabo
import numpy as np

#Generate 31 models whose unit-cell volumes are scaled as 0.80, 0.81, ... 1.09, 1.10.
N = 31
scale_list = np.linspace(0.8, 1.1, N)

for idx, scale_volume in enumerate(scale_list):
    #Import optimized structure (Ge-Optimized.cif) and generate new project.
    #Name projects as Ge-0, Ge-1, ... Ge-29, Ge-30.
    prj_name = f'Ge-{idx}'
    nanolabo.create_project('Ge-Optimized.cif', prj_name)

    #Scale unit-cell isotropically
    lattice = nanolabo.get_lattice(prj_name)
    lattice = np.array(lattice) * scale_volume ** (1./3.)  
    nanolabo.set_lattice(prj_name, lattice)
    nanolabo.save_project(prj_name)

Execution of calculation#

We executed calculation by calling run_project function and specifying project name. 

1
2
3
for idx, scale_volume in enumerate(scale_list):
    prj_name = f'Ge-{idx}'
    nanolabo.run_project(prj_name, 'SCF')
List of finished/running/waiting calculation jobs

Analysis of volume dependence#

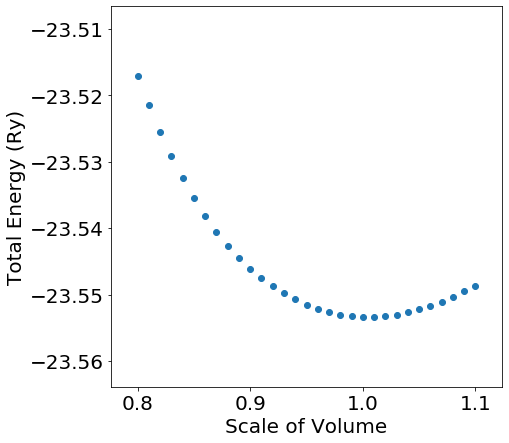
After the calculations finished, we got the total energy of each model by calling qe_get_total_energy function and plotted the results in the figure, in which the horizontal axis corresponds to the scale of volume and the vertical axis corresponds to the total energy.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
#Load total energy of each model into list.
energy_list = [None] * N
for idx, scale in enumerate(scale_list):
    prj_name = f'Ge-{idx}'
    nanolabo.open_project(prj_name)
    converge, energy = nanolabo.qe_get_total_energy(prj_name)
    energy_list[idx] = energy if converge else None
    nanolabo.close_project(prj_name)

#Plot volume dependence of total energy.
import matplotlib.pyplot as plt

plt.scatter(scale_list, energy_list)
plt.show()
Volume dependence of total energy

In comparison with the equilibrium structure, if scale of volume is in a range of , total energy change is below . Also, we can see from the result that total energy increases by compared with the equilibrium structure when volume is compressed by .

Such an analysis of volume dependence of total energy enables you to predict physical properties like volume elasticity and transition pressure.

関連ページ#

  1. The sample code was written assuming since Python3.7. NumPy and Matplotlib were used in the sample code. For infomation of these, please visit each official website. ↩

  2. We carried out structural optimization on Advance/NanoLabo and saved the result as Ge-Optimized.cif beforehand. ↩

  3. You can edit not only unit cell but also atomic coordinates via Python scripts. ↩