鉄単結晶の分子動力学シミュレーション#

ナノ材料統合GUI Advance/NanoLaboを用いた鉄（Fe）単結晶の分子動力学シミュレーション¹の解析事例について紹介します。

紹介する事例は、モデルの作成からジョブの投入・結果の解析に至る一連のプロセスをすべてAdvance/NanoLabo上で行うことができます。

計算モデルの作成#

解析対象として鉄（Fe）の単結晶を用います。鉄は標準状態下で体心立方格子（bcc）が最も安定な結晶構造となります。本事例では鉄単結晶（bcc）の単位格子をもとに、セルサイズ22.8Å×22.8Å×22.8Å、1024原子系の超格子モデルを作成しました。

次に力場や統計的アンサンブルといった計算条件の設定を行います。

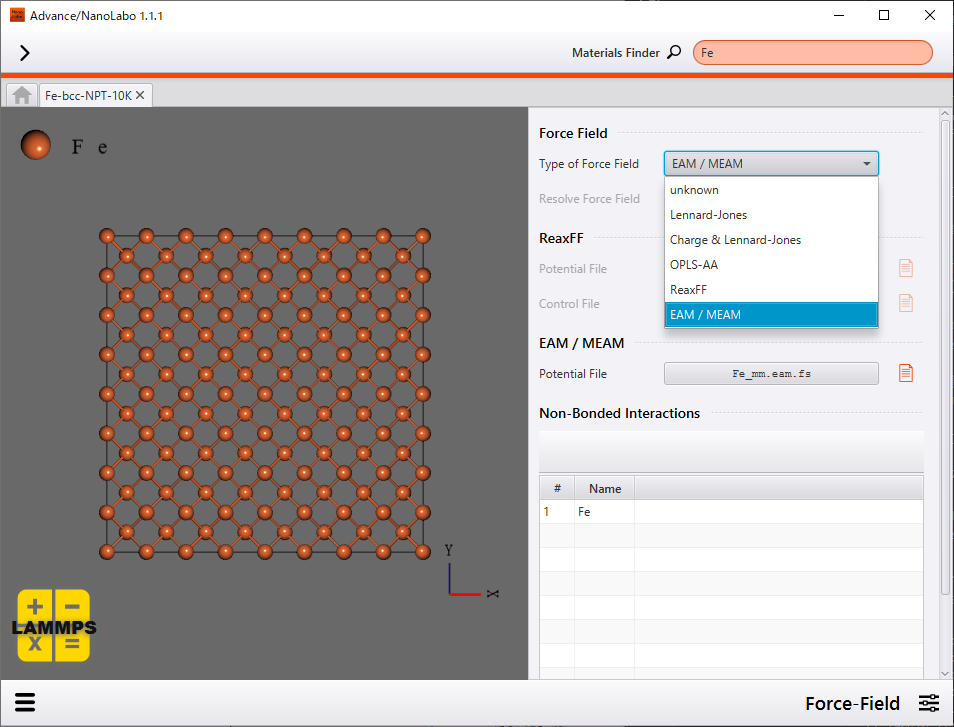
力場には原子挿入法（Embedded Atom Method; EAM）ポテンシャルを採用しています。EAMポテンシャルには、引力項・斥力項といった2体ポテンシャルのほかに、周辺原子が形成する電子密度の中に原子を埋め込むことで生じる項（多体項）が含まれます。EAMポテンシャルは金属結合系の分子動力学計算で主に利用されています。

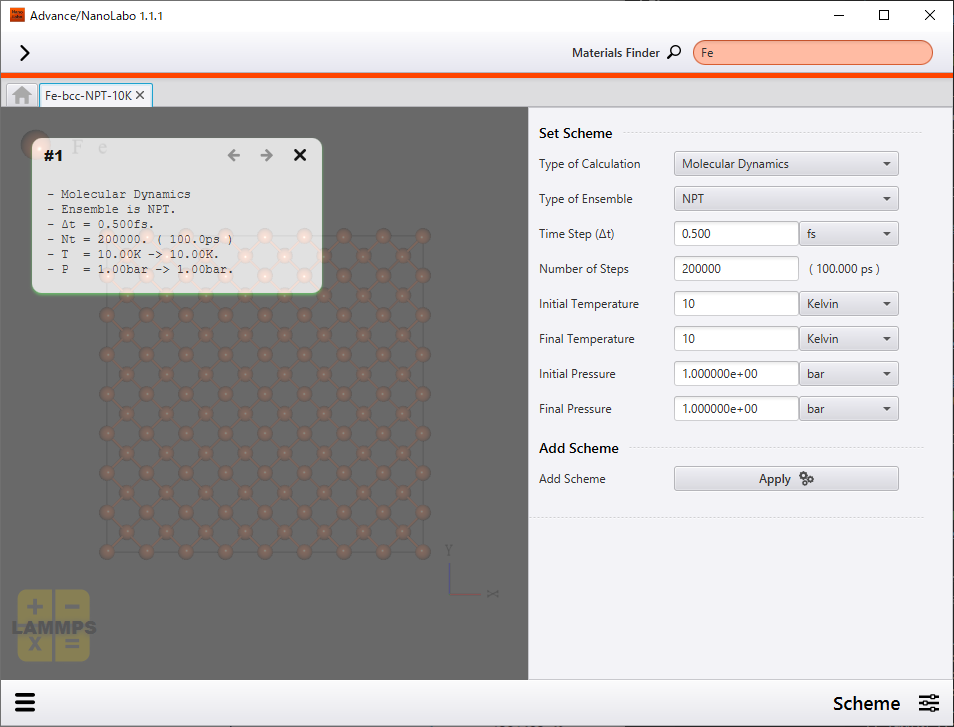
統計的アンサンブルには温度と圧力が一定のNPTアンサンブルを採用しています。温度と圧力を一定に保つための手法として、能勢-アンダーセンの方法などが用いられます。能勢-アンダーセンの方法では、仮想的な熱浴とピストンによる項をハミルトニアンに導入して、温度と圧力が一定になるように制御します。

シミュレーション時間の条件については、時間の刻み幅を0.50fs、ステップ数を200000に設定しました。これは実時間では100psに相当します。


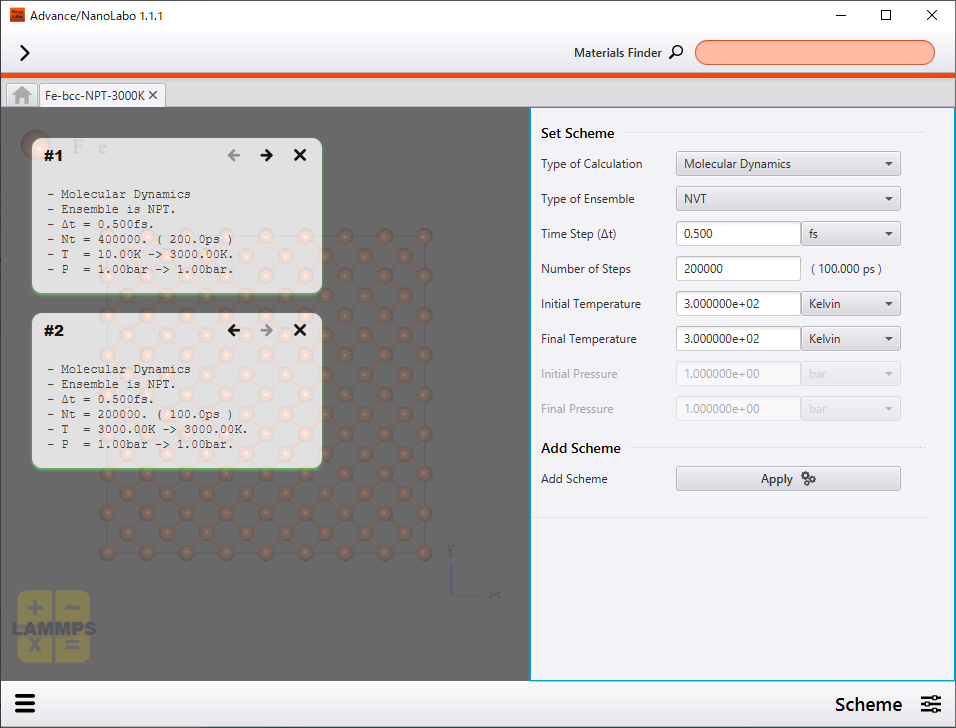
Fe単結晶1024原子モデル	力場の設定	計算スキームの設定

解析結果#

複数の異なる温度のもとで行った動力学計算の結果を示します。圧力はすべて1barとしています。

NPT（10K）#

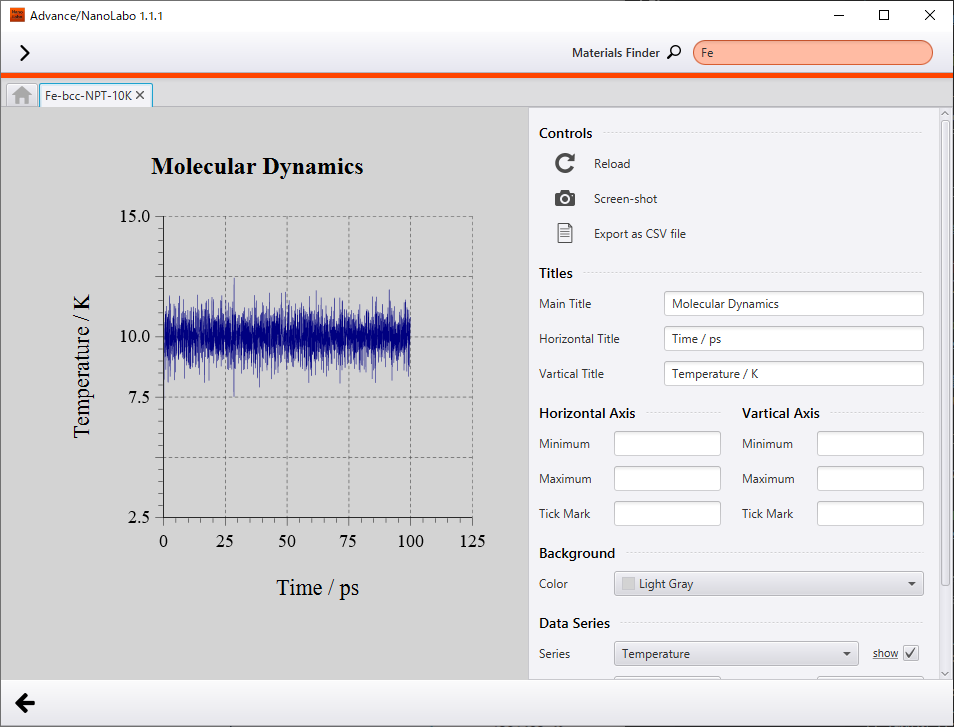
温度10K・圧力1barの条件下でNPTシミュレーションを行った結果を示します。温度は10Kに、密度は8.0g/cm³にそれぞれ収束しています。低温であるため、原子は結晶格子内の平衡位置近傍でわずかに振動しています。


温度の変化	密度の変化

結晶構造の変化のアニメーション

NPT（300K）#

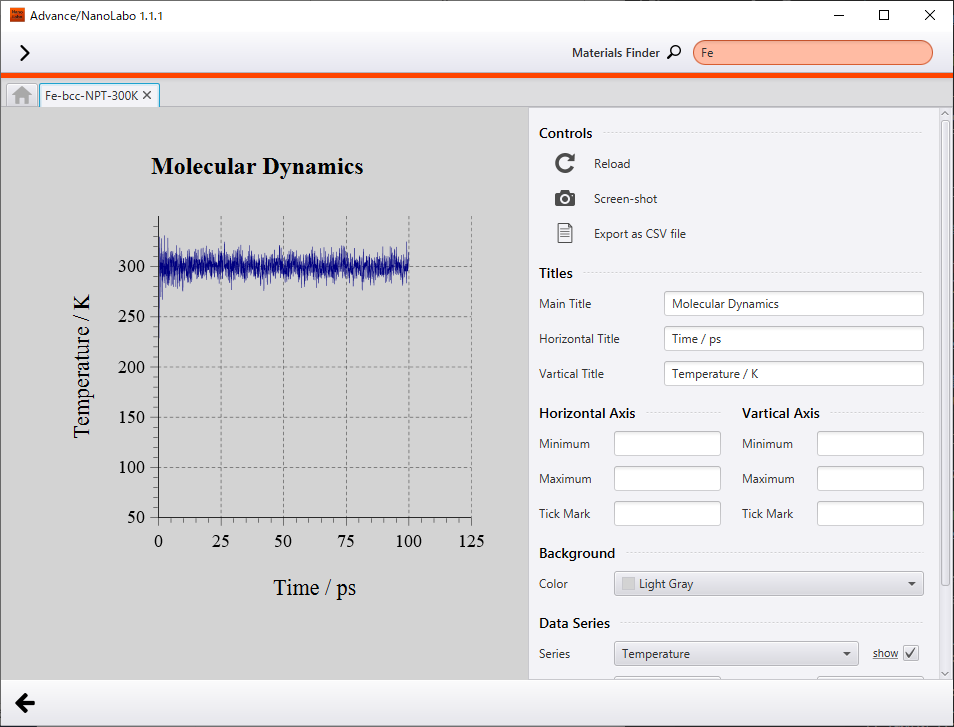
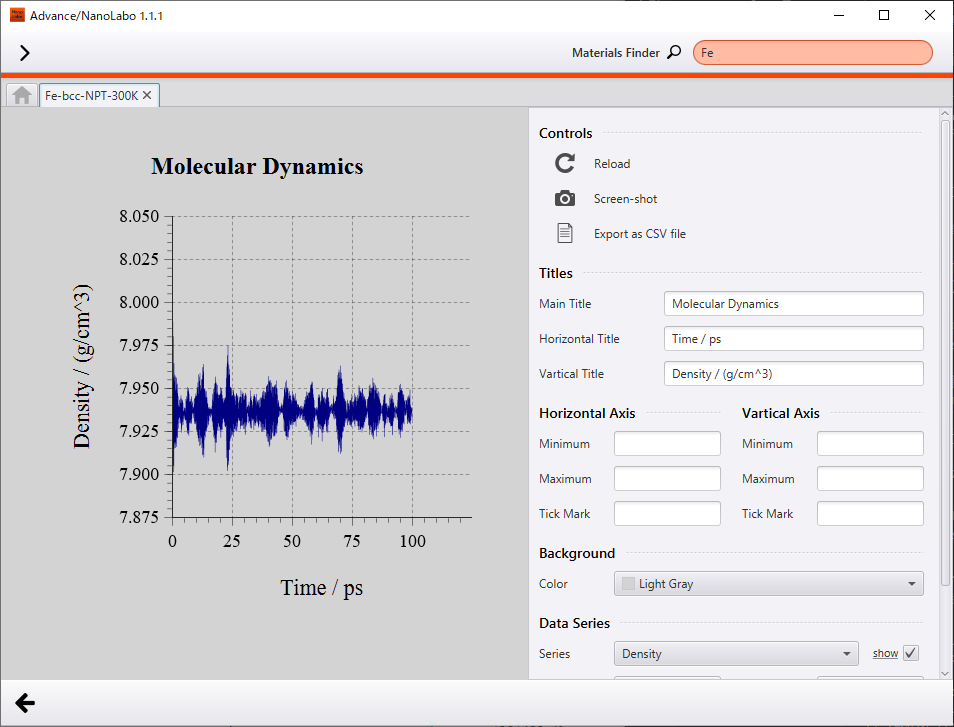
次に、温度300K・圧力1barの条件下でNPTシミュレーションを行った結果を示します。温度は300Kに、密度は7.9g/cm³にそれぞれ収束しています。温度10Kの結果と比較すると、原子の振動はやや激しくなっていますが、結晶構造は保たれています。

標準状態における鉄の密度は7.87g/cm³²であり、計算値は実験値とよい一致を示しています。


温度の変化	密度の変化

結晶構造の変化のアニメーション

NPT（10K→3000K）#

最後の例として、0Kから3000Kまで200psかけて一定の温度上昇速度で系の温度を上昇させ、その後に100psの間だけ系の温度を3000Kに保つようなシミュレーションの結果を示します。Advance/NanoLaboではこのように同一のモデルに対して異なる計算スキームを連続して適用することが可能です。

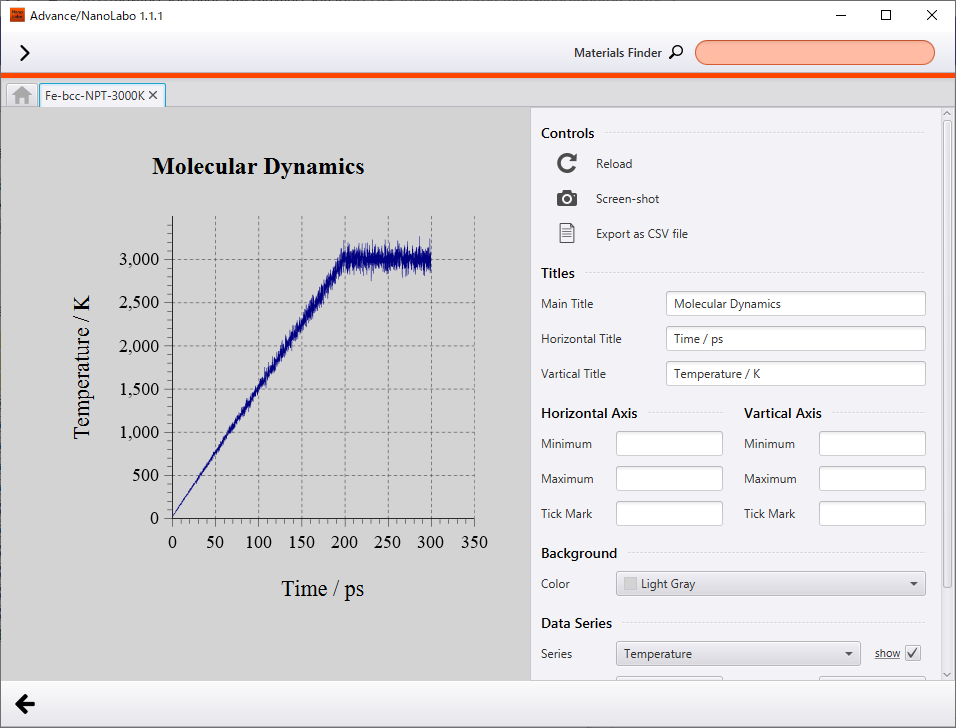
最終的に温度は3000Kに、密度は6.4g/cm³にそれぞれ収束しています。全体として、温度が上昇するにつれ、格子が膨張し密度が低下する傾向がみられます。また、シミュレーション結果のアニメーションを解析すると、温度の上昇に伴い格子内での原子の振動が激しくなり、最終的に結晶構造が壊れていることが分かります。

密度変化の最も特徴的な点として、140ps近傍（系の温度は約2100K）の不連続な変化が挙げられます。ポテンシャルエネルギー変化のプロットにも同様に140ps近傍の不連続な変化がみられます。結晶構造のアニメーションと比較すると、この不連続な点は原子の振動が激しさを増し結晶構造が壊れはじめるタイミングと一致します。これは固体から液体への相転移が起こっていると解釈できます。なお、鉄の融点（実験値）は1811K³なので、本計算事例において鉄の融点は300Kほど大きく見積られています。


計算スキームの設定	温度の変化	密度の変化

ポテンシャルエネルギーの変化

結晶構造の変化のアニメーション

鉄単結晶の分子動力学シミュレーション#

計算モデルの作成#

解析結果#

NPT（10K）#

NPT（300K）#

NPT（10K→3000K）#

関連ページ#