コンテンツにスキップ

Molecular dynamics simulation of single-crystal iron#

Snapshot of molecular dynamics simulation

We introduce molecular dynamics simulation1 of single-crystal iron (Fe) with Advance/NanoLabo, an integrated GUI for nanomaterials.

The entire process from modeling to running calculation and analysis of results was executed on Advance/NanoLabo.

Generation of calculation model#

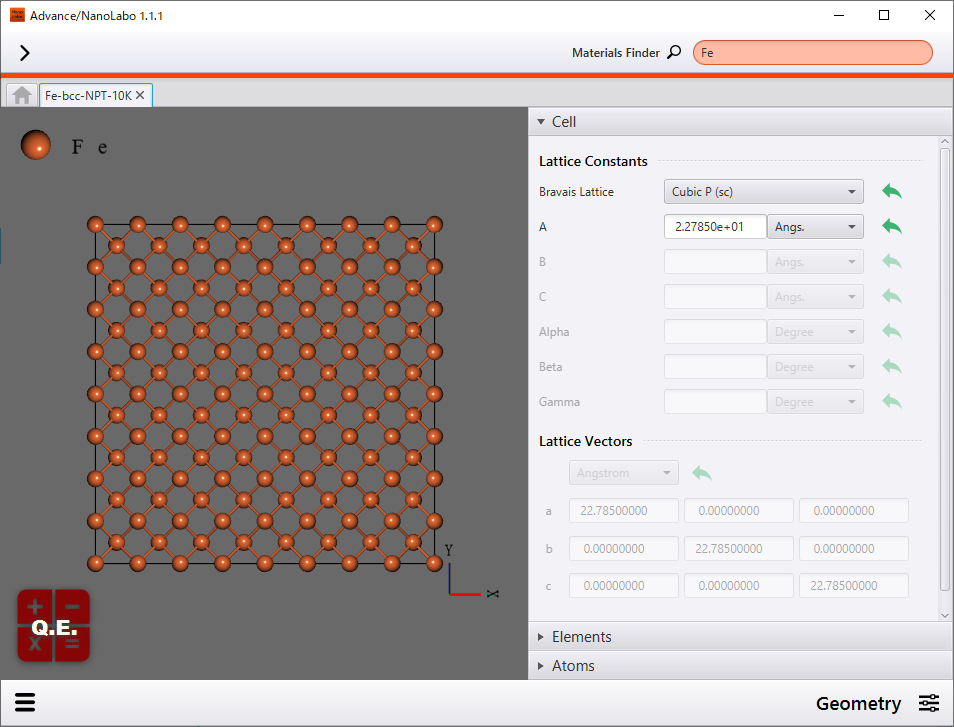
We analyzed single-crystal Fe. It is known that Fe crystal adopt the body-centered-cubic (bcc) structure under standard conditions. We built super cell model which has repeating Fe unit cell structure. The super cell contains 1024 atoms and its size is 22.8Å×22.8Å×22.8Å.

Next, we set calculation conditions like force-field and statistical ensemble.

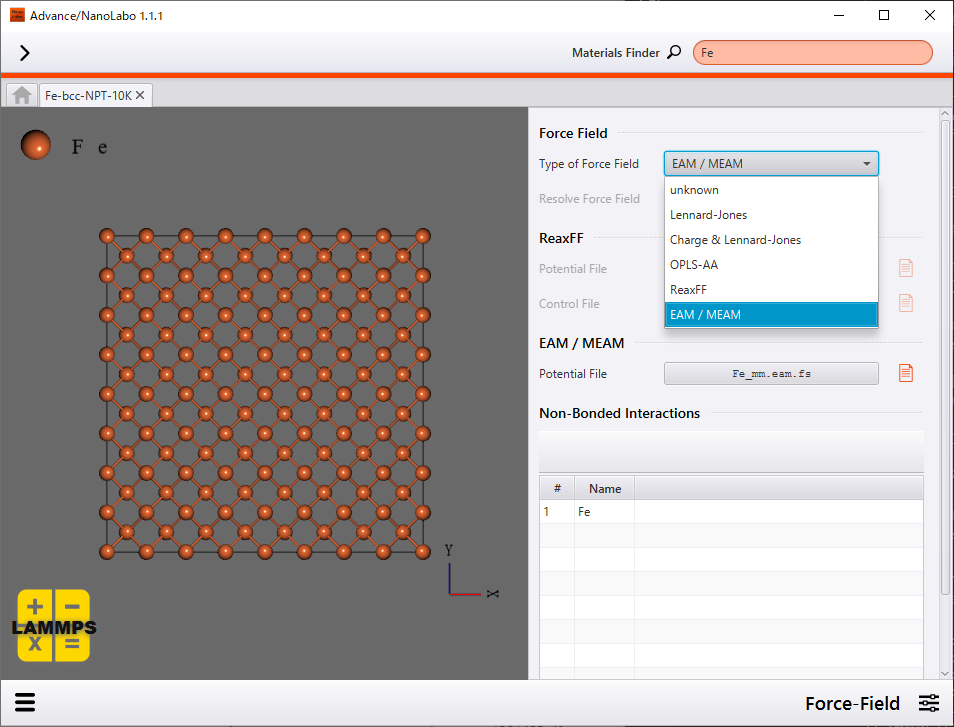
We adopted embedded-atom-method (EAM) potential as force-field. EAM potential contains many-body terms which originate from embedding atoms in electron density formed by surrounding atoms in addition to two-body terms such as attractive term and repulsive term. EAM potential is mainly used for molecular dynamics simulation of metallic bond systems.

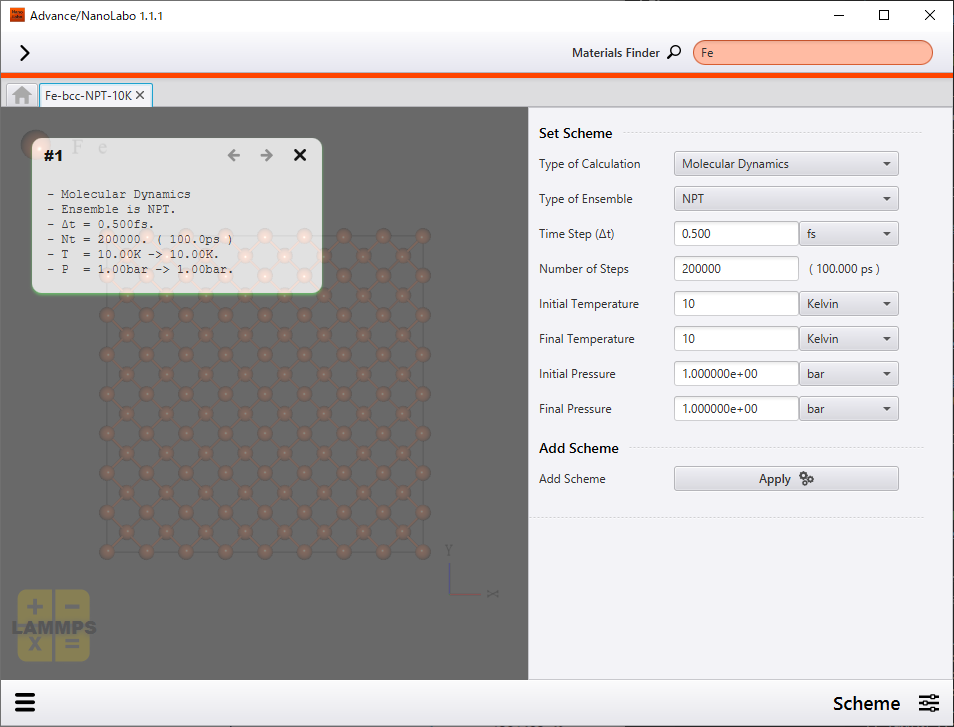
We employed NPT ensemble in which pressure and temperature are constant as statistical ensemble. The Nose-Andersen method was used to keep pressure and temperature constant. In Nose-Andersen method, terms which arise from virtual heat bath and piston are introduced to Hamiltonian to keep pressure and temperature constant.

We set simulation time step as 0.50 fs and number of steps as 200000. Simulation time is 100 ps in this setting.

Single-crystal Fe model (1024 atoms) Setting of force-field Setting of calculation scheme
Single-crystal Fe model
(1024 atoms)
Setting of force-field
Setting of calculation scheme

Analysis results#

We show results of molecular dynamics simulations executed under several different temperature. Pressure was set as 1 bar in all simulations.

NPT（10K）#

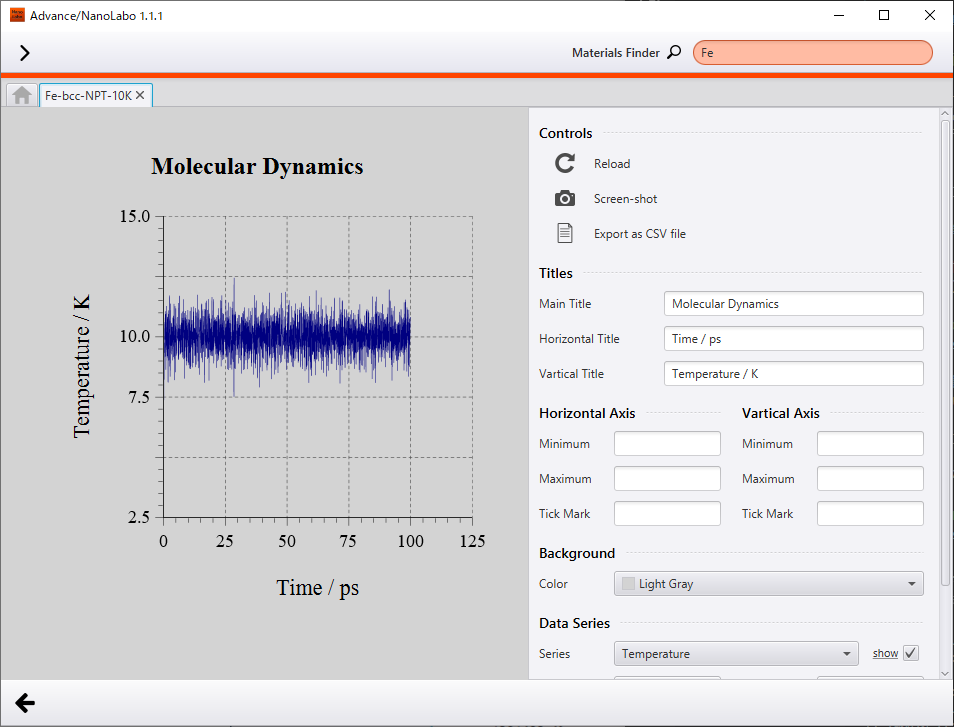
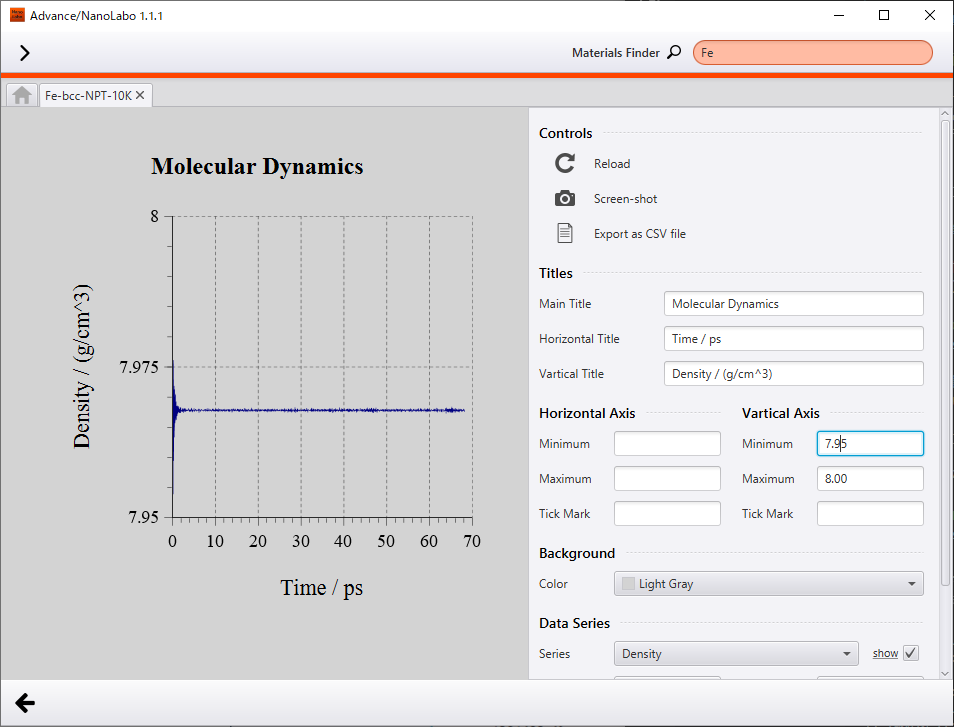
Firstly, we show results of NPT simulation executed under 10 K and 1 bar. Temperature converged to 10 K and density converged to 8.0 g/cm3. Because of low temperature condition, atoms oscillate slightly around equilibrium point of the crystal lattice.

Change of temperature Change of density
Change of temperature
Change of density
Animation of change of crystal structure

NPT（300K）#

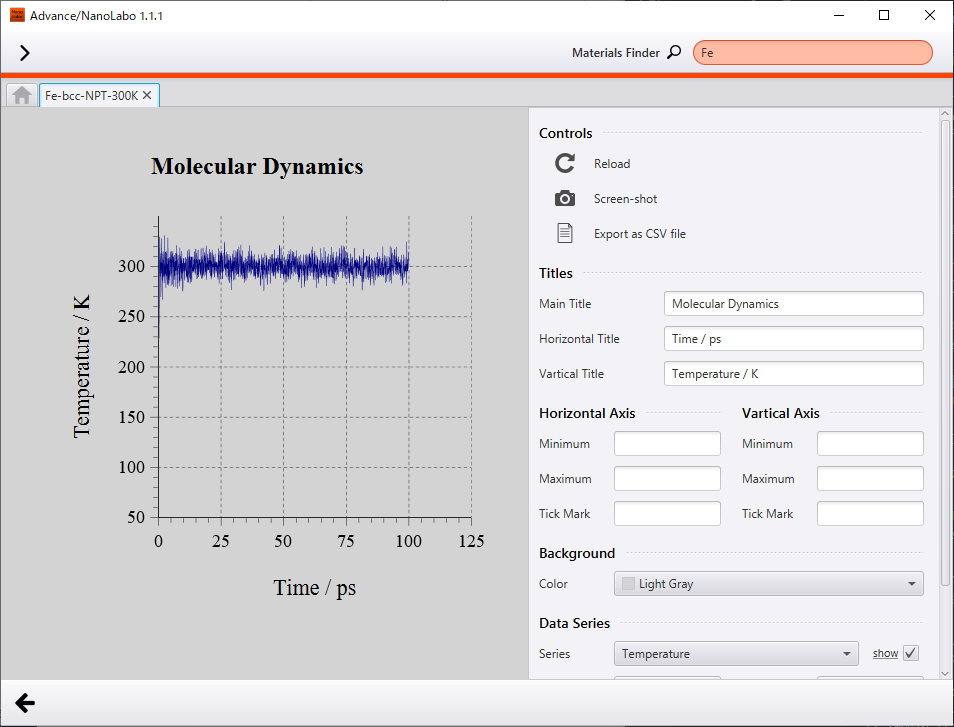
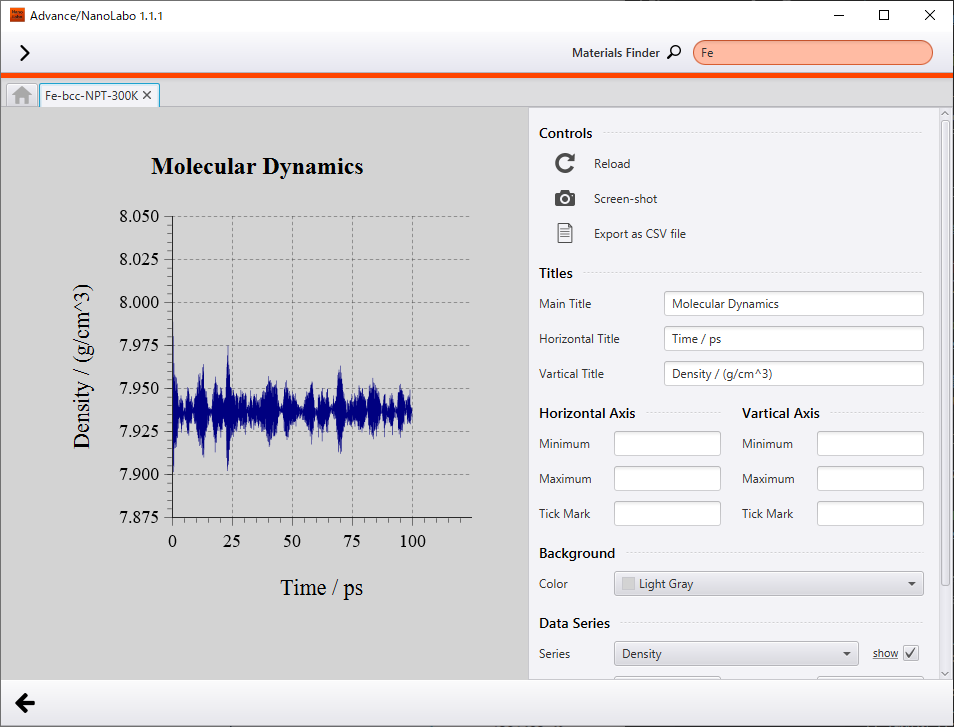
Secondly, we show results of NPT simulation executed under 300 K and 1 bar. Temperature converged to 300 K and density converged to 7.9 g/cm3. As compared to result at 10K, atomic oscillation is somewhat intense, but crystal structure is kept. Density of Fe under standard condition reported experimentally is 7.87 g/cm3 2 and the calculated value is comparable with the experimental value.

Change of temperature Change of density
Change of temperature
Change of density
Animation of change of crystal structure

NPT（10K→3000K）#

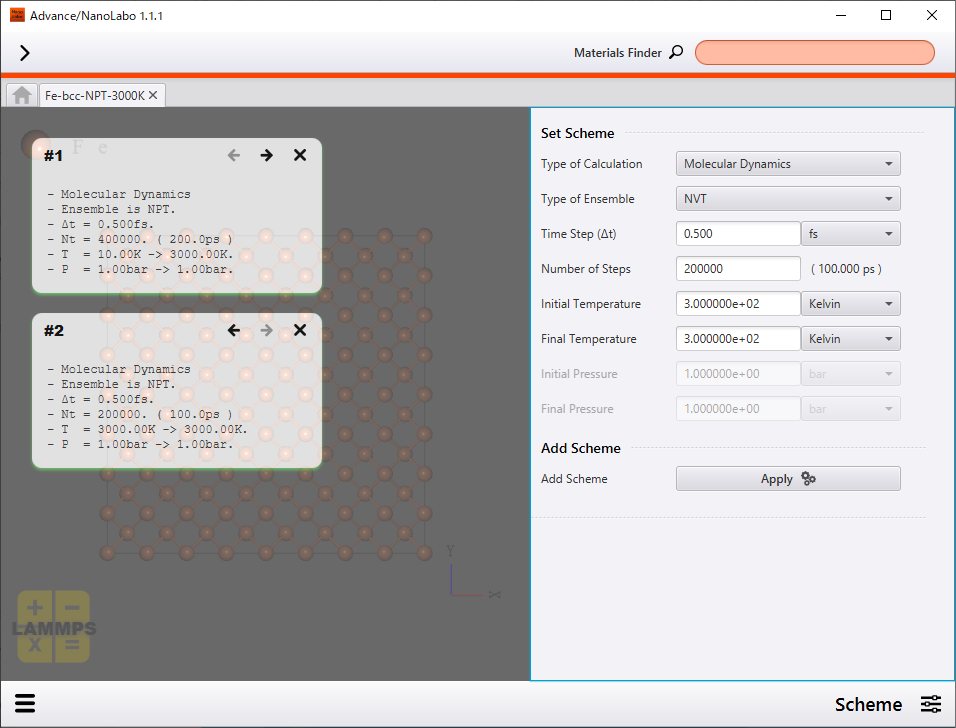
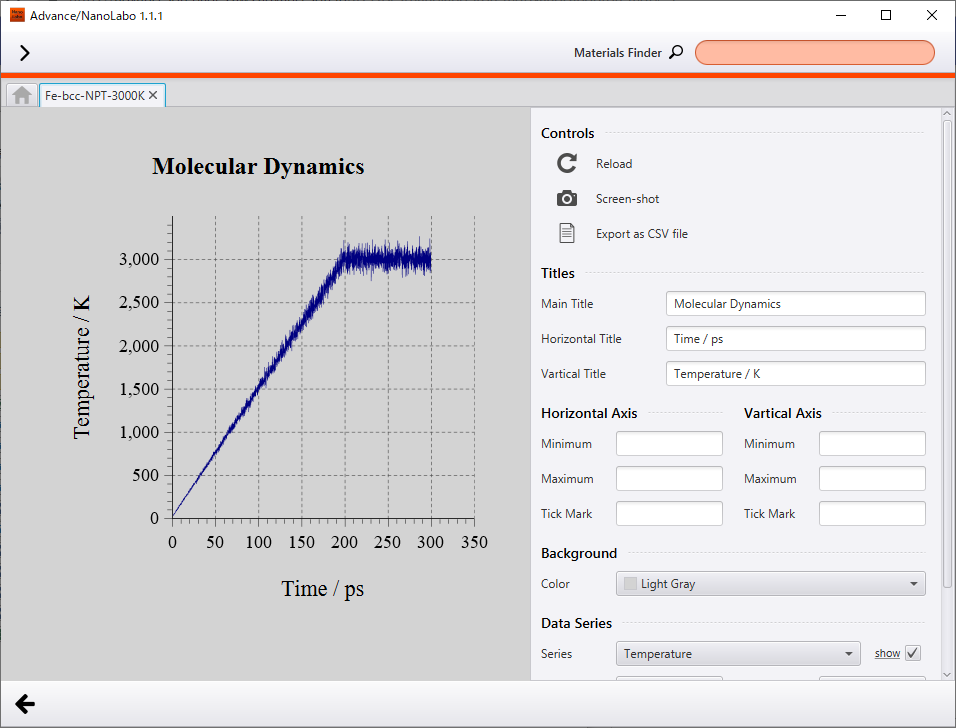
Finally, we show results of NPT simulation in which temperature was increased from 0 K to 3000 K at a constant rate in 200 ps and then kept 3000 K for 100 ps. On Advance/NanoLabo, different calculation schemes can be applied for a model in succession like this case.

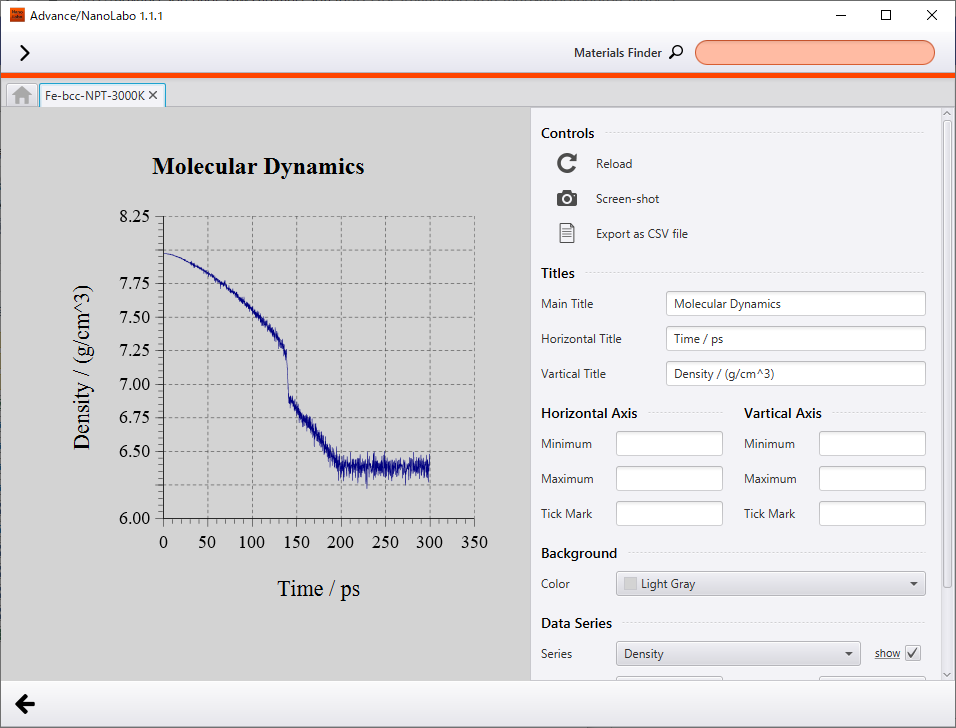
At the end of the simulation, temperature converged to 3000 K and density converged to 6.4 g/cm3. Over the simulation, the lattice expanded and density decreased as temperature increased. From the animation of crystal structure, we can see that atomic oscillation becomes intense along with increasing temperature, and finally the crystal structure breaks down.

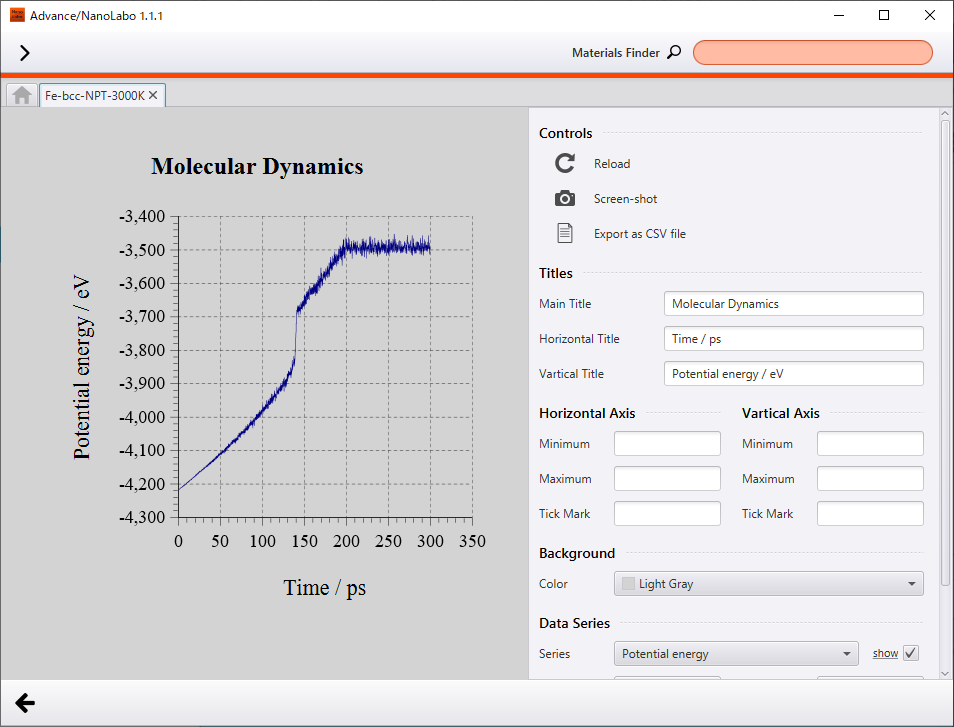
The most characteristic behavior of density is discontinuous change around 140 ps (about 2100 K), and we can find the same discontinuous behavior around 140 ps in plot of potential energy change. As compared to the animation of crystal structure, the discontinuous behavior corresponds to the breakdown of crystal structure with increasing atomic oscillation. We can interpret this as phase transition from solid phase to liquid phase. Besides, melting point of Fe reported experimentally is 1811 K3, and melting point of Fe obtained in the calculation is overestimated by about 300 K.

Setting of calculation scheme Change of temperature Change of density
Setting of calculation scheme
Change of temperature
Change of density
Change of potential energy
Change of potential energy
Animation of change of crystal structure

関連ページ#

  1. We used LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) as a solver of molecular dynamics simulation. LAMMPS is a calculation package for classical molecular dynamics simulation. LAMMPS can be applied on various systems such as solid and soft matter, and many application examples have been reported. Also, LAMMPS can execute parallel processing efficiently as the name suggests. ↩

  2. Nagakura, S., Inokuchi, H., Ezawa, H., Iwamura, H., Sato, F., Kubo R., ed.: "Iwanami Physicochemical Dictionary (the fifth edition)", Iwanami Shoten, Publishers (1998) Published in Japanese. ↩

  3. C. Kittel: "Introduction to Solid State Physics (the eighth edition) first volume and second volume", (Translated by UNO, R., TSUYA, N., Niizeki, K., Morita, A. and Yamashita, J.), Maruzen Publishing (2005) Published in Japanese. ↩