M3GNetを用いた熱膨張率の計算#
温度依存の物性に対するM3GNetの適用可能性を検討するために、 代表的な物質について融点以下の温度域で熱膨張率を計算した。
構造作成#
今回は全て立方晶の構造を用いた。 元となる構造はMaterials Projectのものを用いた。 また、ユニットセルでは自由度が低く、熱揺らぎによる体積変化が大きいため、 系全体で500原子程度になるように等方的にスーパーセルを構成した。 なお、以降述べる体積は全てユニットセルに換算したものである。
| Material | Al | Cu | Mg | MgO | NaCl | Si |
|---|---|---|---|---|---|---|
| Structure | mp-134 | mp-30 | mp-110 | mp-1265 | mp-22862 | mp-149 |
| Supercell | 5×5×5 | 5×5×5 | 6×6×6 | 4×4×4 | 4×4×4 | 4×4×4 |
| Tmelt (K) * | 933 | 1358 | 923 | 3125 | 1074 | 1683 |
| αV (10-6K-1) ** | 69 | 51 | 76 | 29 | 120 | 9 |
*融点 **体積膨張率(at 293 K)
分子動力学計算#
分子動力学計算はNPTアンサンブルで等方的なセル変形のみを許した。 各温度についてステップ幅1fsで10psまで10000ステップ計算を行った。 3ps以後について定常状態だと仮定し、平均を取ったものをその温度における体積とした。 さらに、不偏分散についても求め、各温度間で体積に有意差があることを確認した。
解析結果#
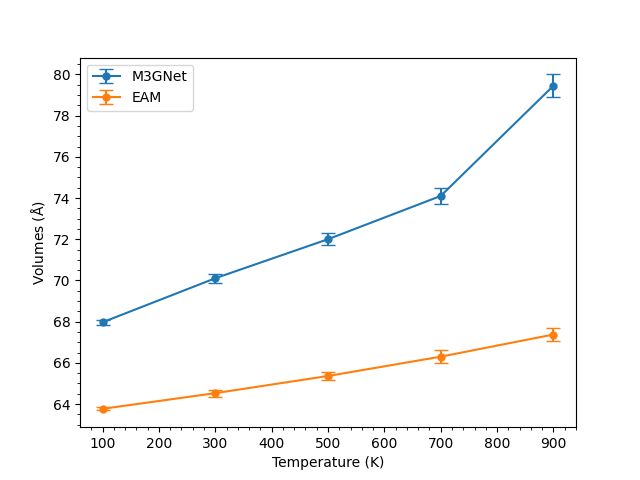
上図はAlについてM3GNetとEAMの両方の力場を用いて体積を比較した結果を示したものである。 M3GNetとEAMのどちらにおいても熱揺らぎによる体積のばらつきが十分小さく、熱膨張率の評価をすることができる。 また、M3GNetでは融点近傍で極端に体積が大きくなっており、このとき分子動力学計算後の結晶構造は完全に崩壊していた。
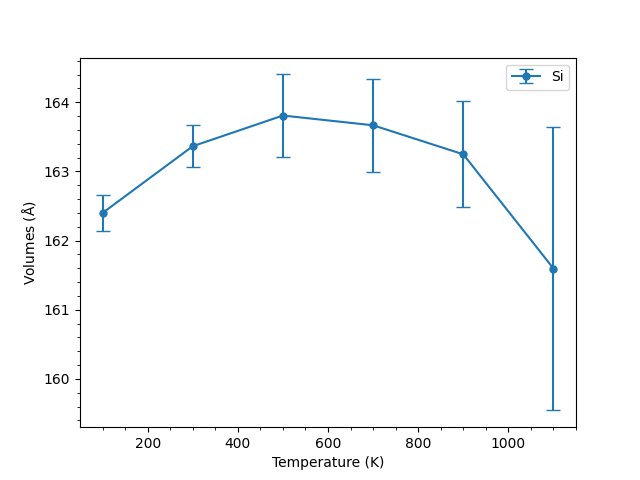
上図はSiについてM3GNetを用いた結果を示したものである。 500K程度から分散が大きくなり、1100Kでは結晶構造が大きく乱れていた。 Si以外の材料では全て体積のばらつきは十分に小さかったため、各材料の個別の図は省略する。
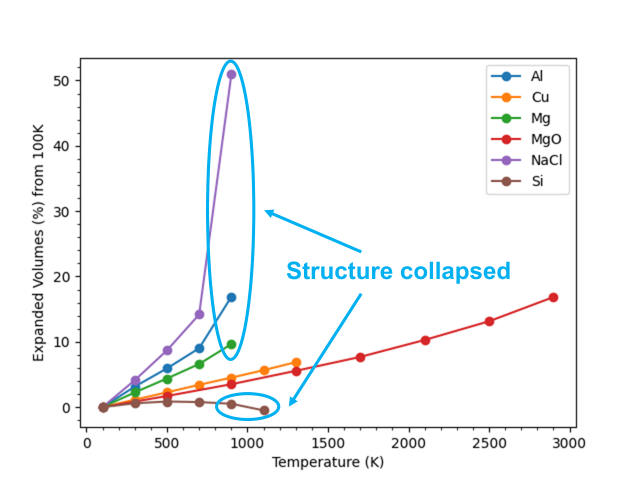
上図は各材料についてM3GNetを用いて、100Kを基準とした体積の変化率を示したものである。 分子動力学計算後の結晶構造が崩れていたデータ点は水色の線で囲われている。 結果として、結晶構造が崩れていない温度域においては、 どの材料の体積も温度に対してほぼ線形に増加することがわかった。 100Kと500Kの体積から体積膨張率を計算した結果を下の表にまとめた。
| Material | Al | Cu | Mg | MgO | NaCl | Si |
|---|---|---|---|---|---|---|
| αVREF (10-6K-1) | 69 | 51 | 76 | 29 | 120 | 9 |
| αVM3GNet (10-6K-1) | 148 | 57 | 110 | 43 | 217 | 22 |
EAMで計算したAlの体積膨張率は62.5 (10-6K-1)であり、文献値と近い値となった。 一方、M3GNetを用いた場合では、Alの体積膨張率は文献値の二倍以上の値となった。 M3GNetは第一原理計算の結果を学習させたNNPであり、高温の構造データを学習に用いていないので、 経験的なポテンシャルであるEAMの方が精度が高かった。 実際、多くの材料でM3GNetによる体積膨張率と文献値との間で乖離が見られた。
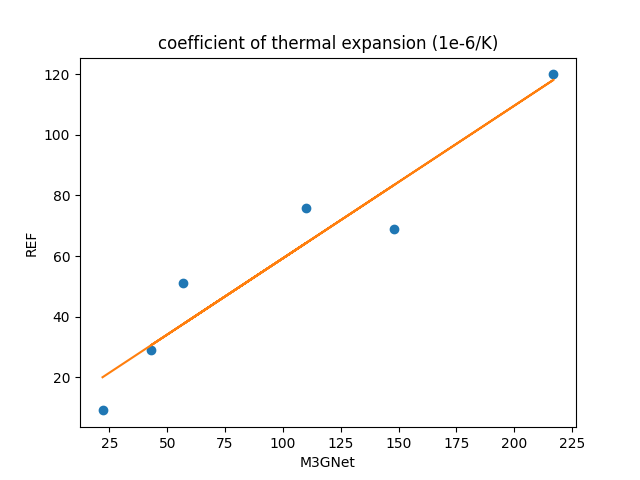
上図は横軸にM3GNetの体積膨張率、縦軸に文献値をプロットしたものである。 正の相関が見られたので、線形回帰を行った結果を以下の表に示した。 傾きが1から大きく乖離しており、分散も小さくないことから、M3GNetによる体積膨張率の評価は難しいことがわかる。
| a | b | s |
|---|---|---|
| 0.50 | 8.87 | 11.41 |
αVREF = a αVM3GNet + b (10-6/K)
s2: 不偏分散
まとめ#
様々な材料に対してM3GNetを用いて体積膨張率を評価した結果、 M3GNetによる予測は正の相関はあるものの精度が低いことがわかった。 これは、高温の構造を学習に用いていないことや、第一原理計算を教師としていることが原因として考えられた。 ただし、今回は第一原理分子動力学計算は今回は行わなかったため、原因を特定するまでには至らなかった。
以上のことから、M3GNetによる温度依存の物性の評価は難しいことがわかった。