Calculation of Coefficient of Thermal Expansion Using M3GNet#
To investigate the applicability of M3GNet to temperature dependent physical properties, the coefficient of thermal expansion for representative materials were calculated in the temperature range below the melting point.
Structure Creation#
In this study, cubic lattices were used for all materials. The original structures were from Materials Project. Since unit cells have low degrees of freedom and large volume changes due to thermal fluctuations, the supercells were isotropically configured so that the total number of atoms in the entire system was about 500. However, all volumes described below are converted to unit cells.
| Material | Al | Cu | Mg | MgO | NaCl | Si |
|---|---|---|---|---|---|---|
| Structure | mp-134 | mp-30 | mp-110 | mp-1265 | mp-22862 | mp-149 |
| Supercell | 5×5×5 | 5×5×5 | 6×6×6 | 4×4×4 | 4×4×4 | 4×4×4 |
| Tmelt (K) * | 933 | 1358 | 923 | 3125 | 1074 | 1683 |
| αV (10-6K-1) ** | 69 | 51 | 76 | 29 | 120 | 9 |
*melting point **volumetric expansion coefficient (at 293 K)
Molecular Dynamics Calculation#
Molecular dynamics calculations were performed in NPT ensemble allowing only isotropic cell deformation. For each temperature, calculations were performed in 10000 steps up to 10ps with a step width of 1fs. The volume after 3ps was assumed to be in a steady state, and the average volume was taken as the volume at that temperature. Besides, the unbiased dispersion was also calculated, and it was confirmed that there was a significant difference of volume at each temperature.
Analysis Result#
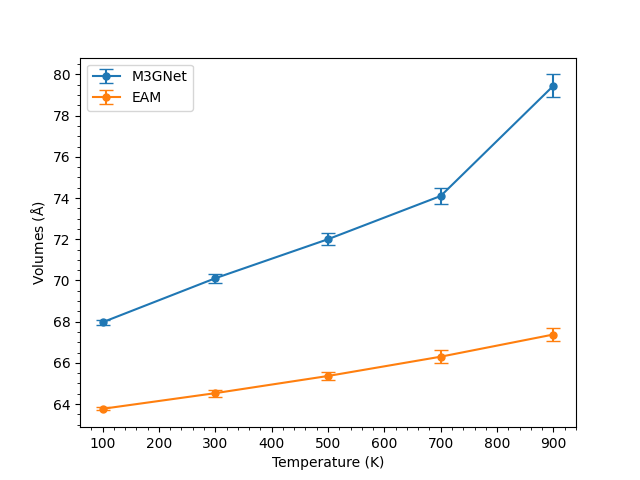
The above figure shows the results of volume comparisons for Al using both M3GNet and EAM force fields. In both M3GNet and EAM, the variation of volume due to thermal fluctuation was small enough to evaluate the coefficient of thermal expansion. As the volume calculated by M43GNet was extremely large near the melting point, the crystal lattice after molecular dynamics calculation was completely collapsed.
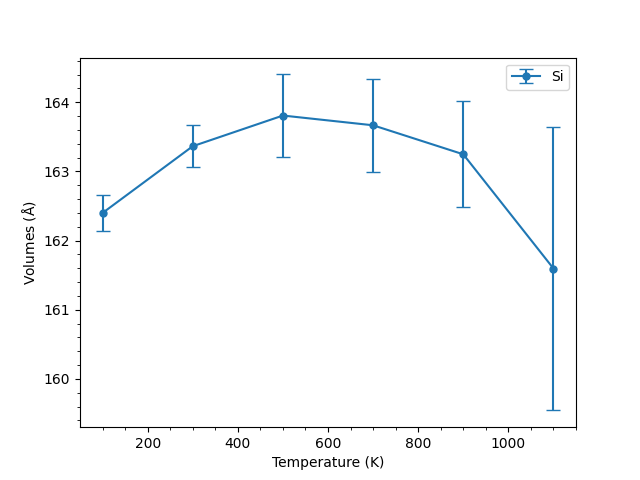
The above figure shows the results of M3GNet for Si. The dispersion increased from about 500 K, and the crystal structure was greatly disordered at 1100 K. Since the volume dispersion was sufficiently small for all materials except Si, individual figures for each material are omitted.
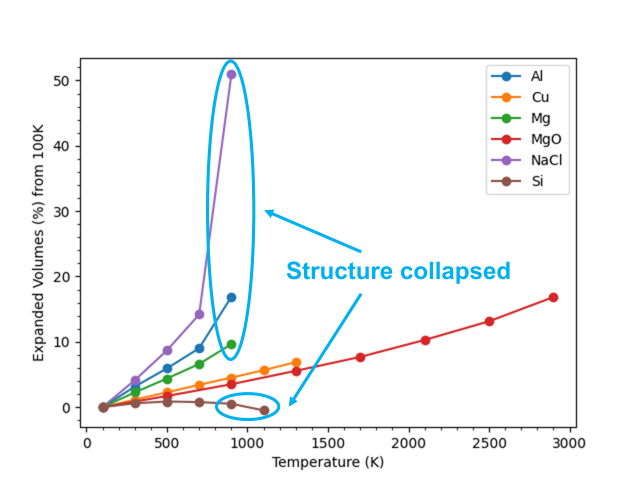
The above figure shows the rate of volume change with respect to the volume at 100 K for each material using M3GNet. The data points where the crystal lattice collapsed after molecular dynamics calculations are surrounded by light blue lines. The results showed that the volume of all materials increases almost linearly with temperature except where the crystal lattice was collapsed. The table below summarized the results of the volumetric expansion coefficients calculated from the volumes at 100 K and 500 K.
| Material | Al | Cu | Mg | MgO | NaCl | Si |
|---|---|---|---|---|---|---|
| αVREF (10-6K-1) | 69 | 51 | 76 | 29 | 120 | 9 |
| αVM3GNet (10-6K-1) | 148 | 57 | 110 | 43 | 217 | 22 |
The EAM calculated volumetric expansion coefficient of Al was 62.5 (10-6K-1), which is close to the literature value. On the other hand, the volume expansion coefficient of Al using M3GNet was more than twice the value in the literature. Since M3GNet is a NNP trained from first principles calculations and did not use high temperature structural data for training, the empirical potential, EAM was more accurate. In fact, there was a discrepancy between the volumetric expansion coefficient calculated by M3GNet and that of the literature values for many materials.
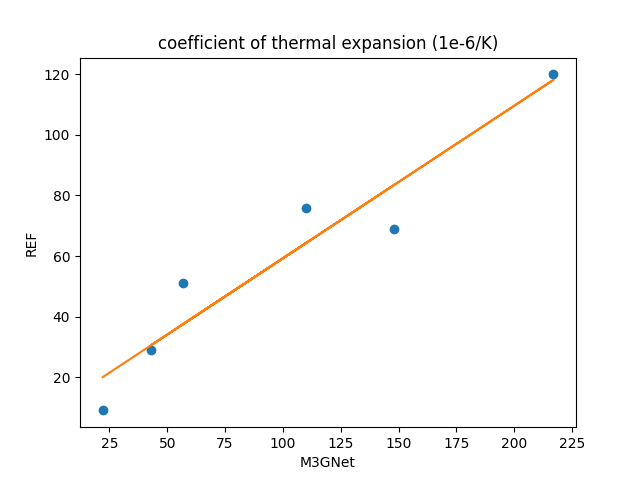
The above figure plots the volumetric expansion coefficient of M3GNet on the horizontal axis, and the literature values on the vertical axis. Since a positive correlation was observed, the results of a linear regression are shown in the following table. The slope deviates significantly from 1 and the variance was not small, indicating that it is difficult to evaluate the volumetric expansion coefficient using M3GNet.
| a | b | s |
|---|---|---|
| 0.50 | 8.87 | 11.41 |
αVREF = a αVM3GNet + b (10-6/K)
s2: unbiased dispersion
Summary#
The results of evaluating volumetric expansion coefficients using M3GNet for a variety of materials showed that the predictions with M3GNet were inaccurate, although there was a positive correlation. This may be due to the fact that high temperature structures were not used for training. Alternatively, first principles calculation itself may not reproduce volume expansion coefficients. Note that the critical reason cannot be determined since first principles molecular dynamics calculations were not performed.
From the above, it was found that it is difficult to evaluate temperature dependent properties using M3GNet.