M3GNetを用いた正極材料MoS₂/Ti₂CT₂(T=F,O)二層膜の機械特性の計算#

ナノ材料統合GUI Advance/NanoLaboでは、汎用グラフニューラルネットワーク力場M3GNet¹を用いた分子動力学シミュレーション²を実行することができます。本事例では、M3GNetを用いた分子動力学シミュレーションを行い、 $\text{Li/Na}$ イオン電池のフレキシブルな正極材料としての応用が期待される $\text{MoS}_2\text{/Ti}_{2}\text{CT}_2\text{(T=F,O)}$ 二層膜³の機械特性を調べました。

汎用グラフニューラルネットワーク力場M3GNet#

M3GNetは、Materials Project⁴の膨大なDFTによる構造緩和データを学習した、3体相互作用を伴う汎用グラフニューラルネットワーク力場です。M3GNetを用いることで、物質ごとに力場パラメータの最適化をすることなく、分子動力学計算を短時間で精度よく実行できることが期待されます。また、Advance/NanoLaboではM3GNetにSimple DFT-D3⁵による補正を加えて、van der Waals力についても考慮したシミュレーションを行うことが可能です。本事例では、二層間のvan der Waals相互作用を考慮するためにSimple DFT-D3による補正を加えてシミュレーションを行いました。

正極材料MoS₂/Ti₂CT₂(T=F,O)二層膜#

近年では、ウェアラブルな電子機器への応用に向けてフレキシブルな電極材料の開発が必要とされています。そのような中で、2次元正極材料として知られている $\text{MoS}_2$ や $\text{Ti}_{2}\text{CT}_2\text{(T=F,O)}$ の機械特性・電気特性が、複合構造をとることで向上するという報告がされています³。本事例では、M3GNetを用いた分子動力学計算により、これらの材料の機械特性の計算・比較を行いました。

計算モデルの作成#

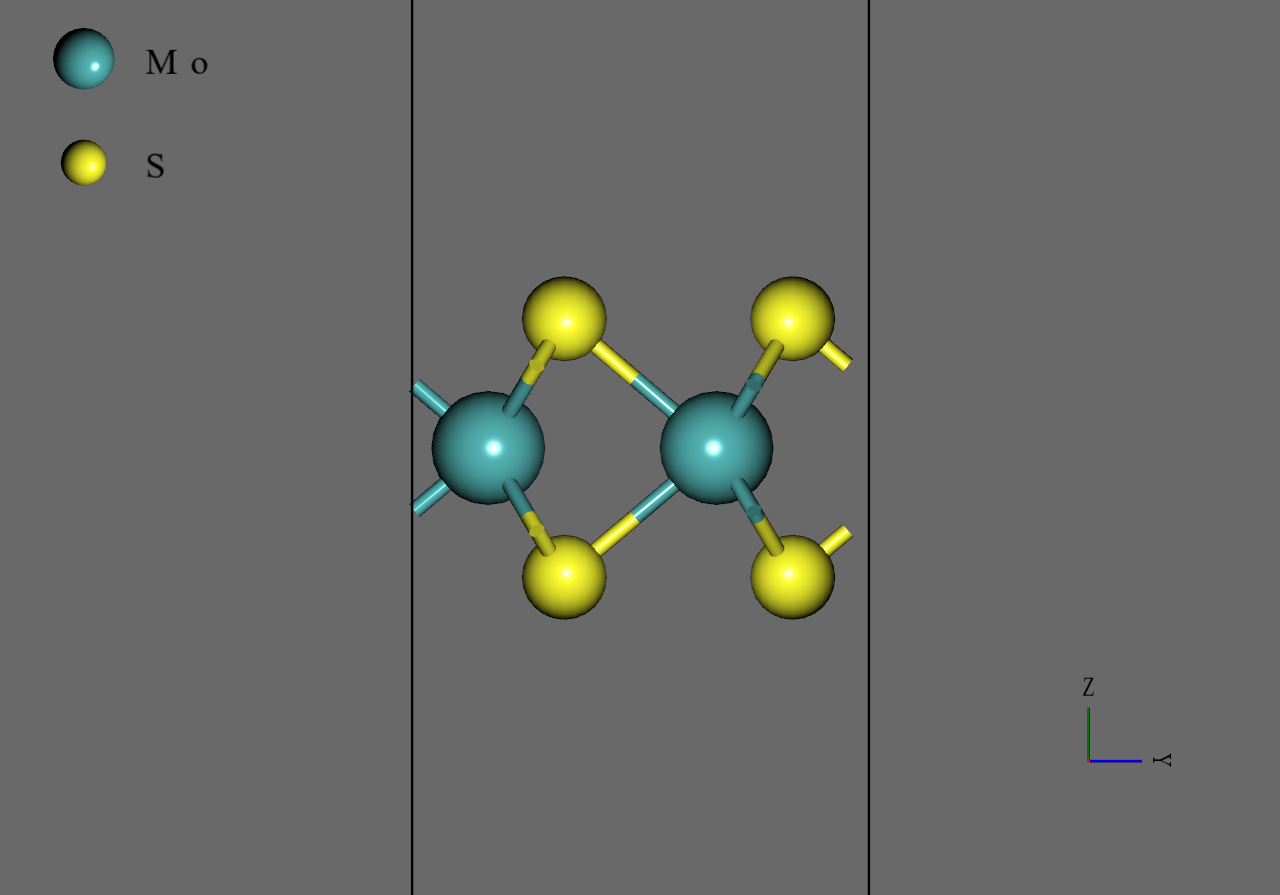
$\text{MoS}_2$ のモデル構造は、Materials Projectより取得した $\text{MoS}_2$ の構造ファイル(mp-2815)をもとに作成しました。まず、mp-2815に含まれる二層のうちの一層を削除しました。次に、セル形状を直方晶系に変換し、さらに $2×1×1$ のスーパーセルモデルを作成しました。最後に、anisotropicな変形を許して、 $0 \text{ bar}$ のもとで構造最適化を行いました。なお、これ以降のすべてのシミュレーションにおいて、時間の刻み幅は $1 \text{ fs}$ とし、力場にはSimple DFT-D3による補正を加えたM3GNetを用いました。

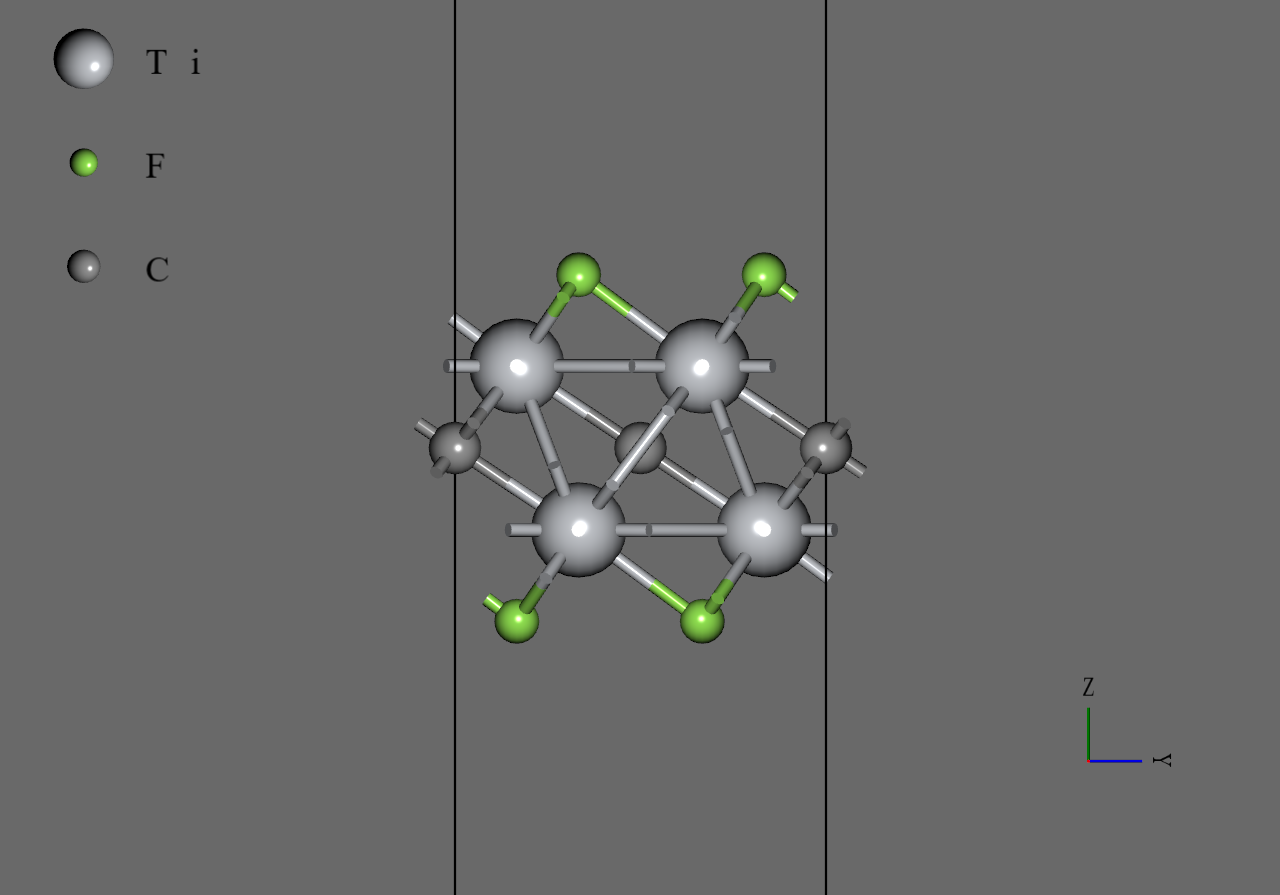
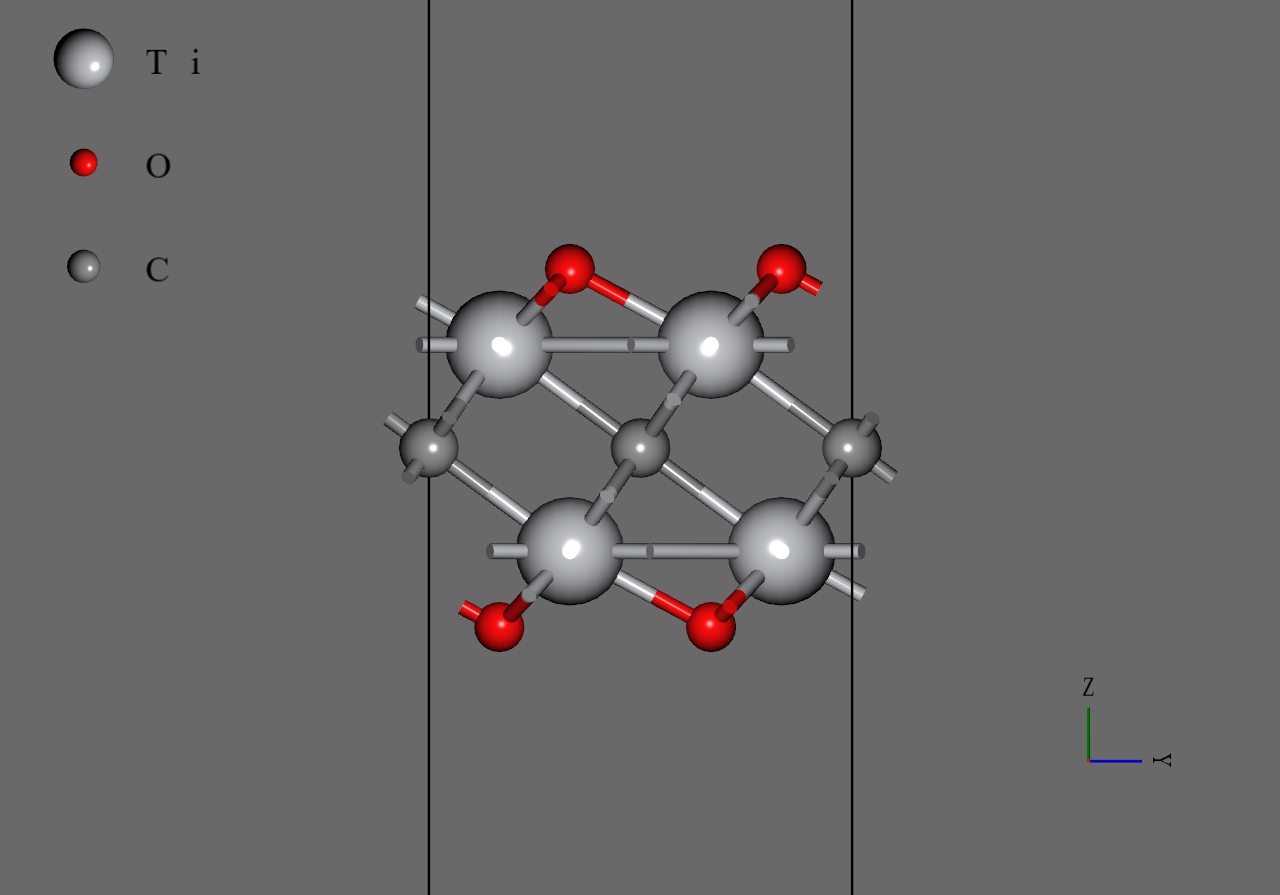
$\text{Ti}_{2}\text{CT}_2\text{(T=F,O)}$ のモデル構造は、Materials Projectより取得した $\text{Ti}_{2}\text{CAl}$ の構造ファイル(mp-12990)をもとに作成しました⁶。まず、mp-12990に含まれる2つの $\text{Ti}$ 原子及び1つの $\text{C}$ 原子を削除し、 $\text{Ti}_{2}\text{CAl}_2$ の単層構造を作成しました。次に、 $\text{Al}$ 原子を $\text{F}$ 原子または $\text{O}$ 原子に置換し、それらの原子の $z$ 座標を適当な値に調整しました。その後、セル形状を直方晶系に変換し、 $2×1×1$ のスーパーセルモデルを作成しました。最後に、anisotropicな変形を許して、 $0 \text{ bar}$ のもとで構造最適化を行いました。

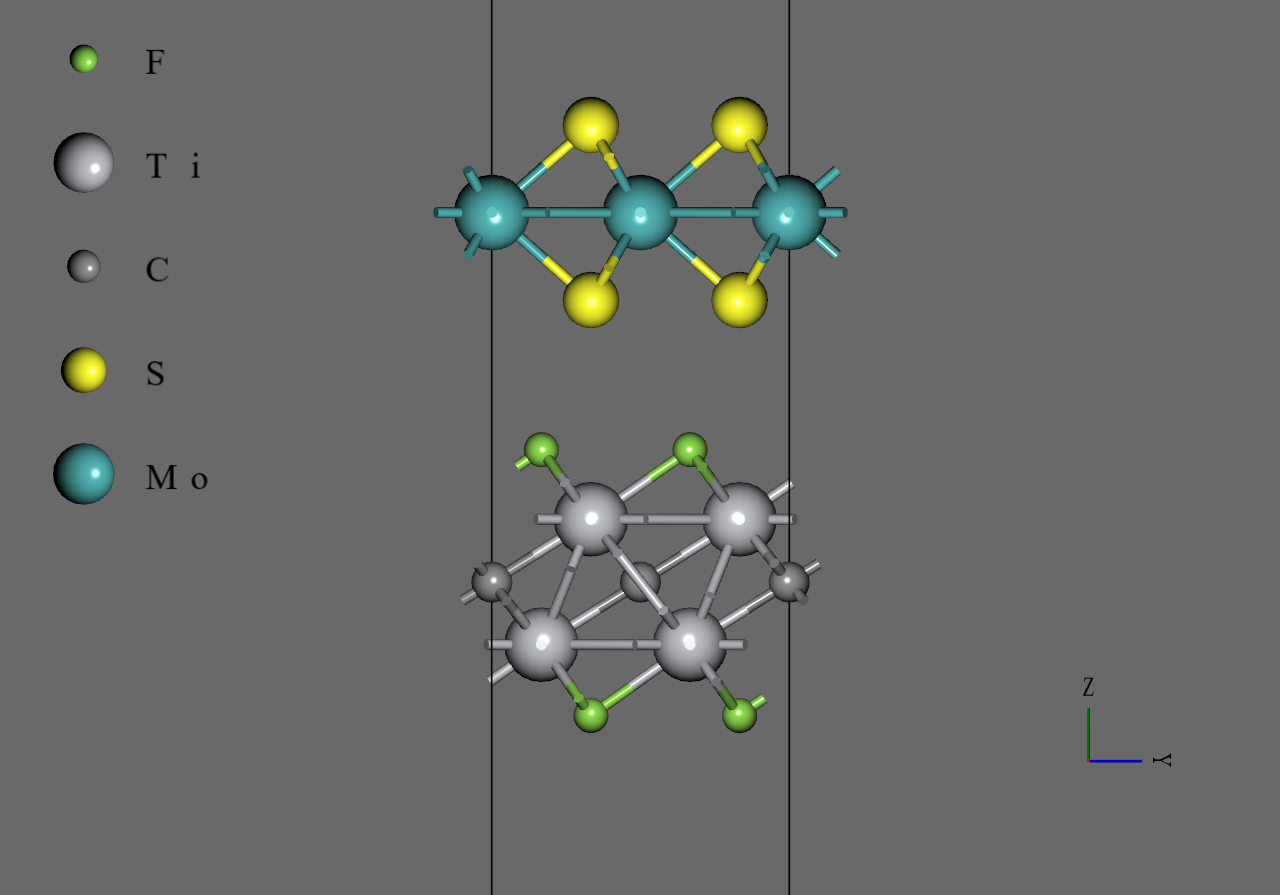
$\text{MoS}_2\text{/Ti}_{2}\text{CT}_2\text{(T=F,O)}$ 二層膜のモデル構造は、以上で作成したそれぞれのモデルをもとに、Advance/NanoLaboの界面ビルダーによって作成しました。格子定数は二種類の材料の中間の値とし、積層パターンは先行研究³におけるatop-1構造、hcp-1構造を $\text{MoS}_2\text{/Ti}_{2}\text{CF}_2$ 、 $\text{MoS}_2\text{/Ti}_{2}\text{CO}_{2}$ のそれぞれに適用しました⁷。また、モデラー機能により層間距離を適当な値に調節しました。最後に、anisotropicな変形を許して、 $0 \text{ bar}$ のもとで構造最適化を行いました。

なお、すべてのモデルにおいて、真空層の厚さを十分にとるために膜厚方向のセルの長さを30 Å程度としました。

Advance/NanoLaboでは、GUIによりこれらのような種々の構造を容易に作成することができます。


MoS₂	Ti₂CF₂	Ti₂CO₂

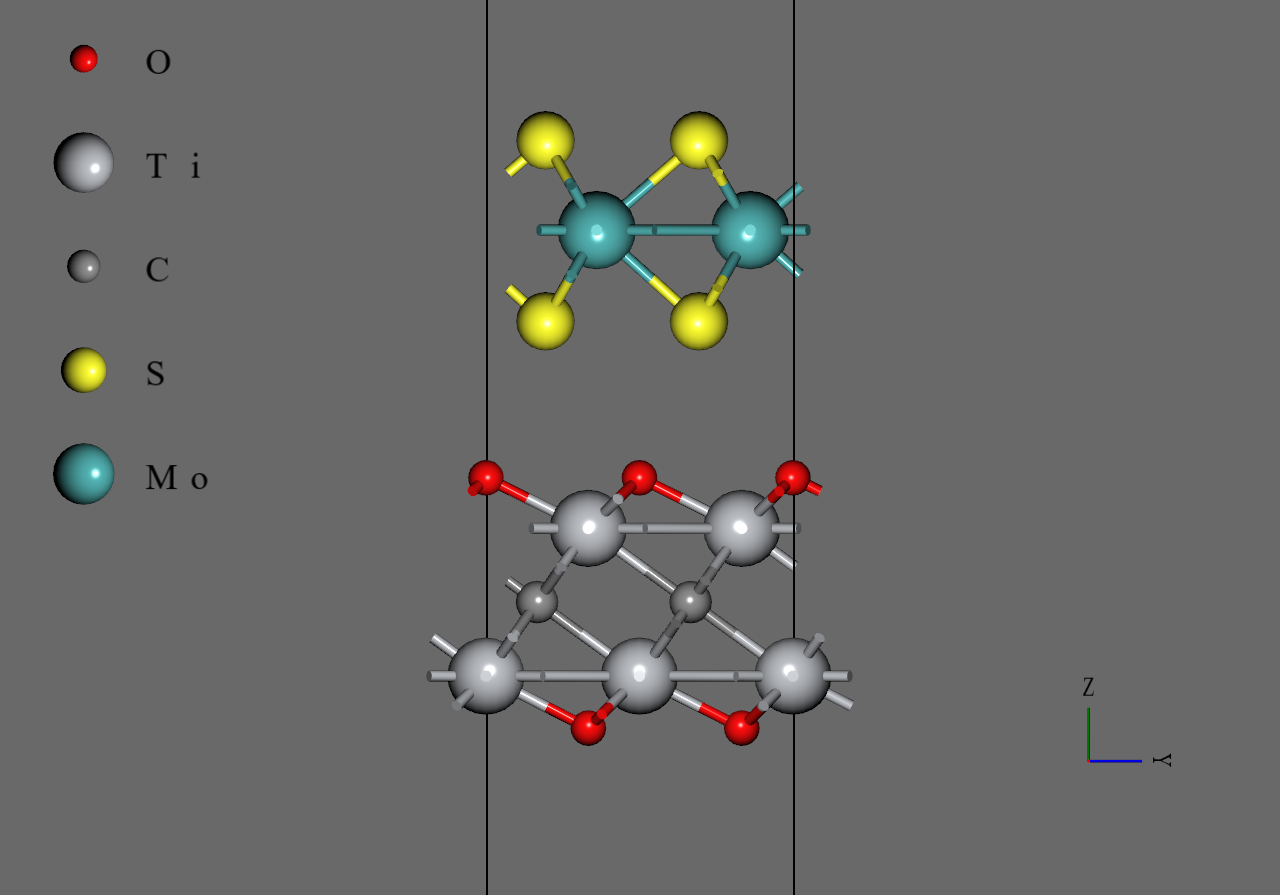
MoS₂/Ti₂CF₂	MoS₂/Ti₂CO₂

計算スキームの設定#

以上のようにして作成したそれぞれのモデルについて、構造最適化と $x$ 方向へのセルの変形を交互に繰り返しながら、 $x,y$ 方向に生じる応力とひずみの関係を調べました。なお、本事例ではすべてのモデルにおいて $x$ 方向はハニカム構造のzigzag方向に対応しています。

このとき、構造最適化はセルの変形を許さずに行いました。また、構造最適化が終了するごとに加えるひずみの大きさは0.002とし、初期構造からのひずみが0.2となるまで計算を繰り返しました。

以上のような計算スキームは、Advance/NanoLabo上で直接input fileを編集することで設定できます。

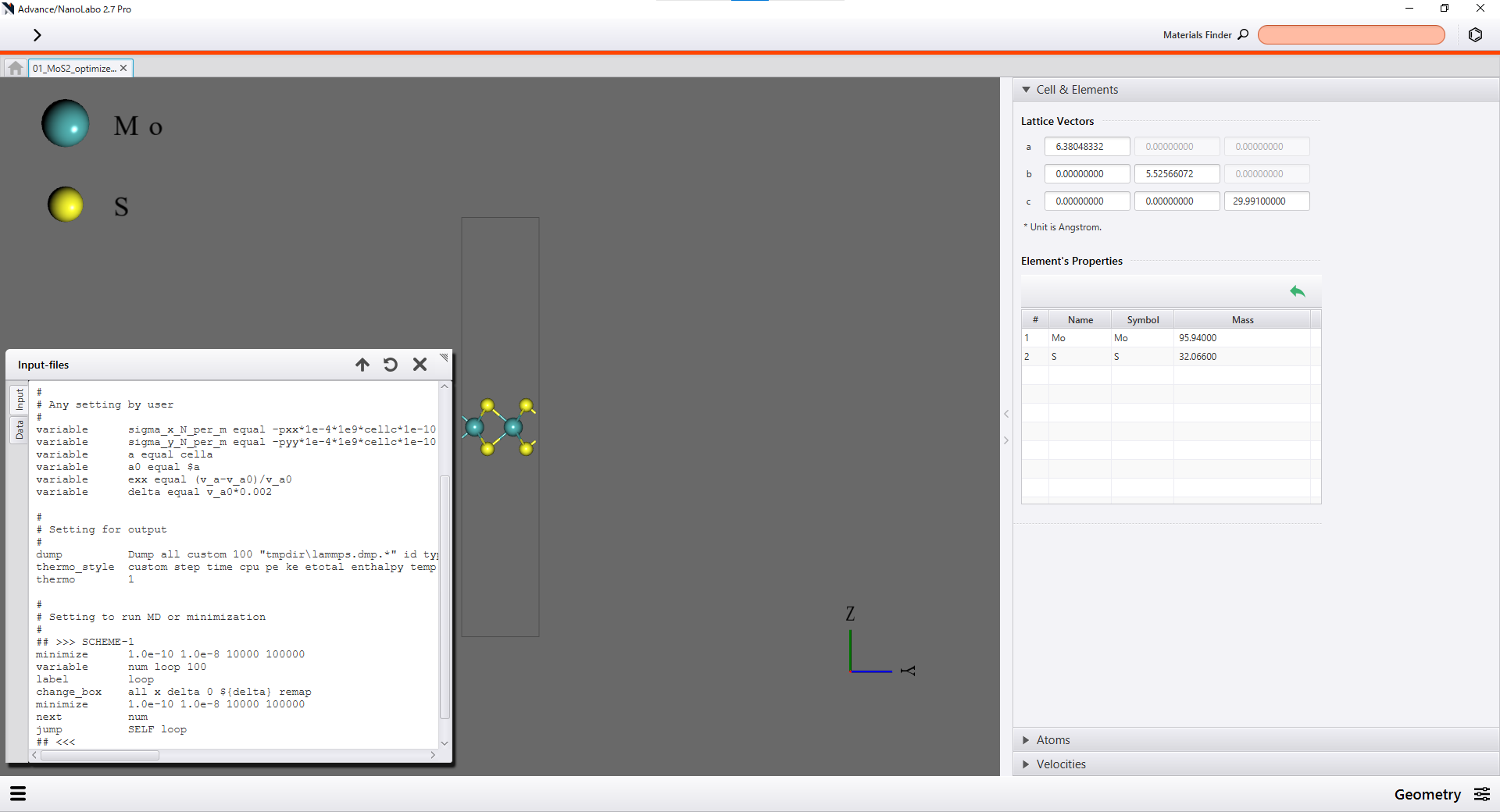
GUI上でのinput fileの編集

計算結果#

以上のシミュレーションで得られた、各モデル構造におけるひずみ $\epsilon_x$ と応力 $\sigma_x,\sigma_y$ の関係を下図に示します。

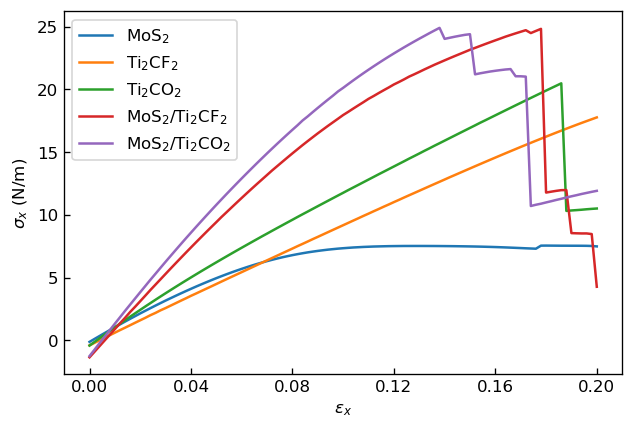
ひずみε_xと応力σ_xの関係

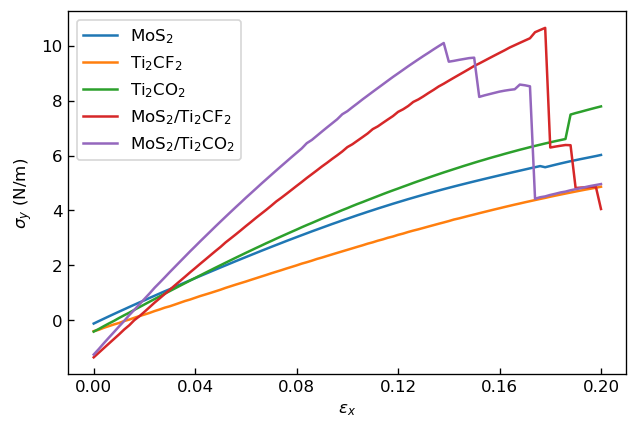
ひずみε_xと応力σ_yの関係

2次元系の場合、せん断応力を無視すると、応力 $\sigma$ とひずみ $\epsilon$ は次の関係にあります。

$\left( \begin{matrix} \sigma_x \\ \sigma_y \end{matrix} \right) = \left( \begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right) \left( \begin{matrix} \epsilon_x \\ \epsilon_y \end{matrix} \right)$

ここで、 $C_{ij}(i,j=1\text{ or }2)$ は弾性定数であり、弾性定数テンソルの対称性から $C_{12}=C_{21}$ が成り立ちます。また、本事例で扱っている系はすべて六方晶系であるため、その対称性から $C_{11}=C_{22}$ の関係も成立します⁸。

特に、 $x$ 方向にのみひずみを加えた場合( $\epsilon_y=0$ )には次の関係が成り立ちます。

$\sigma_x = C_{11}\epsilon_x$ $\sigma_y = C_{12}\epsilon_x$

この関係を用いると、応力-ひずみ曲線の線形領域を1次関数でフィッテイングしたときの傾きが弾性定数に相当することがわかります。本事例では、ひずみが0~0.02の範囲でフィッテイングを行い、弾性定数 $C_{11}$ , $C_{12}$ を算出しました。先行研究³においてDFT計算により求められた弾性定数を横軸に、本事例でM3GNetにより求めた弾性定数を縦軸にプロットした図を以下に示します。

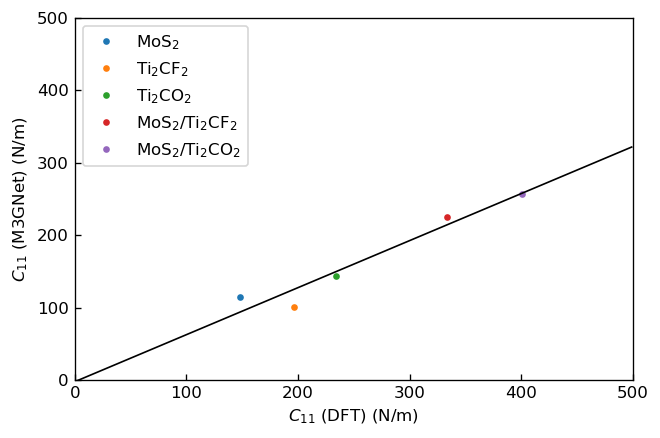
DFTおよびM3GNetにより求めたC₁₁の相関

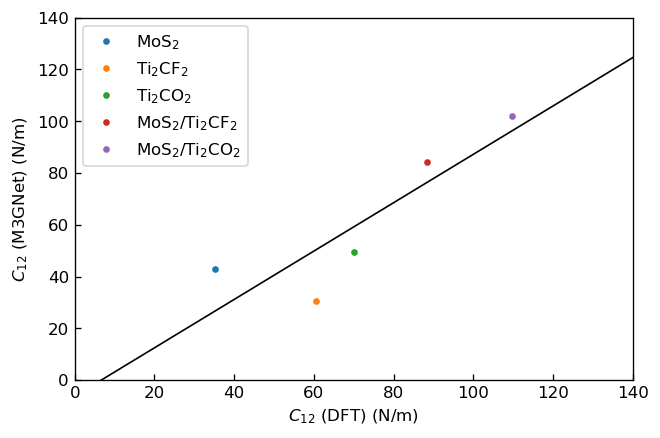
DFTおよびM3GNetにより求めたC₁₂の相関

これらのプロットを1次関数でフィッテングした際の傾き及び切片を以下に示します。

	傾き	切片
C₁₁	0.65	-2
C₁₂	0.9	-6

いずれの弾性定数についてもDFTの結果とM3GNetの結果との間に正の相関がみられますが、DFTに比べてM3GNetは弾性定数を過少評価する傾向にあることがわかります。

また、これらの弾性定数および次式³を用いて、それぞれの系における面内方向のヤング率 $E$ 及びポアソン比 $\nu$ を算出しました。 $E = (C_{11}^2-C_{12}^2)/C_{11}$ $\nu = C_{12}/C_{11}$

先行研究においてDFT計算により求められたヤング率、ポアソン比を横軸に、本事例でM3GNetにより求めたヤング率、ポアソン比を縦軸にプロットした図をそれぞれ以下に示します。

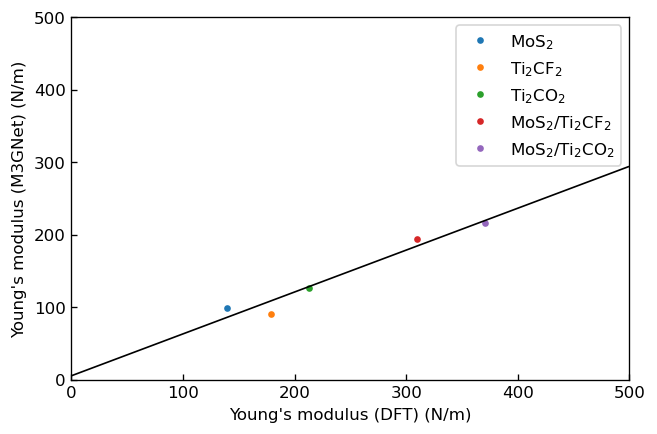
DFTおよびM3GNetにより求めたヤング率Eの相関

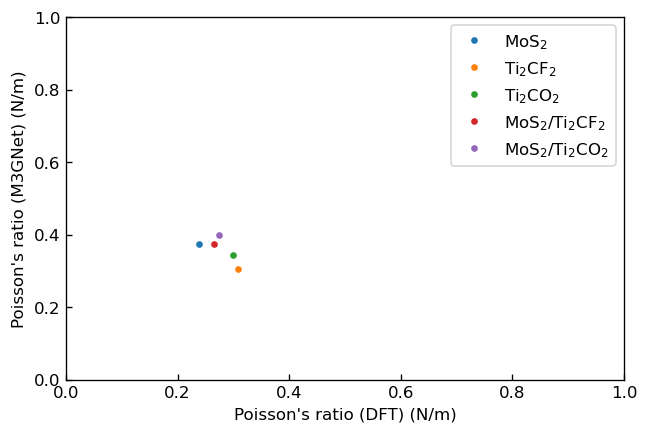
DFTおよびM3GNetにより求めたポアソン比νの相関

これらのプロットを1次関数でフィッテングした際の傾き及び切片を以下に示します。

	傾き	切片
E	0.58	5
ν	-0.9	0.6

ヤング率 $E$ においては、弾性定数の場合と同様に、正の相関がみられるもののM3GNetの結果は過少評価となっていることがわかります。一方、ポアソン比 $\nu$ においては正の相関は見られませんが、M3GNetを用いた計算でもDFTの結果と同程度のオーダーの値の見積もりは可能であることがわかります。また、いずれの系も複合構造をとることでヤング率が向上するという、DFTの場合と同様の結果を得ることができました。

本事例のシミュレーションにかかった時間は、一つの系当たり最大で15分程度(OpenMP 20スレッド並列で計算)であり、DFT計算に比べて大幅に計算コストが削減されています。また、M3GNetは主にバルク構造をもとに学習した汎用力場ですが、本事例で扱ったような2次元系でも、DFTの結果との間に正の相関をもつ弾性定数を算出することができました。

M3GNetを用いた正極材料MoS2/Ti2CT2(T=F,O)二層膜の機械特性の計算#