Calculation of mechanical properties of MoS₂/Ti₂CT₂ (T=F,O) bilayers using M3GNet#

On Advance/NanoLabo, an integrated GUI for nanomaterials, you can execute molecular dynamics simulation¹ with M3GNet², a general force field based on graph neural networks.

We introduce calculation of mechanical properties of $\text{MoS}_2\text{/Ti}_{2}\text{CT}_2\text{ (T=F,O)}$ bilayers³, promising flexible anode materials for $\text{Li/Na}$ ion batteries, via molecular dynamics simulation with M3GNet.

M3GNet, a general force field based on graph neural networks#

M3GNet is a universal interatomic potential based on graph neural networks with three-body interactions which was trained on the enormous DFT data of structural relaxation recorded in Materials Project⁴. M3GNet will enable you to execute molecular dynamics simulation with low computational cost, good accuracy and no need to parametrize force fields for each compound.

On Advance/NanoLabo, you can add Simple DFT-D3⁵ correction to M3GNet to consider van der Waals force during molecular dynamics simulation. We calculated van der Waals interaction at the interface of the two layers of $\text{MoS}_2\text{/Ti}_{2}\text{CT}_2\text{ (T=F,O)}$ bilayers using Simple DFT-D3 correction.

MoS₂/Ti₂CT₂ (T=F,O) bilayers#

Searching for flexible electrode materials is needed more and more for wearable electronics applications. Recently, it has been reported that forming heterostructures of $\text{MoS}_2$ and $\text{Ti}_{2}\text{CT}_2\text{ (T=F,O)}$ , which are known as two-dimensional anode materials, improve mechanical and electronic properties of those³.

We calculated mechanical properties of these materials via molecular dynamics simulation with M3GNet.

Generation of calculation models#

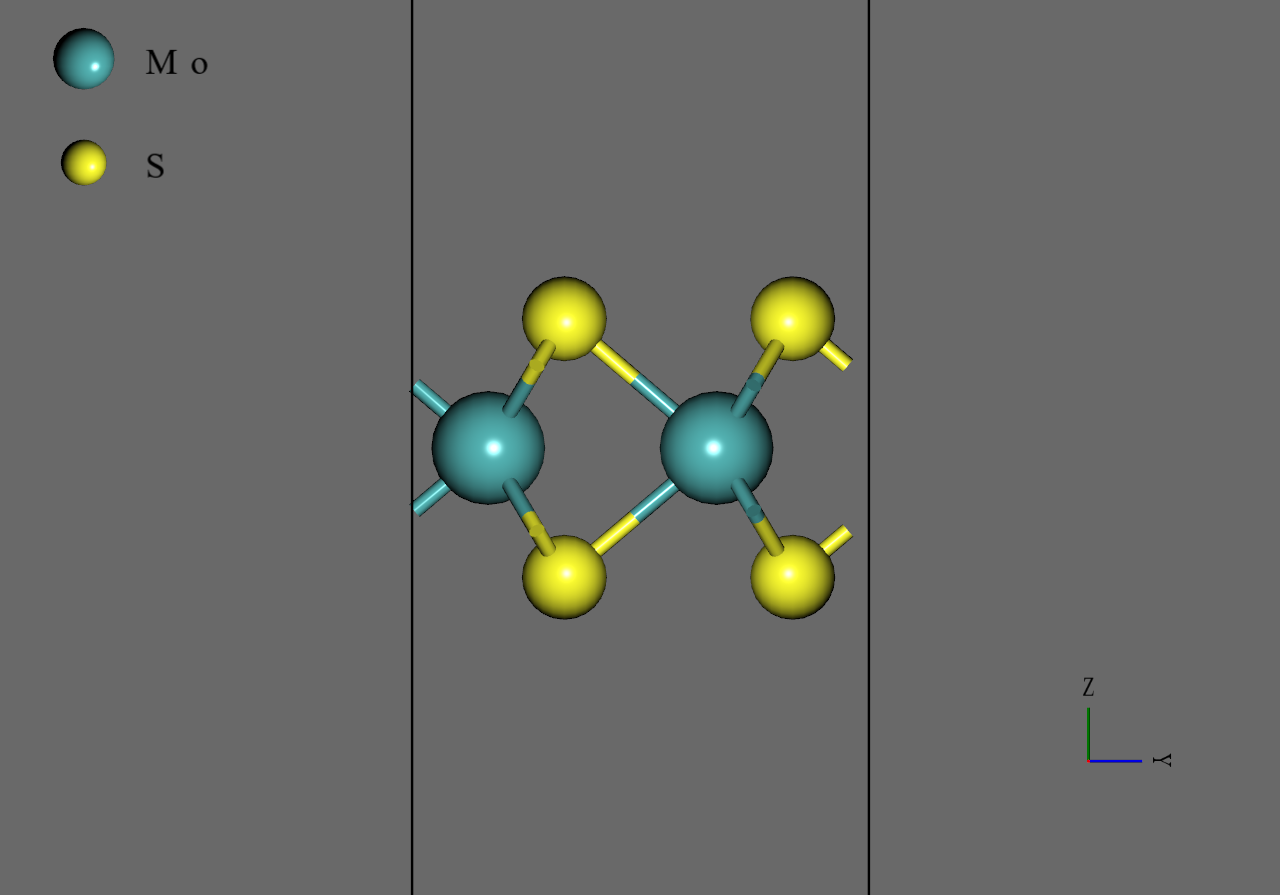
We generated model structure of $\text{MoS}_2$ from mp-2815, the structure file of $\text{MoS}_2$ downloaded from Materials Project. Firstly, we removed one layer of the bilayer of mp-2815. Secondly, we converted the cell to orthorhombic and generated $2×1×1$ supercell model. Finally, we performed structural optimization under $0 \text{ bar}$ allowing cell to change anisotropically. We note that we used M3GNet as force filed with Simple DFT-D3 correction and simulation time step was $1 \text{ fs}$ for all simulations.

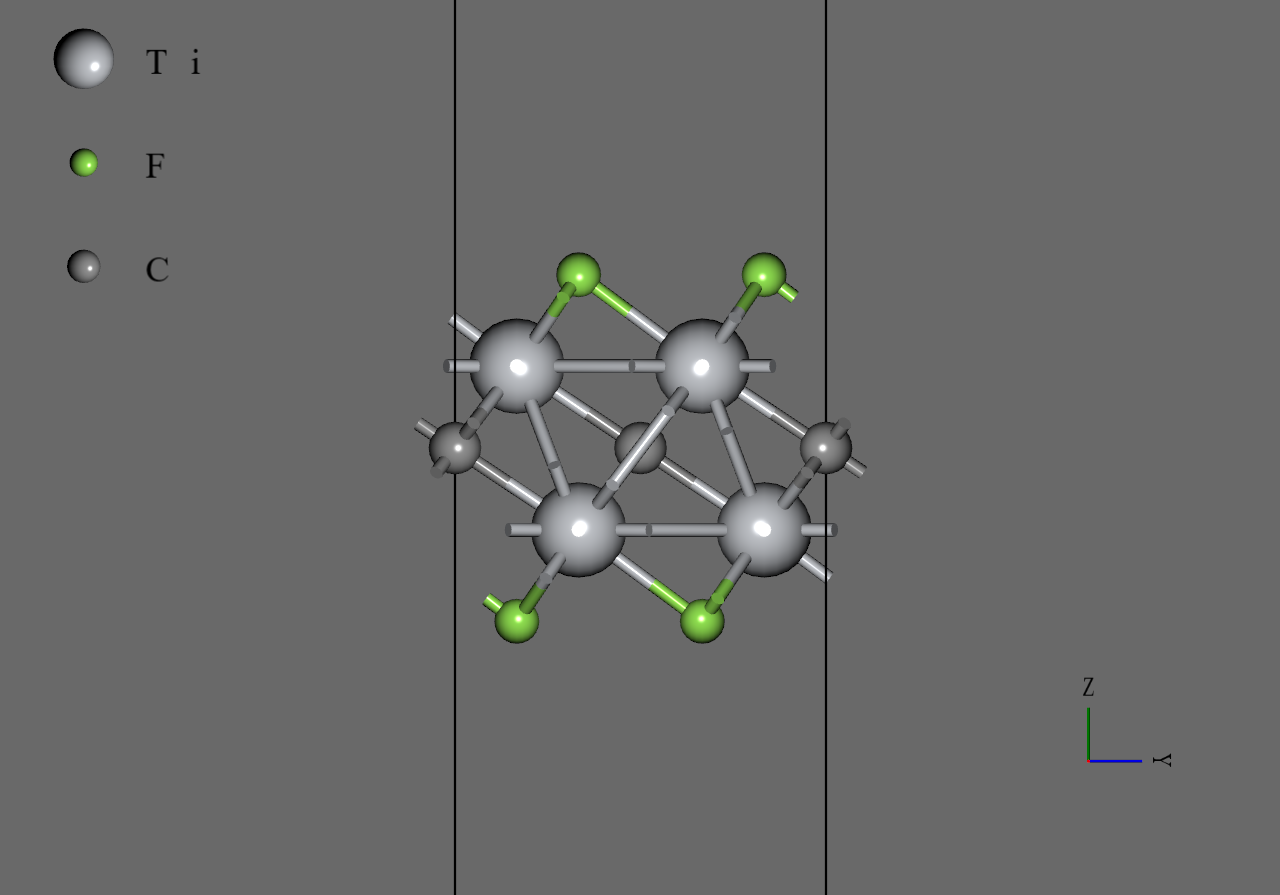
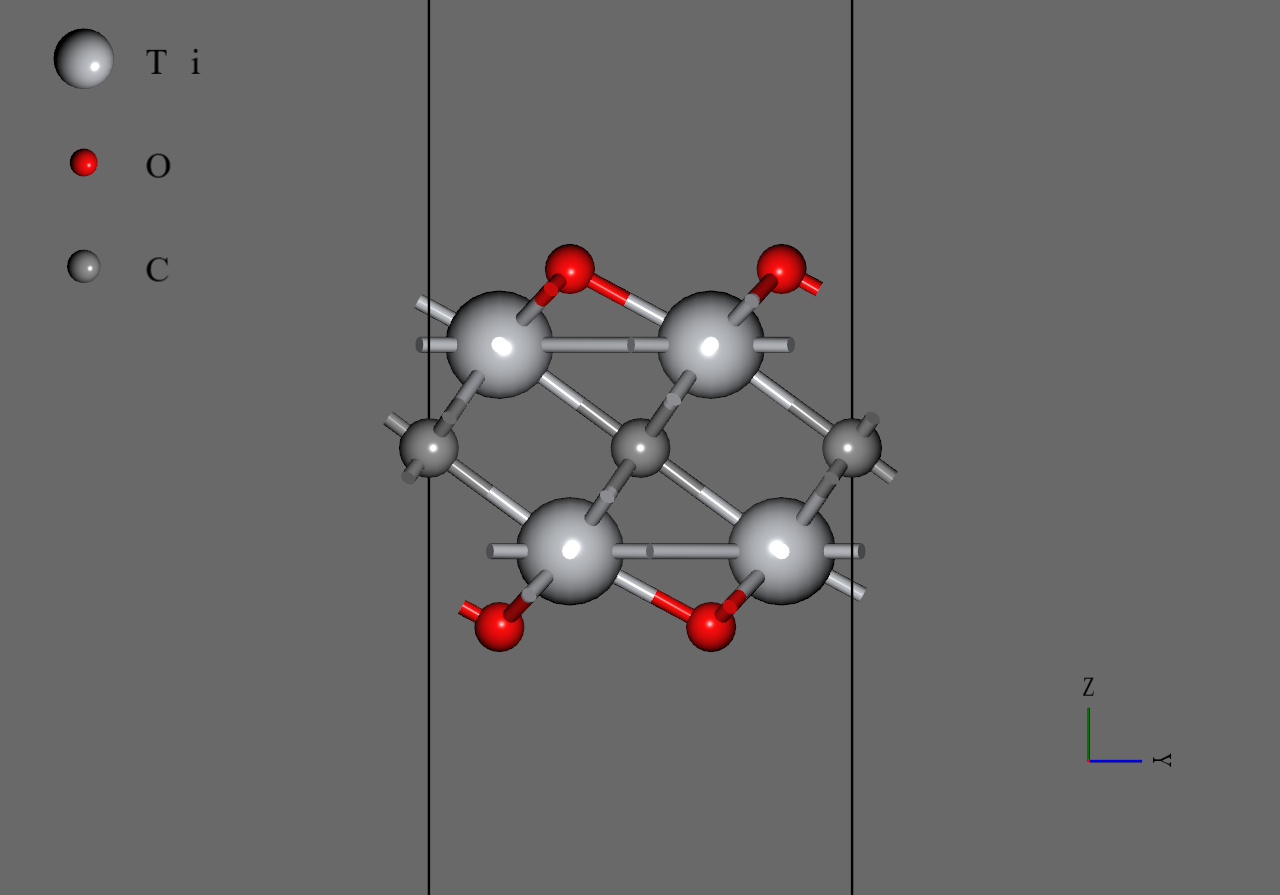
We generated model structures of $\text{Ti}_{2}\text{CT}_2\text{ (T=F,O)}$ from mp-12990, the structure file of $\text{Ti}_{2}\text{CAl}$ ⁶ downloaded from Materials Project. Firstly, we removed two $\text{Ti}$ atoms and a $\text{C}$ atom of mp-12990 to generate monolayer of $\text{Ti}_{2}\text{CAl}_2$ . Secondly, we replaced $\text{Al}$ atoms with $\text{F}$ atoms or $\text{O}$ atoms and adjusted $z$ positions of the replaced atoms roughly. Then, we converted the cell to orthorhombic and generated $2×1×1$ supercell model. Finally, we performed structural optimization under $0 \text{ bar}$ allowing cell to change anisotropically.

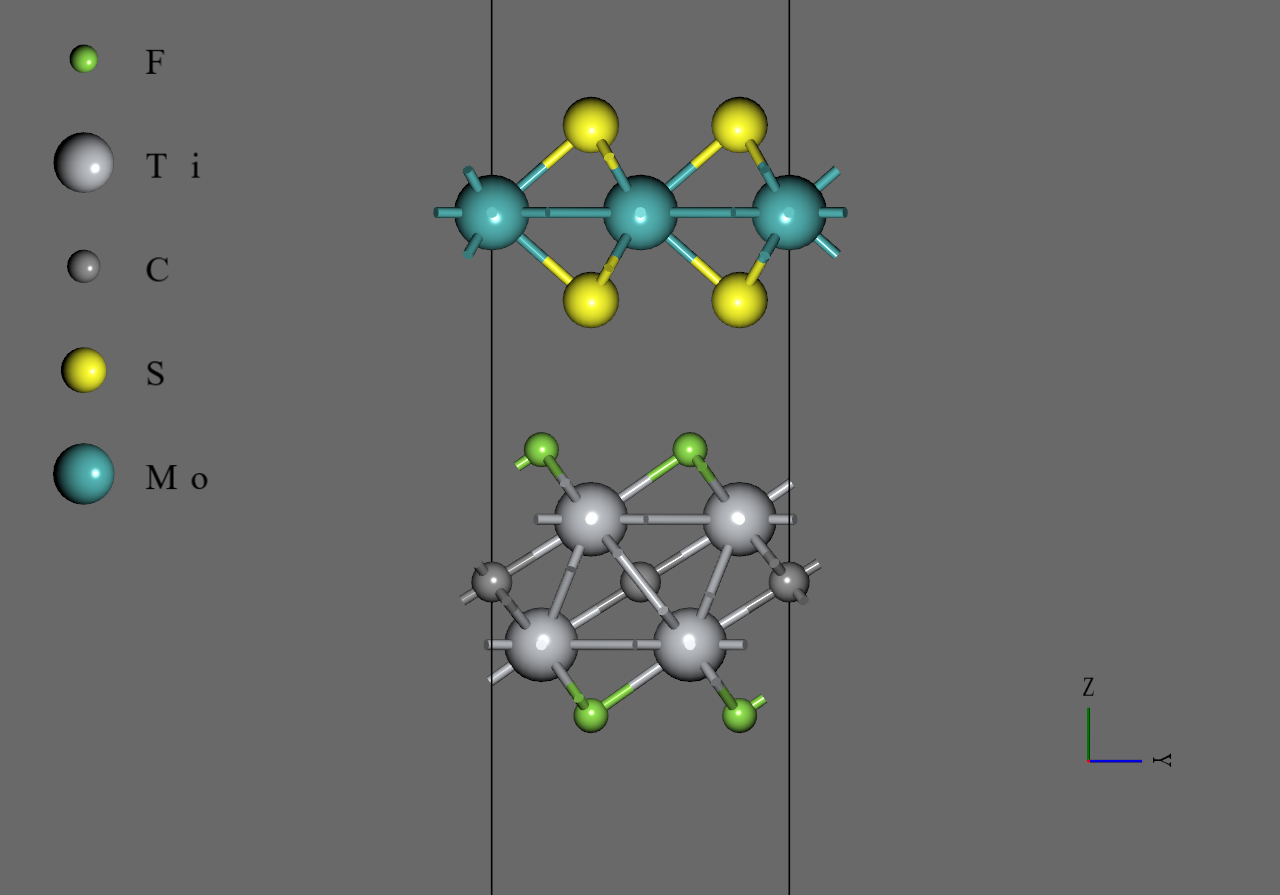
We generated model structures of $\text{MoS}_2\text{/Ti}_{2}\text{CT}_2\text{ (T=F,O)}$ bilayers from the monolayer models using interface builder function of Advance/NanoLabo. The lattice constant of the bilayer is set as the average of that of the two monolayers. In regard to the stacking patterns, atop-1³ configuration was adopted for $\text{MoS}_2\text{/Ti}_{2}\text{CF}_2$ , and hcp-1³ configuration was adopted for $\text{MoS}_2\text{/Ti}_{2}\text{CO}_{2}$ ⁷. Also, we adjusted interlayer distance using modeler function of Advance/NanoLabo. Finally, we performed structural optimization under $0 \text{ bar}$ allowing cell to change anisotropically.

We note that the lattice constant along $z$ direction was set as about $30$ $Å$ for all models to avoid the interaction with the mirror images.

Advance/NanoLabo enables you to generate such various models on GUI easily.


MoS₂	Ti₂CF₂	Ti₂CO₂

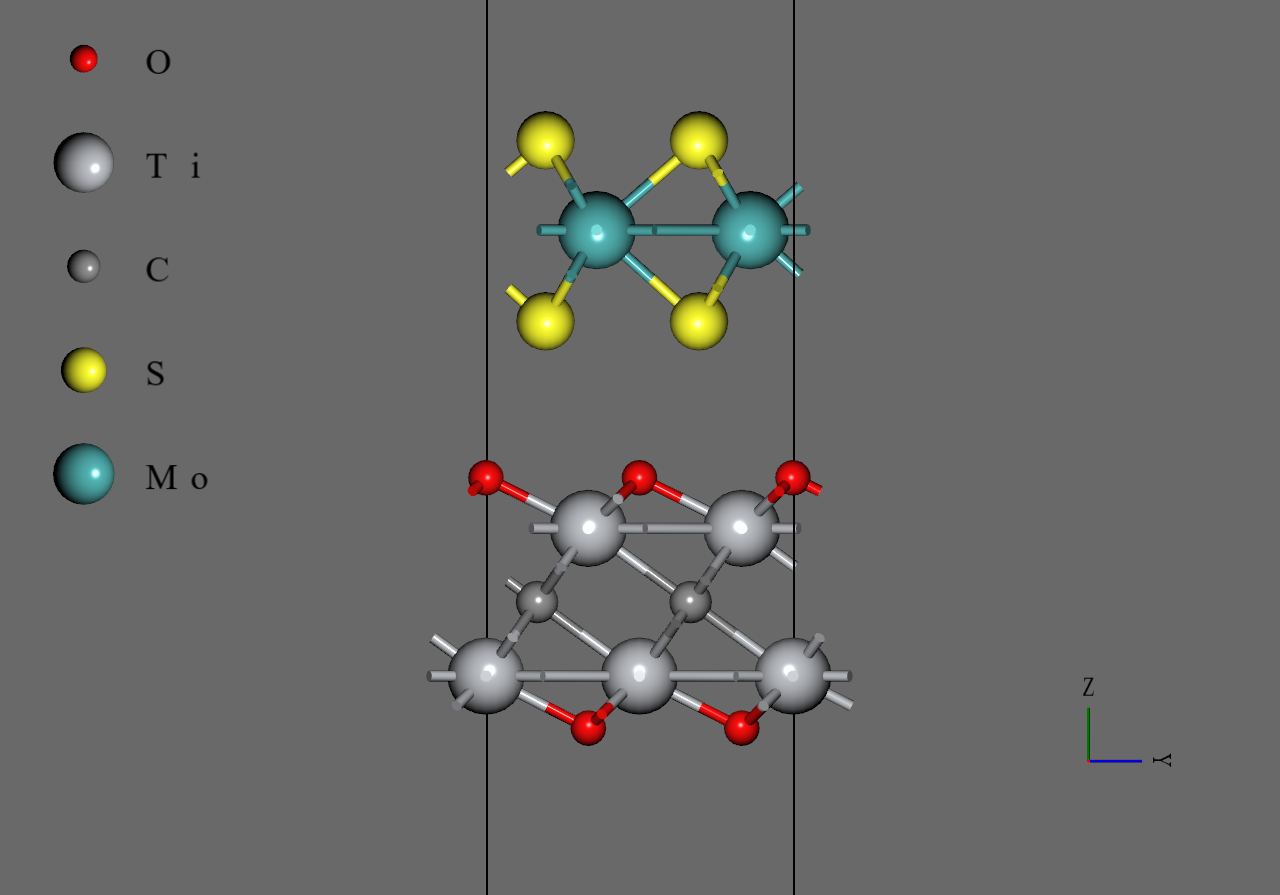
MoS₂/Ti₂CF₂	MoS₂/Ti₂CO₂

Setting of calculation schemes#

We alternated structural optimization and deformation along $x$ direction repeatedly for each model while calculating stress along $x,y$ directions. Note that $x$ directions of the all models correspond to zigzag directions of the honeycomb structures.

We executed the structural optimizations fixing the cell parameters. The strain per deformation step was set as $0.002$ . The structural optimization and deformation were repeated $100$ times.

You can set such a calculation scheme by editing input file directly on Advance/NanoLabo.

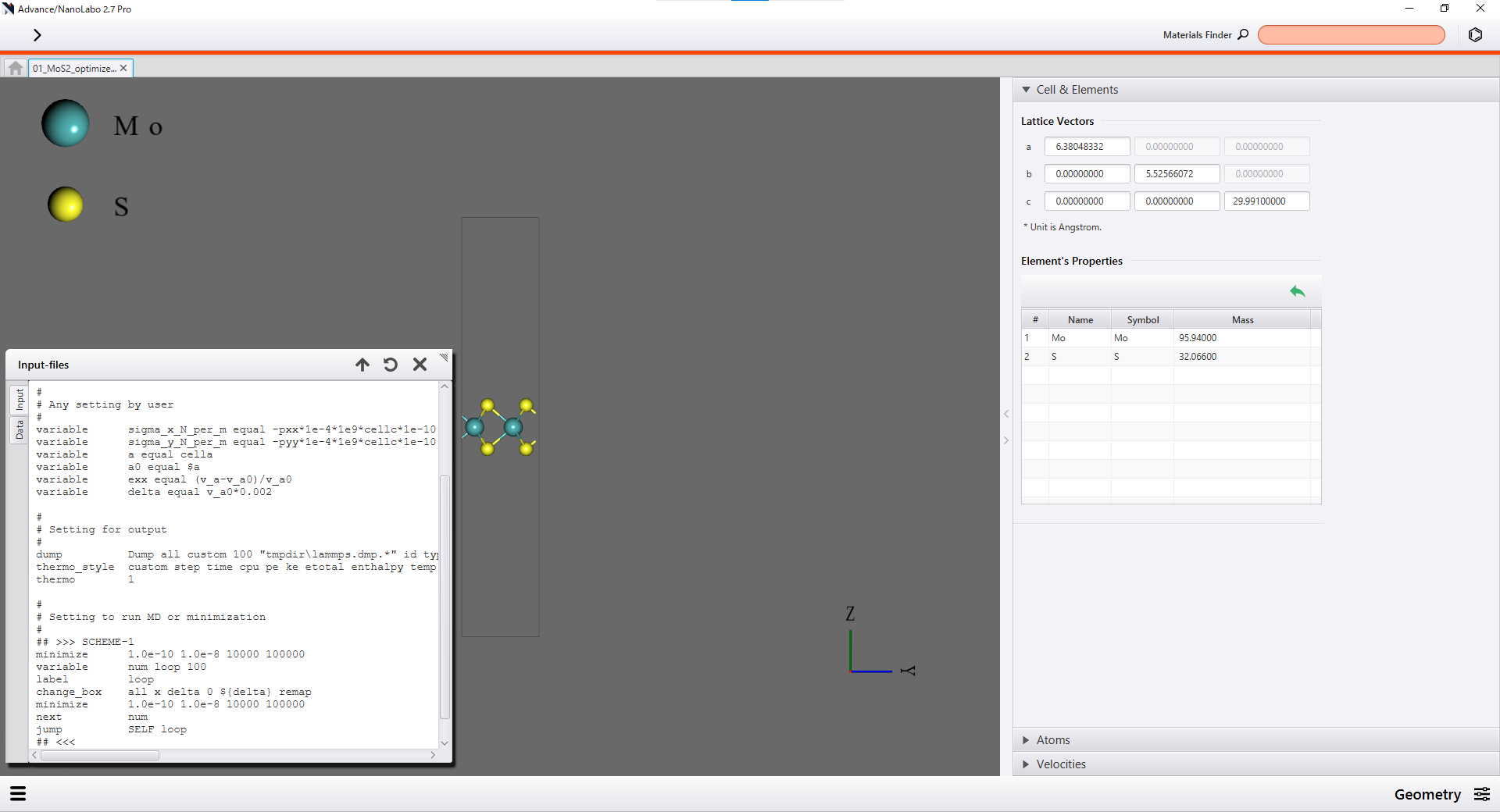
Editing of input file on GUI

Analysis results#

We show the calculated relationships between strain $\epsilon_x$ and stress $\sigma_x,\sigma_y$ for each model below.

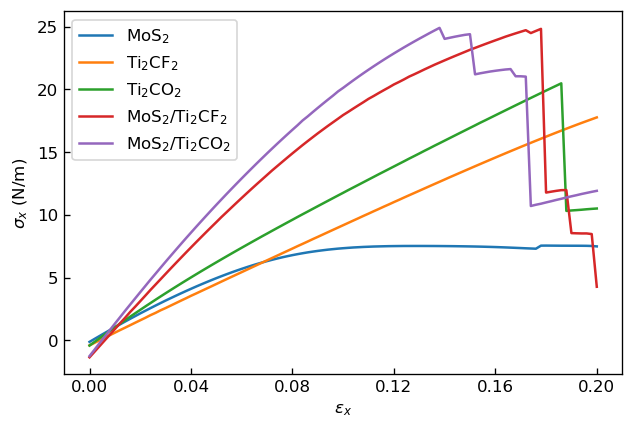
Relationship between strain ε_x and stress σ_x

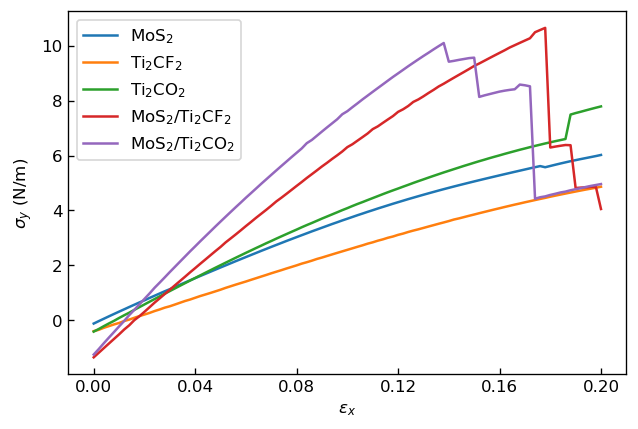
Relationship between strain ε_x and stress σ_y

For two-dimensional systems without shear strain, stress $\sigma$ and strain $\epsilon$ are related as

$\left( \begin{matrix} \sigma_x \\ \sigma_y \end{matrix} \right) = \left( \begin{matrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{matrix} \right) \left( \begin{matrix} \epsilon_x \\ \epsilon_y \end{matrix} \right)$

where $C_{ij}$ $(i,j=1\text{ or }2)$ are elastic constants, and $C_{12}=C_{21}$ due to the symmetry of the elastic constant tensor. Also, the all models are hexagonal systems, so $C_{11}=C_{22}$ ⁸.

Especially, if strain was applied only $x$ direction ( $\epsilon_y=0$ ), stress $\sigma_x$ and $\sigma_y$ are expressed as

$\sigma_x = C_{11}\epsilon_x,$ $\sigma_y = C_{12}\epsilon_x.$

We calculated elastic constants $C_{11}$ , $C_{12}$ by fitting linear functions to the stress-strain curves. The fitted slopes correspond to elastic constants. Note that we fitted the functions to linear regions, where strain is $0$ ~ $0.02$ . We show the plots, in which the horizontal axes correspond to elastic constants calculated via DFT calculation in the previous research³ and the vertical axes correspond to those calculated using M3GNet.

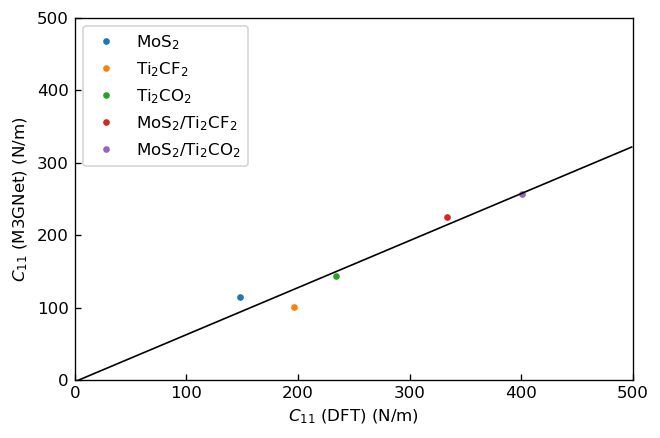
Correlation between C₁₁ calculated by DFT and M3GNet

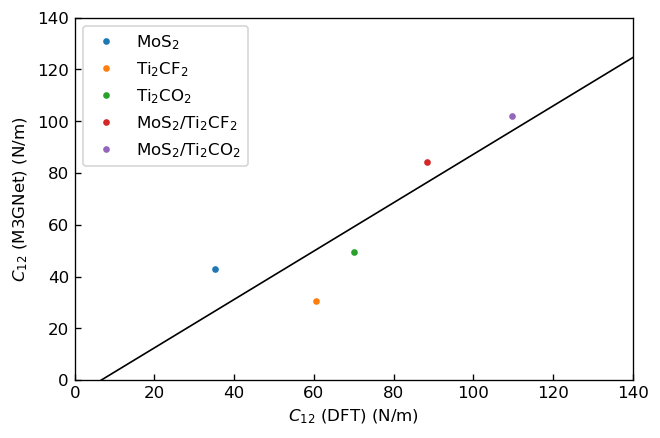
Correlation between C₁₂ calculated by DFT and M3GNet

We fitted linear functions to these plots and show the obtained fitting parameters below.

	Slope	y-intercept
C₁₁	0.65	-2
C₁₂	0.9	-6

We can see that DFT results and M3GNet results have positive correlations for both elastic constants, but M3GNet results tend to be underestimated compared to DFT results.

We also calculated in-plane Young's modulus $E$ and Poisson's ratio $\nu$ of each system from the elastic constants and the following relationship³

$E = (C_{11}^2-C_{12}^2)/C_{11},$ $\nu = C_{12}/C_{11}.$

We show the plots, in which the horizontal axes correspond to Young's modulus $E$ or Poisson's ratio calculated via DFT calculation in the previous research³ and the vertical axes correspond to those calculated using M3GNet.

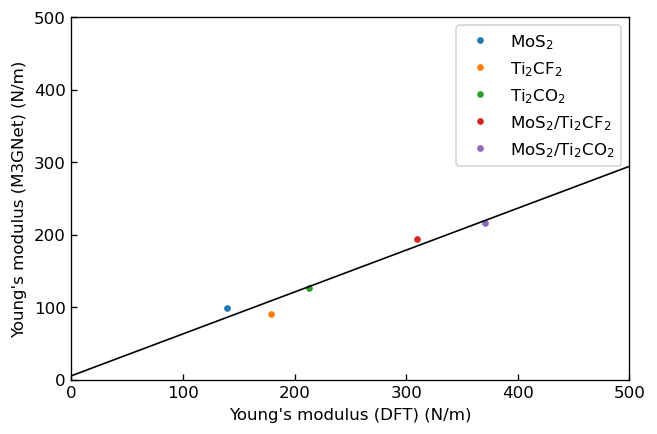
Correlation between Young's modulus calculated by DFT and M3GNet

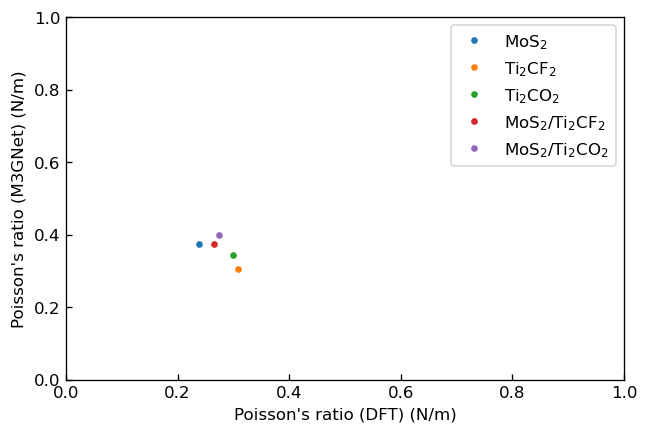
Correlation between Poisson's ratio calculated by DFT and M3GNet

We fitted linear functions to these plots and show the obtained fitting parameters below.

	Slope	y-intercept
E	0.58	5
ν	-0.9	0.6

We can see that the DFT results and the M3GNet results have positive correlations for Young's modulus $E$ , and M3GNet results tend to be underestimated compared to DFT results similarly to the elastic constants. Meanwhile, the DFT results and the M3GNet results of Poisson's ratio $\nu$ don't have positive correlations but have sufficient accuracy to order-estimate Poisson's ratio. Also, the M3GNet results show that formation of heterostructures improves Young's modulus $E$ for each system similarly to DFT results.

The simulation for each system was done about $15$ minutes at longest, which was executed with $20$ thread using OpenMP. It shows that simulation with M3GNet has significantly low computational cost compared to DFT calculation. Also, though M3GNet has been trained on mainly bulk structures, we obtained elastic constants of two-dimensional systems which have positive correlation with DFT results.

Calculation of mechanical properties of MoS2/Ti2CT2 (T=F,O) bilayers using M3GNet#