コンテンツにスキップ

Calculation of anisotropic Young's modulus of single-crystal Ni via molecular dynamics simulation#

We introduce molecular dynamics simulation1 of single-crystal Ni with Advance/NanoLabo, an integrated GUI for nanomaterials.

We calculated stress response to strain applied along different crystal directions and anisotropy of Young's modulus which is used as a measure of stiffness.

Generation of calculation models#

We generated supercell models with (100), (110) and (111) crystallographic orientations from the fcc unit cell model (mp-23) downloaded from Materials Project (we refer to them as Ni(100), Ni(110), Ni(111), respectively).

On Advance/NanoLabo, you can construct such models easily just by specifying Miller index and number of repetitions along each axis.

We show number of atoms and lattice constants of each model in the table below.

System Number of atoms Lattice constant a (Å) Lattice constant b (Å) Lattice constant c (Å)
Ni(100) 4000 35.05798000 35.05798000 35.05798000
Ni(110) 3920 34.70562960 34.70562960 35.05798000
Ni(111) 4032 36.43332154 34.70562955 34.34966497
Ni(100)
Ni(110)
Ni(111)

We adopted embedded-atom-method (EAM) potential as force-field. EAM potential contains many-body terms which originate from embedding atoms in electron density formed by surrounding atoms in addition to two-body terms such as attractive term and repulsive term. EAM potential is mainly used for molecular dynamics simulation of metallic bond systems.

Setting of calculation schemes#

We employed NPT ensemble, in which pressure and temperature are constant, as statistical ensemble. The Nose-Hoover method was used to keep pressure and temperature constant. We set simulation time step as 1 fs.

We equilibrated each system at 300 K and 1 bar for 200000 steps (200 ps). The simulation cells were allowed to deform isotropically during the equilibration.

Then, we deformed each system at constant strain rate of 0.001 Å/ps along <100>, <110>, <111> direction respectively and calculated virial stress for 1000000 steps (1 ns). We kept pressure along the direction perpendicular to loading around 0 bar to calculate uniaxial stress2.

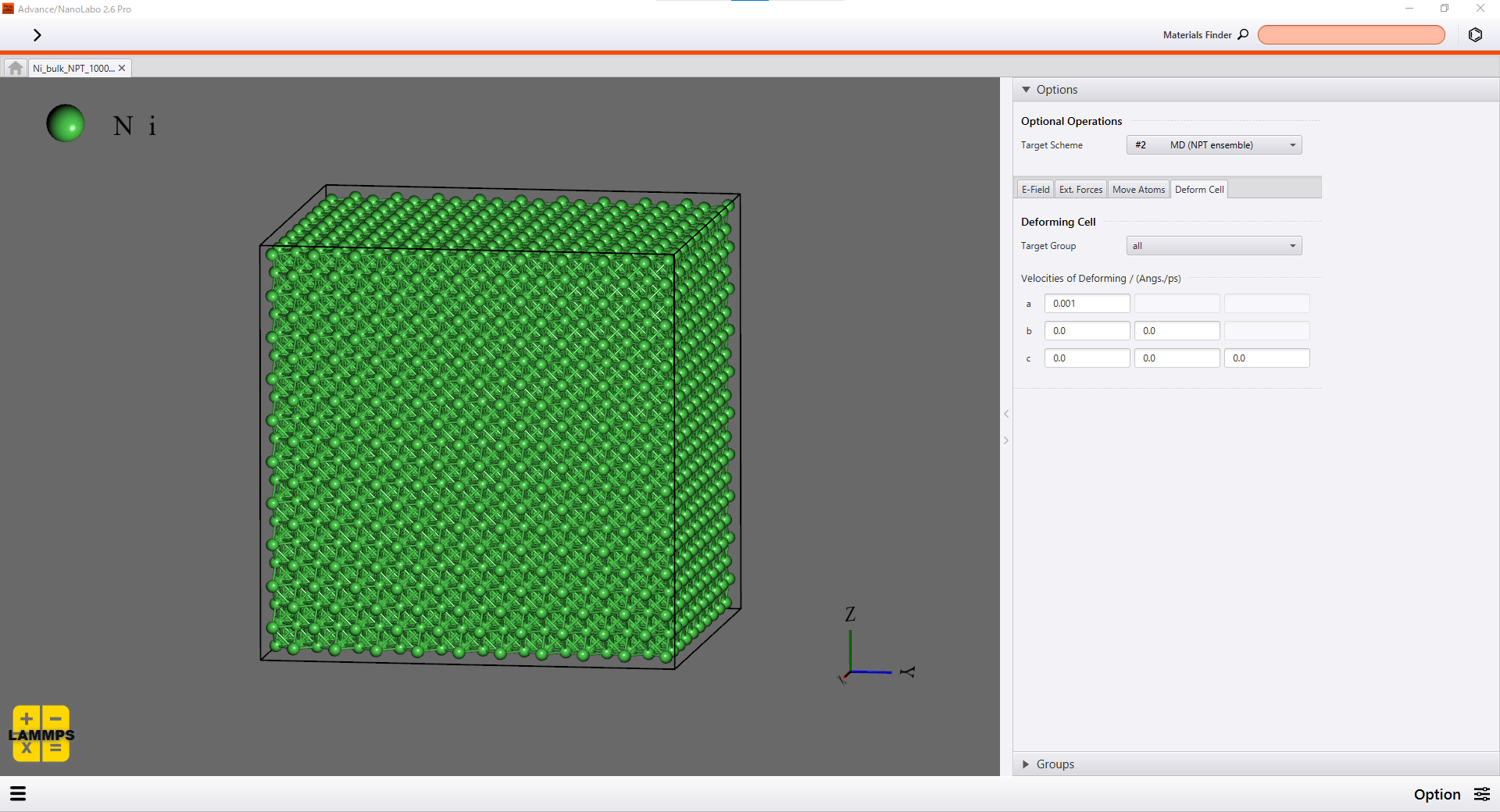
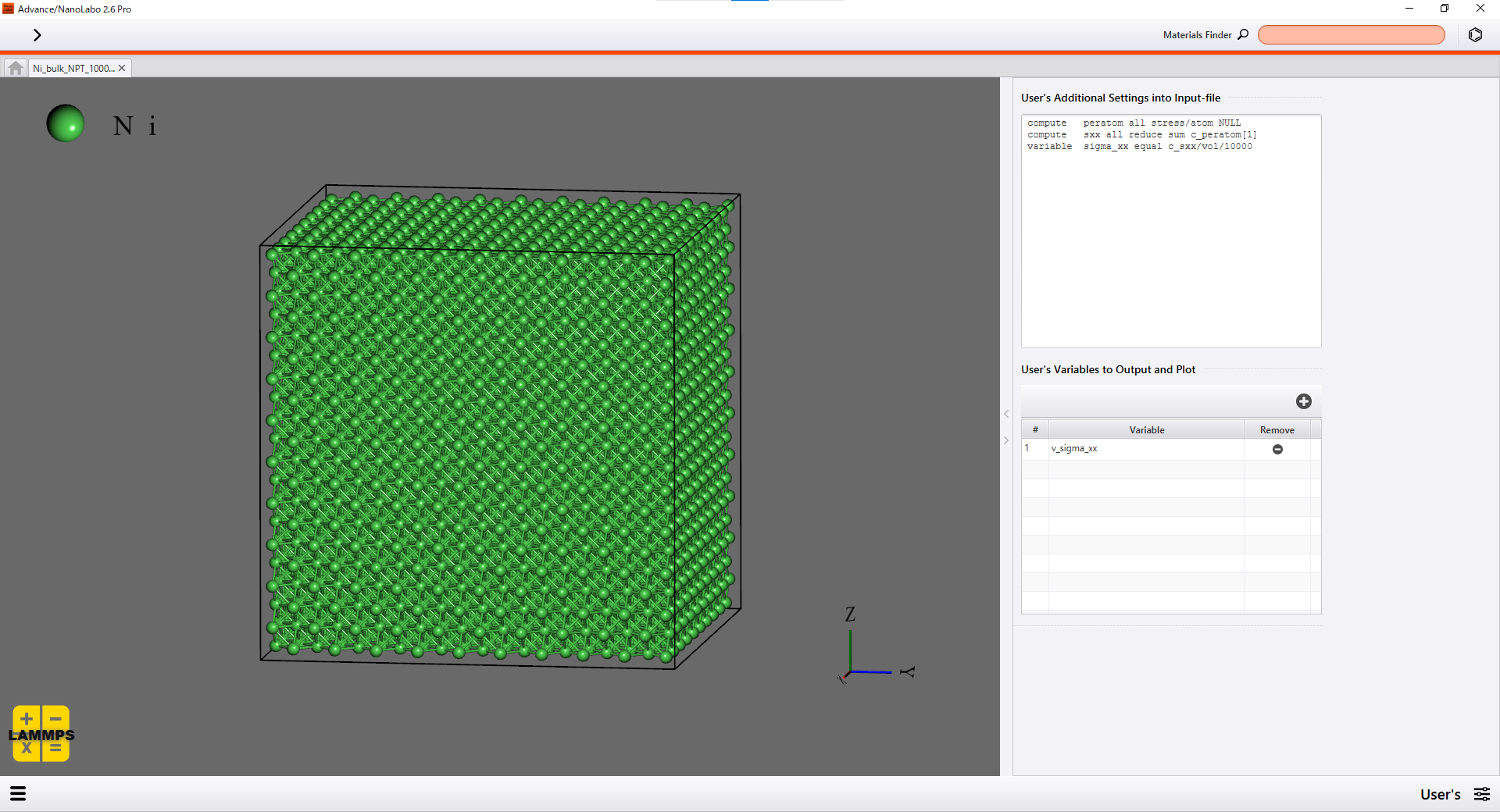
You can set how the simulation cell is deformed on the Option screen of Advance/NanoLabo easily. You can also define any variables to be calculated and visualized on the User's screen. We set calculation of virial stress on the User's screen in this simulation.

Setting on the Option screen
Setting on the User's screen

Tips

You can edit input files directly on the screen displayed before running calculation. We modified the second "fix npt" command of the input file as "fix ensemble all npt temp 300.0 300.0 0.1 y 0 0 1.0 z 0 0 1.0" to keep pressure along y and z direction around 0 bar during loading process3.

Analysis results#

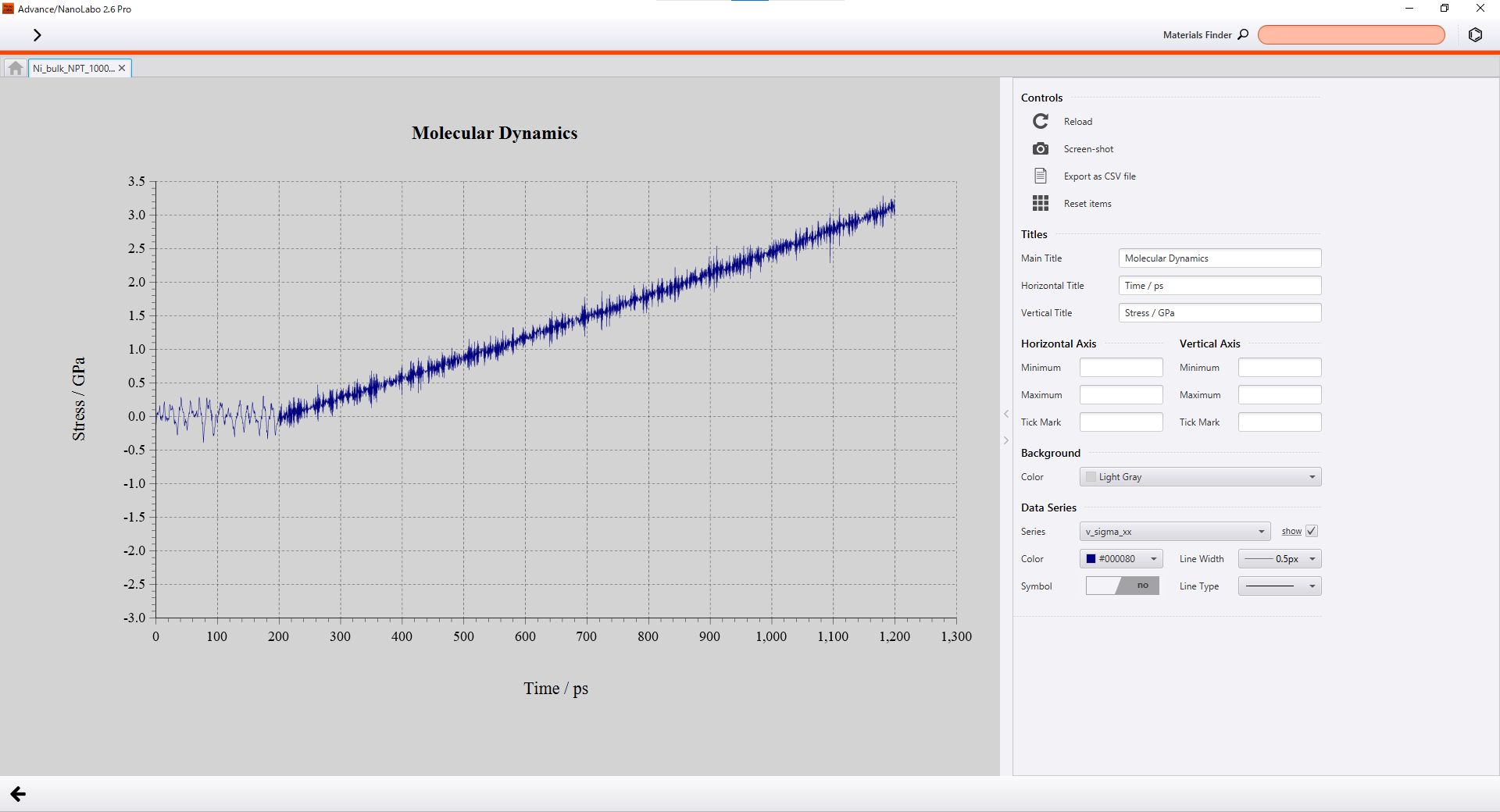
Advance/NanoLabo enables you to visualize calculation results on GUI and export CSV files easily.

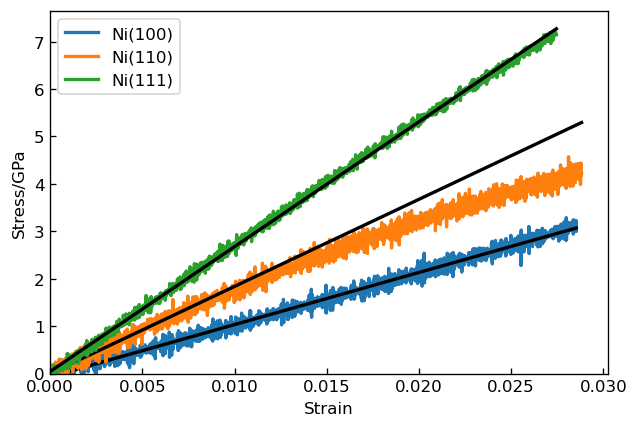
Young's modulus E is defined as the ratio of stress to strain, so we calculated E for each system by fitting linear function to stress-strain relationship4. We show Young's modulus obtained for each system below. The calculated values are comparable with the experimental values for each crystal orientation and reproduce anisotropy of the experimental results.

Visualization on GUI
Calculation of Young's modulus
System
 Young's modulus (GPa) (calculated) Young's modulus (GPa) (experimental)5
Ni(100) 110.0 121.3
Ni(110) 184 203.8
Ni(111) 263.5 262.2

関連ページ#

  1. We used LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) as a solver of molecular dynamics simulation. ↩

  2. MORTAZAVI, Bohayra; AHZI, Saïd. Thermal conductivity and tensile response of defective graphene: A molecular dynamics study. Carbon, 2013, 63: 460-470. ↩

  3. https://docs.lammps.org/fix_nh.html ↩

  4. We used data in the linear region to calculate Young's modulus of Ni(110). ↩

  5. MASUMOTO, Hakaru, et al. Crystal anisotropy and temperature dependence of Young’s modulus in single crystal of nickel. Transactions of the Japan Institute of Metals, 1969, 10.2: 119-123. ↩