ESM法によるK/Cu(001)系の仕事関数の計算#
ESM（Effective Screening Medium）法1は、2次元の周期境界条件を持つ表面（界面）の電子状態計算を精緻かつ効率的に行うための手法です。分極したり電場が印加されたりした表面モデルを正確に扱うことができます。
本事例ではAdvance/NanoLabo上においてESM法を用いたK/Cu(001)系の仕事関数の計算を行いました。
ESM法のセットアップ#
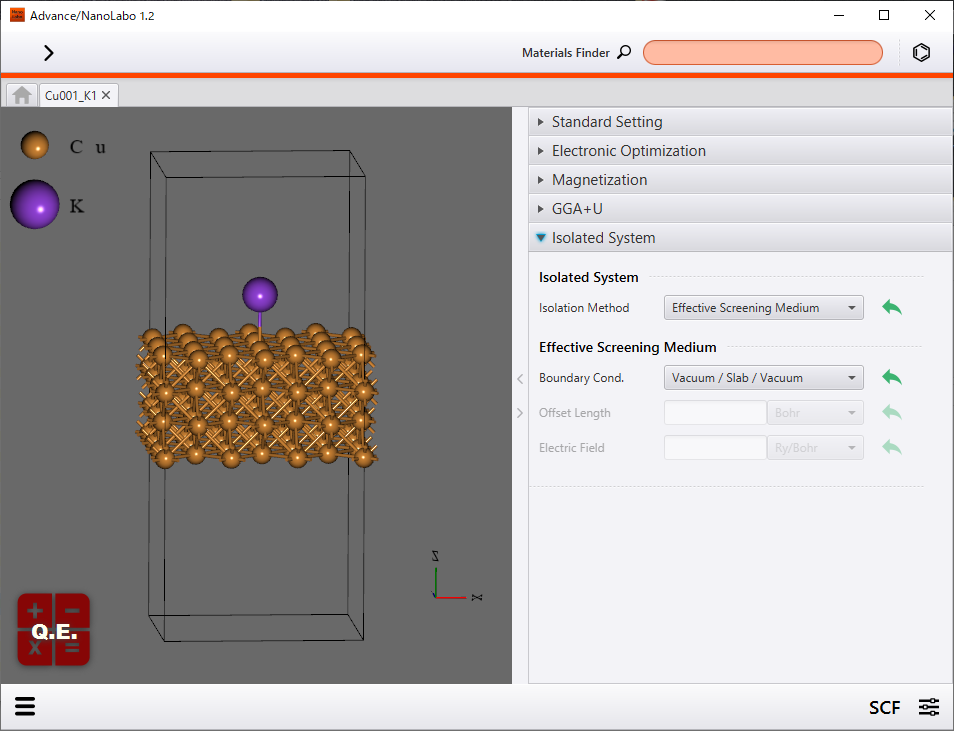
Advance/NanoLaboを用いることで容易にESM法を用いた電子状態計算を行うことができます。必要な設定はESM法を有効化してZ軸方向の境界条件を選択するだけです。ここでは仕事関数の計算を目的としているため、Z軸両端の境界条件には真空を指定しています。
|
|
ESM法の設定
|
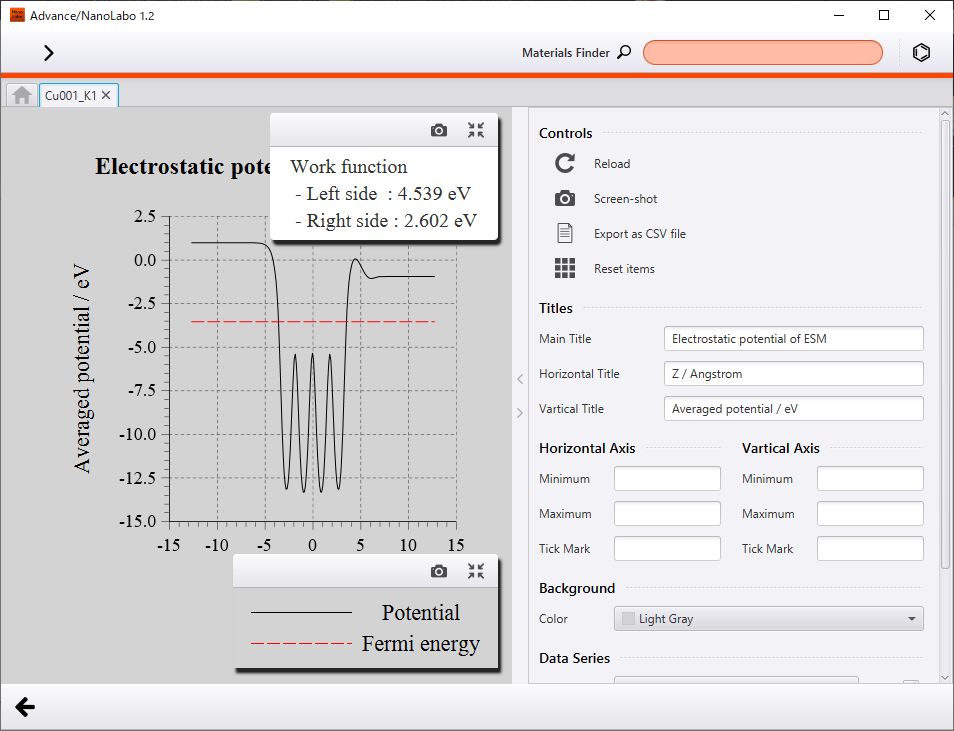
計算結果としてZ軸方向の電荷密度分布と静電ポテンシャル（仕事関数）を示します。
K/Cu(001)系の仕事関数は2.60eVとなりました。Cu(001)表面の仕事関数は4.64eVなので、カリウム原子が吸着することで仕事関数が2eV程度減少することが分かりました。
|
|
電荷密度分布
|
|
|
静電ポテンシャルと仕事関数
|
仕事関数のカリウム被覆率依存性#
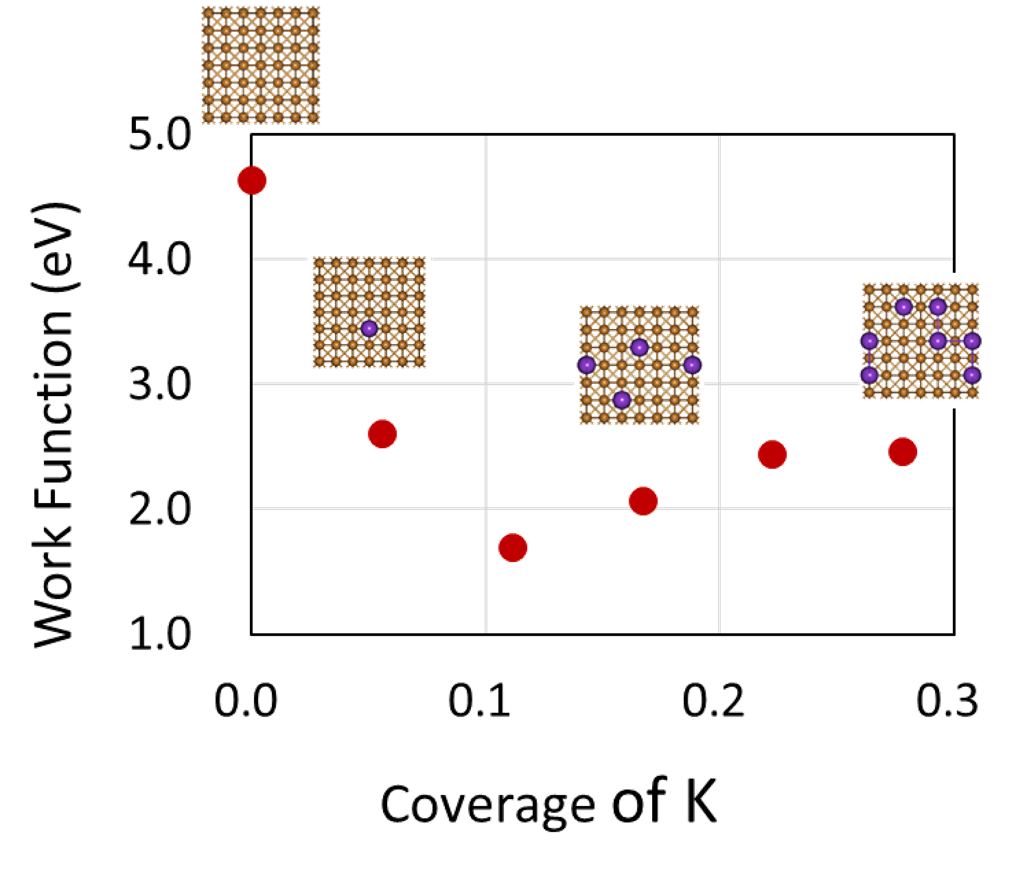
カリウムの被覆率によって仕事関数がどのように変化するかを調べるため、被覆率の異なるK/Cu(001)系について同様の計算を行いました。横軸にカリウムの被覆率2、縦軸に仕事関数をとったグラフを示します。
|
|
仕事関数の被覆率依存性
|
吸着初期においてはカリウムの被覆率が増加するに従い、仕事関数が急激に減少しています。その後、仕事関数は極小点を経て一定値に収束しています。
このような特徴的な仕事関数の被覆率依存性は実験的にも確認されています3。
吸着初期における仕事関数の急激な減少は、カリウム原子がイオン化し表面ダイポールが増加していることに起因するとされています。被覆率がさらに増加すると、カリウム原子が中性化し表面ダイポールの影響が弱まっていると考えられています4。