NEB法によるAlアドアトムの拡散経路の解析#

ナノ材料解析統合GUI Advance/NanoLaboではNudged Elastic Band法（NEB法）を用いて化学反応過程や拡散過程の活性化エネルギーを計算することができます¹。Advance/NanoLabo上で反応過程の始状態と終状態の構造を指定するだけで、容易にNEB計算を行うことができます。

本事例では、NEB法を用いてAl(001)表面上におけるAlアドアトムの拡散過程の解析を行いました。

Note

NEB法による計算機能はAdvance/NanoLabo ver1.2で新たに実装されました。詳細については、ナノ材料解析統合GUI Advance/NanoLaboのページをご覧ください。

NEB法#

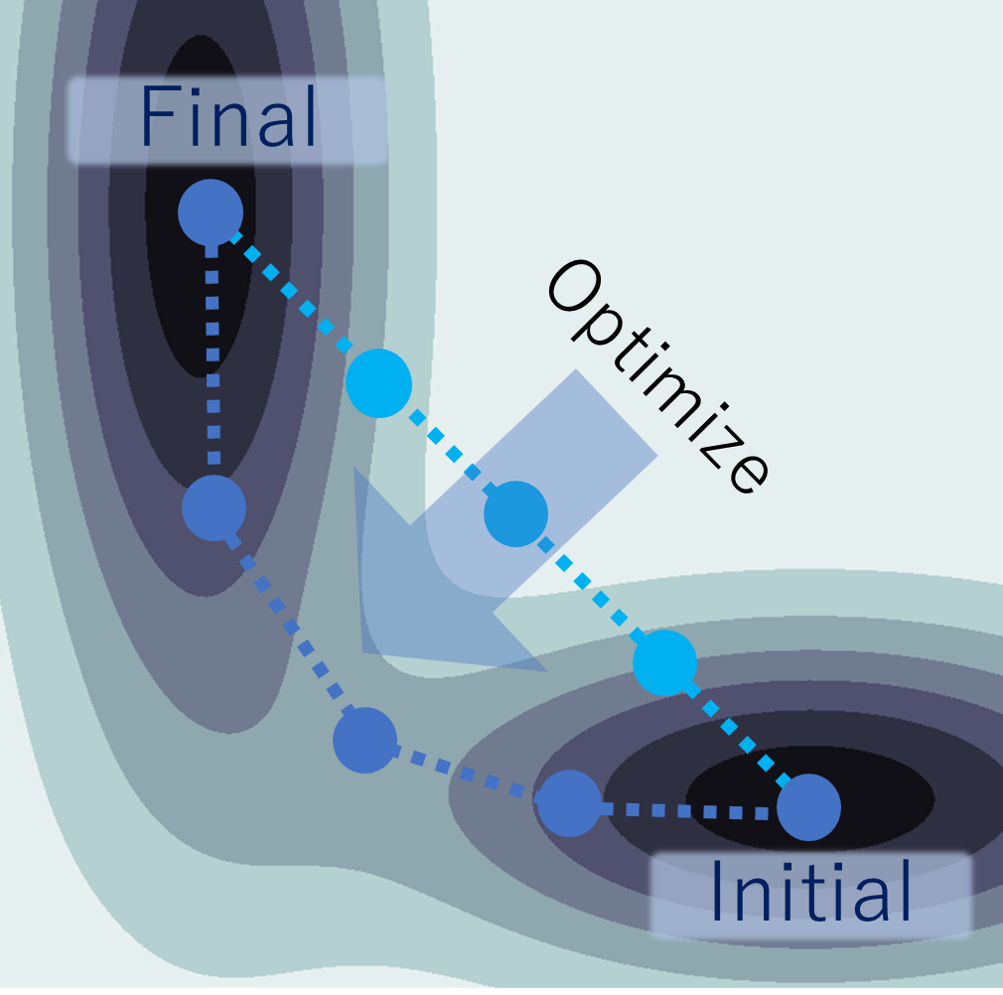
NEB法は始状態と終状態の構造から着目している反応の遷移経路を明らかにする手法です。遷移経路に沿ったエネルギー曲線から反応の活性化エネルギーを求めることができます。例えば表面反応や表面拡散について、最も起こりやすい反応過程を予測したり、実験的に求めた活性化エネルギーと比較したりすることができます。

NEB法のアルゴリズムは次の通りです。始状態と終状態の構造をつなぐ複数の構造（イメージ）を作成します。イメージ間に仮想的なバネを設定して、反応座標に沿った方向にバネ力が働くようにします。この仮想的なバネ力をエネルギー勾配に加えて各イメージを繰り返し構造最適化することで、最終的に反応の遷移経路に沿ったイメージが求まります。

NEB法の概念図

Al(001)表面上でのAlアドアトムの表面拡散#

Al(001)表面上のAlアドアトムの表面拡散について検討します。

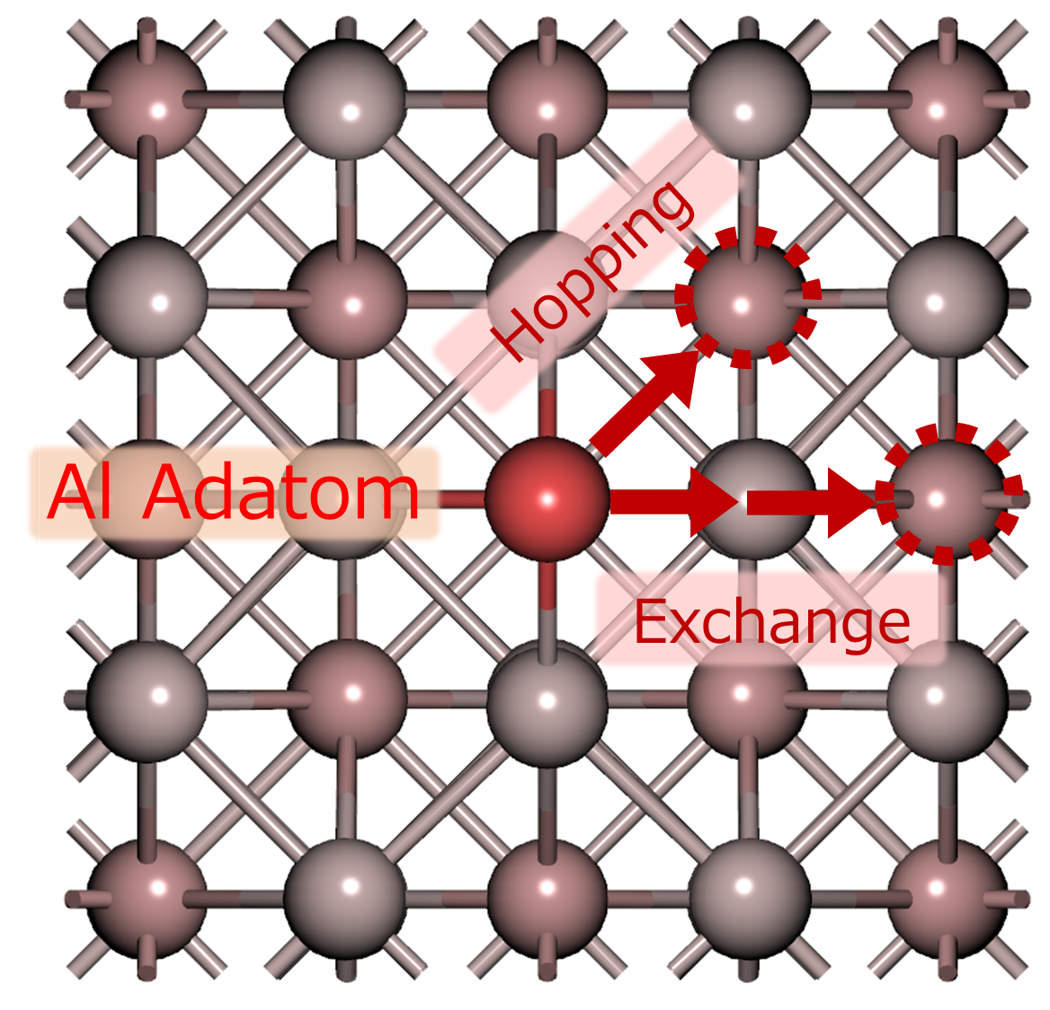
下図のようにアドアトムの拡散経路には2通りの経路が考えられます。1つめは隣接した吸着サイトへと表面上をアドアトムが飛び跳ねる経路（Hopping）です。最も直感的な拡散経路といえます。2つめはアドアトムが1層目の格子内原子と入れ替わることによる拡散（Exchange）です。

本事例ではこの2通りの拡散経路についてNEB法により活性化エネルギーの計算を行い、どちらの経路で拡散がより起こりやすいか予測します。



Hoppingによる拡散	Exchangeによる拡散

NEB計算のセットアップ#

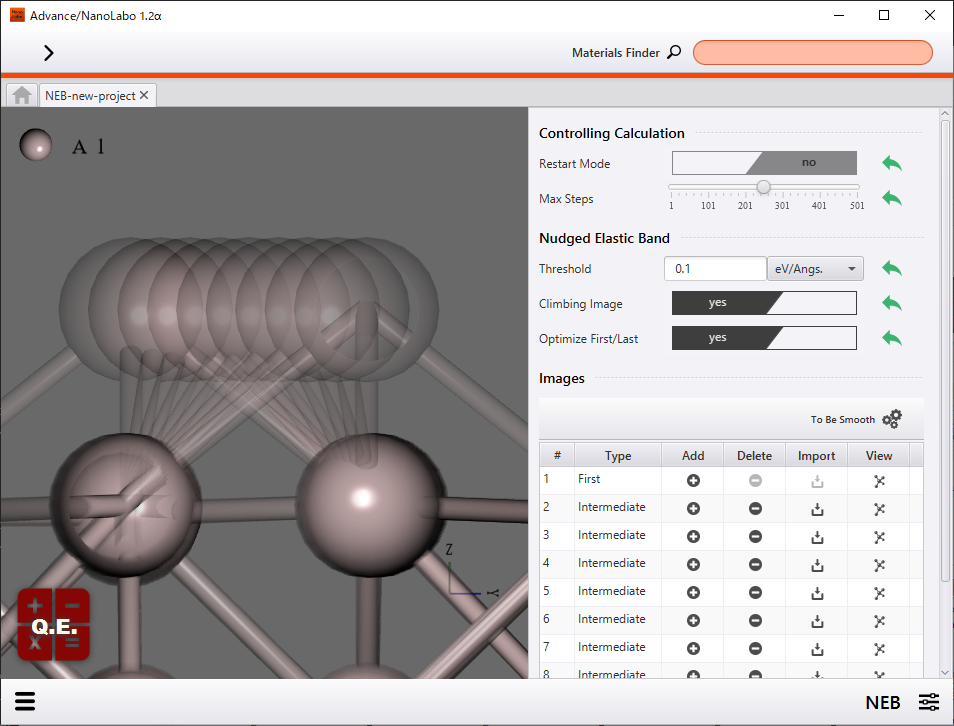
Advance/NanoLaboでは反応の始状態と終状態の構造を指定するだけで、NEB計算の設定を行うことができます。始状態と終状態の構造を指定すると、自動的に構造を補間して複数の初期イメージを生成します。自動で生成された各イメージは残像による可視化機能により、一目で確認することができます。

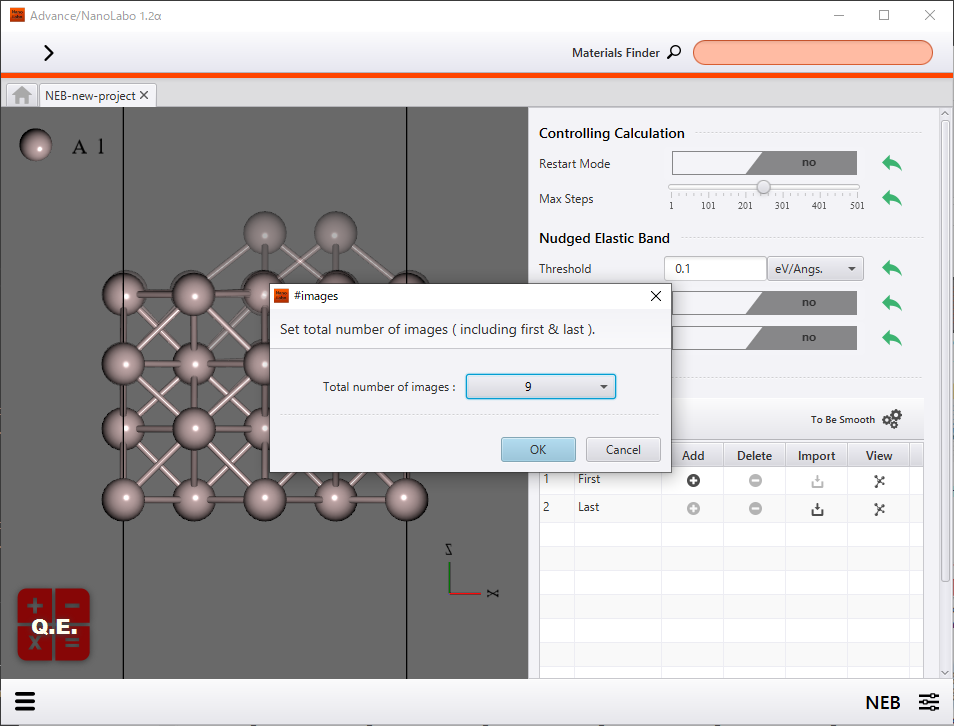
下図はHoppingによる拡散過程についてのNEB計算のセットアップ画面を示しています。本事例では9個のイメージを用いてNEB計算²を行うように設定をしています。


始状態と終状態の構造の設定	残像による各イメージの表示

Hoppingによる拡散過程#

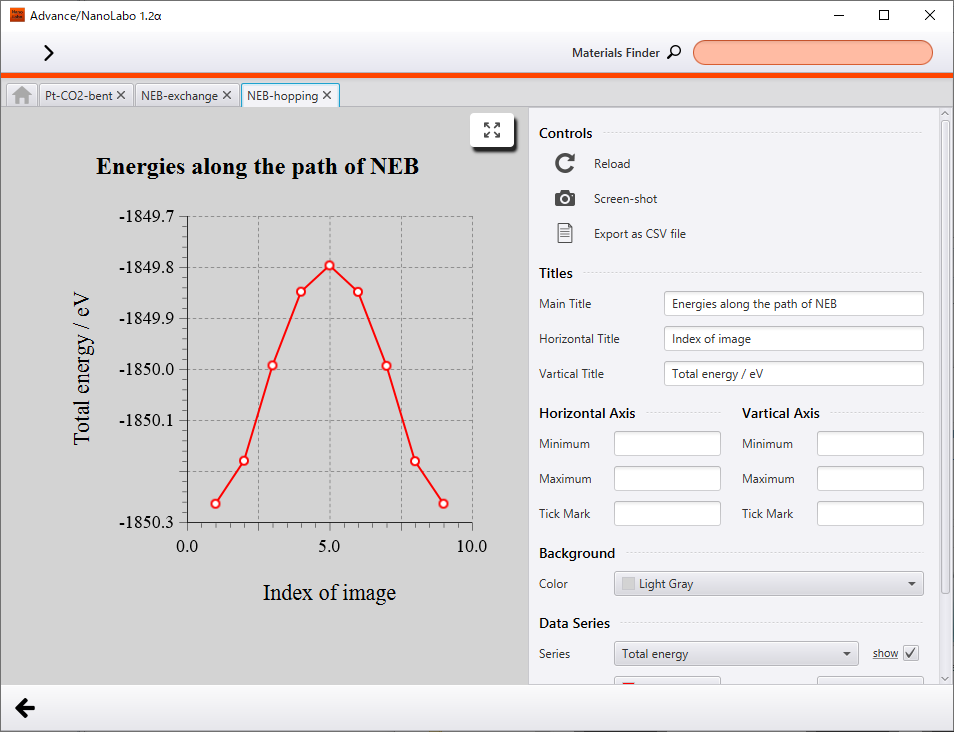
Hoppingによる拡散過程の計算結果を示します。NEB計算により活性化エネルギーは0.46eVとなりました。


エネルギー曲線	各イメージに働く力

Exchangeによる拡散過程#

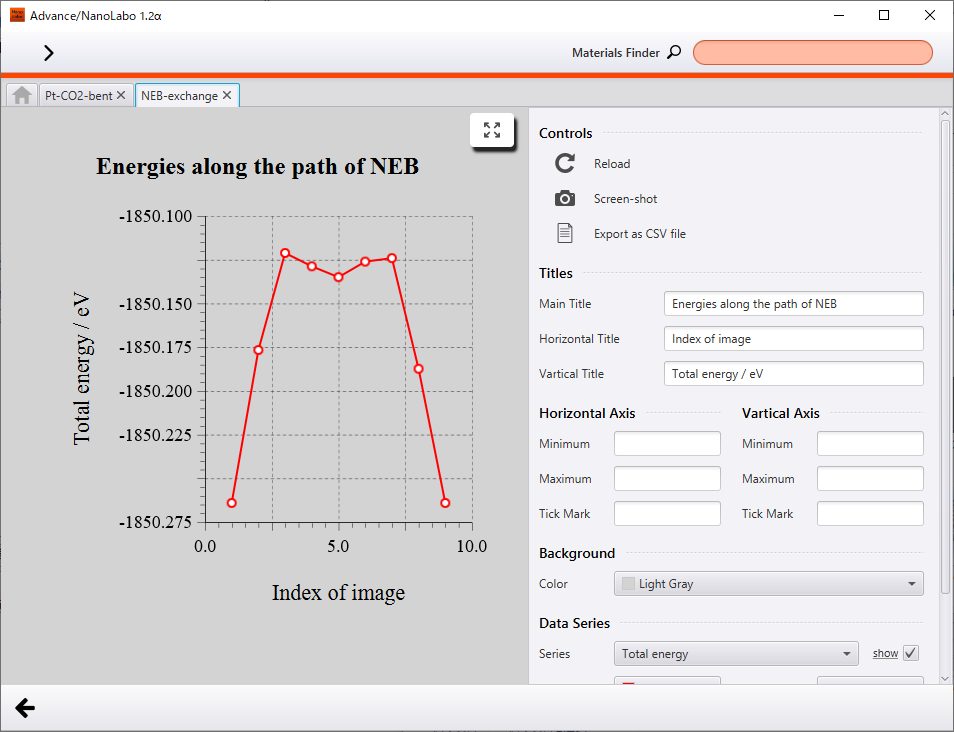
Exchangeによる拡散過程の計算結果を示します。NEB計算により活性化エネルギーは0.14eVとなりました。


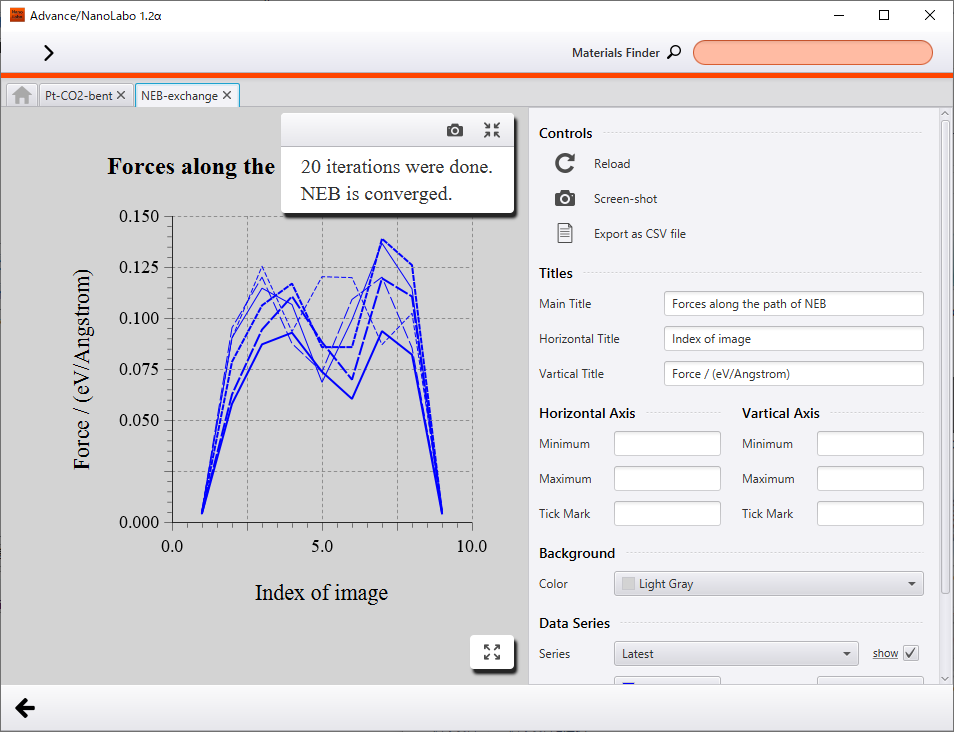
エネルギー曲線	各イメージに働く力

HoppingとExchangeの拡散過程の比較#

拡散経路	活性化エネルギー (eV)
Hopping	0.46
Exchange	0.14

NEB法によりHoppingよりもExchangeによる拡散過程の方が活性化エネルギーが0.3eVだけ低いことが明らかになりました。この計算結果はHoppingよりもExchangeによる拡散過程の方が起こりやすいことを示唆しています。

最も直感的なHoppingの経路よりも、格子内原子との原子の交換を伴うExchangeの経路の方が起こりやすいというのは、一見不思議に思われるかもしれませんが³、この現象は電界イオン顕微鏡（FIM）による実験でも確認されています。

このようなExchangeによるアドアトムの拡散は、Al表面だけでなくPt表面やIr表面など、ほかの金属表面でも観察されています⁴⁵⁶。