コンテンツにスキップ

長大トラス橋の地震応答解析事例#

長大橋梁は重要な社会インフラですが、大規模地震時には、特に震源近傍に存在する橋梁において、その機能が損なわれるほどの損傷を受ける例も多くあります。適切な耐震補強の実施や、被災時の迅速な復旧には、地震動に対して対象となる橋梁がどのような挙動を示すかを知ることが不可欠です。そこで、ここでは長大トラス橋を対象とし、その地震時応答を有限要素法により解析した事例を紹介します。

解析概要#

3 径間連続の長大トラス橋の上部工を梁要素およびシェル要素でモデル化し（図 1 ）、震源近傍の特徴を有する地震波を入力として直接積分法による時刻歴応答解析を行いました。梁要素にはすべて同一の材料定数、断面形状を仮定し、実在する橋梁を参考にその値を設定しました。また、時刻歴応答解析に先立ち固有振動解析を実施し、構造物の動的特性を把握しました。時刻歴応答解析においては、先に得られた 1 次および 3 次の固有振動数において減衰比が 2% となるような Rayleigh 減衰を設定しました。時間積分法は Newmark の β 法（ β=0.25、γ=0.5）を採用し、時間ステップは 0.01 秒、解析時間は 150 秒としました。入力波形は図 2 に示す加速度波形を採用し、実際の計算に際しては加速度波形を適切なフィルタを通して積分することで得た変位波形を強制変位としてモデルの下端に入力しました。1


図 1 : 計算に使用した解析モデル（橋脚は解析対象外）



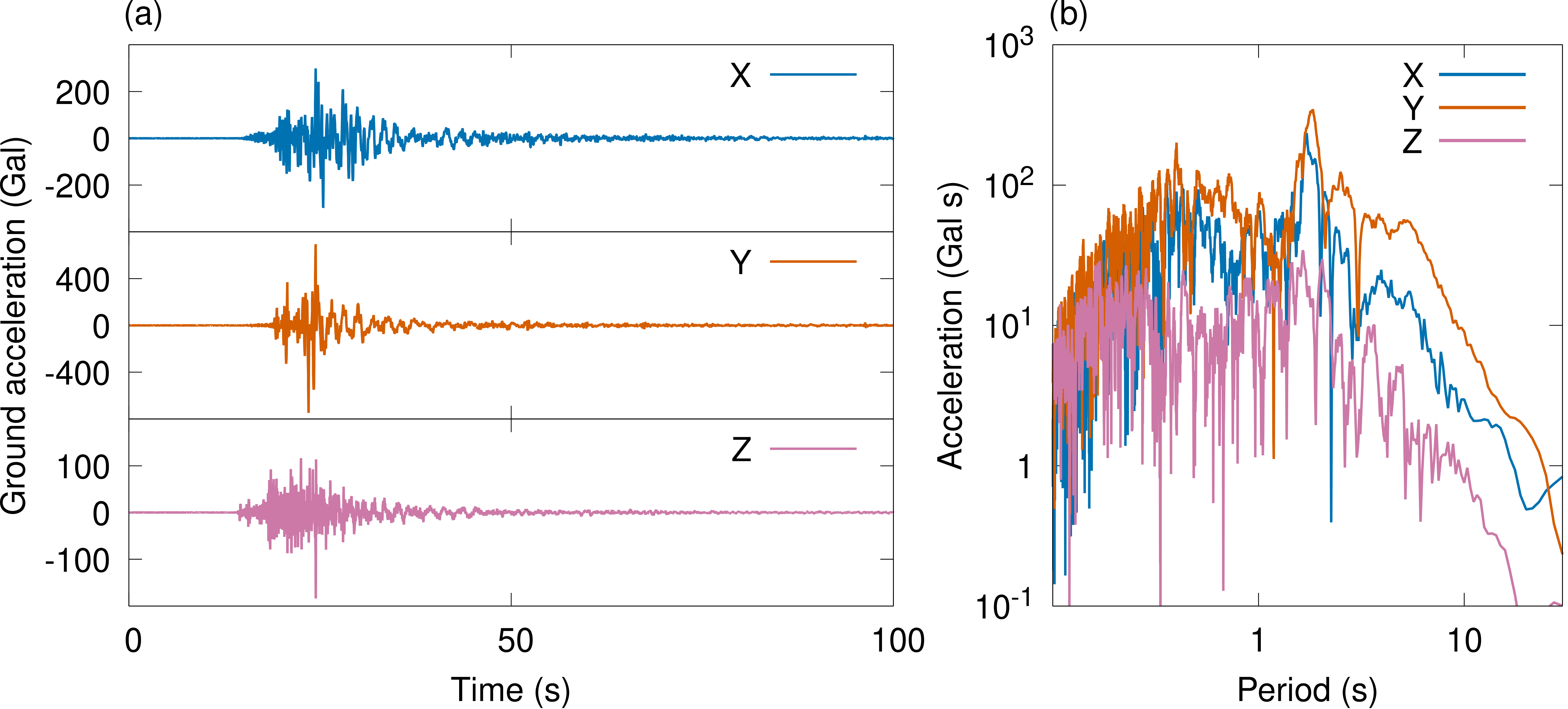
図 2 : 入力として採用した地震動の (a) 加速度波形と (b) その Fourier 振幅スペクトル

解析結果#

  • 得られたモード形状からは、橋軸直角方向に大きく曲がるモードが最も低次のモードとなっており（図 3a ）、次いで鉛直方向のモードとなっていることがわかります（図 3b）。なお、固有振動数は、1 次から順に、0.60, 1.22, 1.61, 2.24 Hz となりました。
  • 図 4 (a) に示す橋梁上端部での相対変位応答および図 4 (b) に示す絶対加速度応答からは、橋軸直角方向の成分が他の成分と比較して極めて大きくなっていることがわかります。これは、入力の地震動の Fourier 振幅スペクトルにおいて、 Y 成分が 1 次モードの固有振動数に近い振動数成分を多く含むことと整合しています。
  • また、入力の地震動では X 成分が Z 成分よりも大きな振幅を有するにもかかわらず、相対変位は X 成分が極めて小さく、 Z 成分のほうが大きくなっています。これは、橋軸方向の振動モードは低次のモードとして表れていないことと符合します。
  • 図 5 に橋軸直角方向の振幅が大きな値をとる t=29.20s におけるスナップショットを示します。変形の形状からは 1 次モードが卓越していることがわかります。また、Mises 応力はスパン中央よりも支承近傍において大きな値となっています。



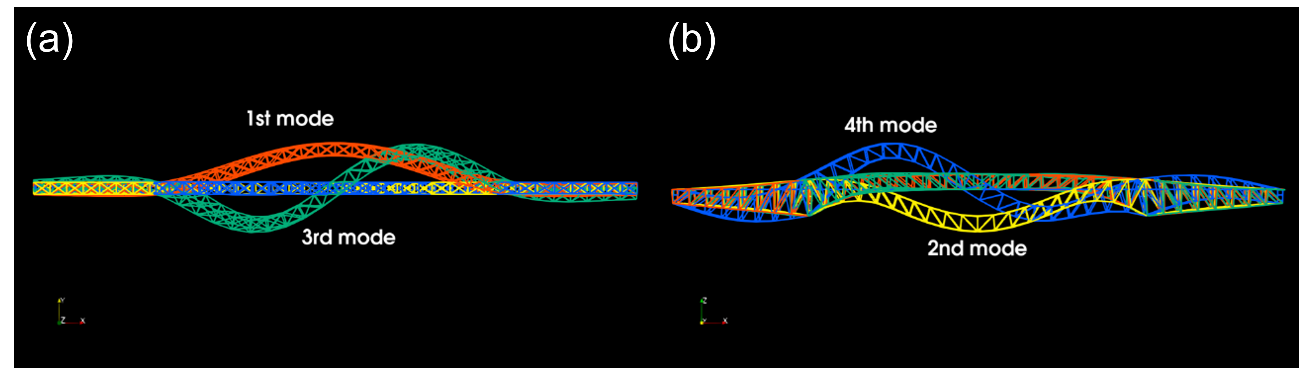
図 3 : 得られたモード形状



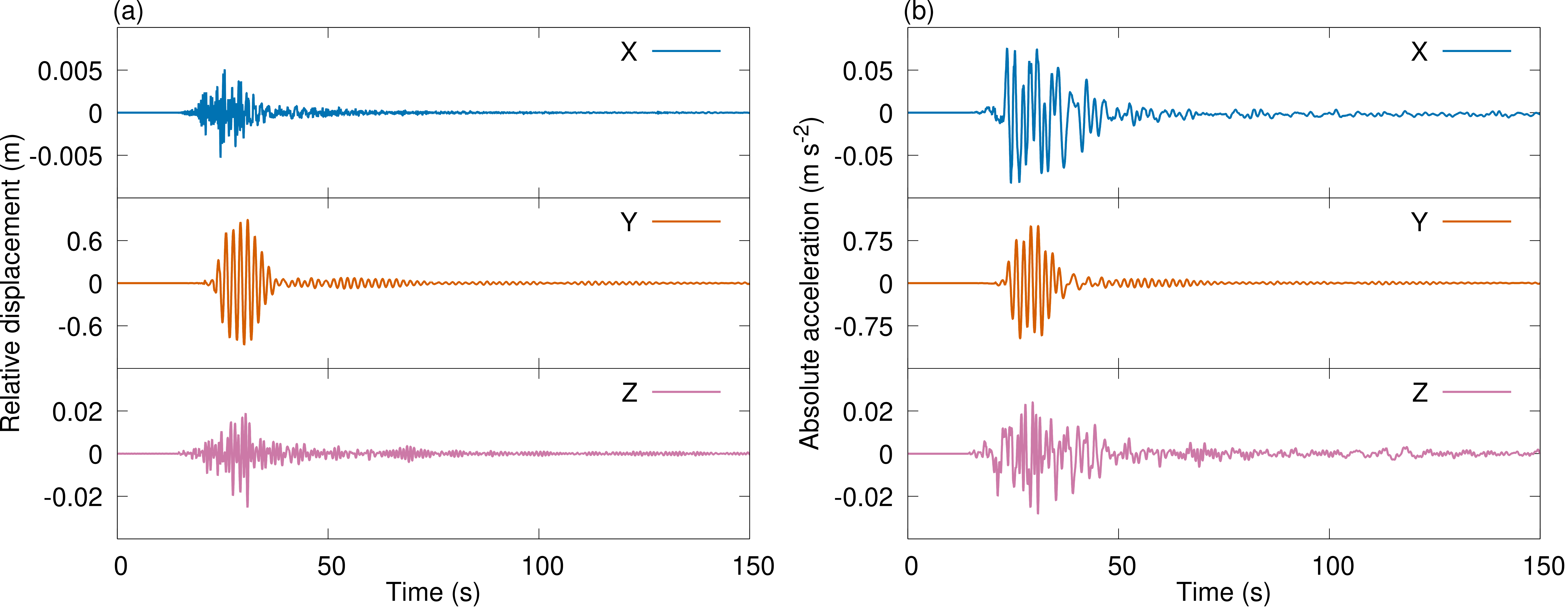
図 4 : 時刻歴応答解析により得られた橋梁上端部での相対変位応答および絶対加速度応答



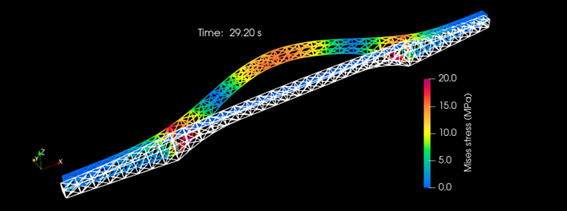
図 5 : 時刻 t=29.20 s におけるスナップショット（変形は 50 倍で描画）

関連ページ#