平行弦ワーレントラス橋の形状最適化#
平行弦ワーレントラス橋の形状を、Advance/FrontSTRの構造解析により形状最適化を行った事例をご紹介します。Pythonの最適化機能を利用します。
最適化の実行方法#
- Advance/FrontSTRによる構造解析を利用した形状最適化
- Pythonスクリプトによる自動化
- 自動化により、数多くの計算実行ファイルをユーザーが用意する必要が無くなります。
- 複雑な解析パラメータの組み合わせは、プログラムが自動で定義してくれます。
- Pythonのscipy.optimizeを使用1
- 準備されたライブラリを使用する事により、自ら最適化のアルゴリズムをコーディングする必要が無くなります。
- 高額な最適化ソフトを準備する必要はありません。
- アルゴリズムの選定やパラメータの定義が重要となります。
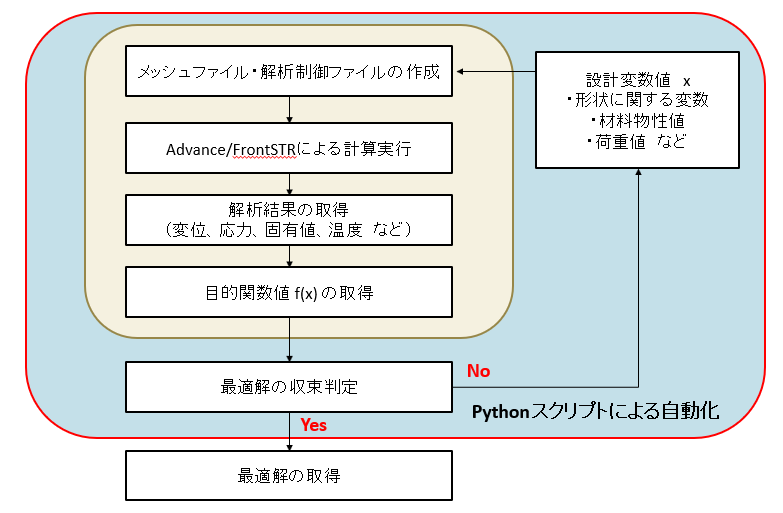
図1 最適化実行スクリプトのフローチャート
解析条件#
平行弦ワーレントラス橋の下弦材に等分布荷重が負荷された際に、橋の質量が最小となる形状を導出します。

図2 解析モデル
既定条件#
- 梁の断面形状:円形
- 境界条件:橋の両端部を完全固定とする
- 荷重条件:下弦全体に等分布荷重を負荷
- 要素タイプ:オイラー梁要素
材料特性#
| 項目 | 値 |
|---|---|
| ヤング率 | |
| ポアソン比 | |
| 許容応力 |
最適化設計条件#
| 項目 | 値 |
|---|---|
| 設計変数 | 高さ H |
| 部材断面の直径 d | |
| 目的関数 | 部材の総質量を最小にする |
| 制約条件 | 部材のミーゼス応力を許容応力以下とする |
| 下弦のたわみ量を0.03m以下とする | |
| 使用した最適化アルゴリズム | 線形近似による制約付き最適化:minimize(method='COBYLA') |
最適化結果(部材を一様断面とした場合)#
| 設計変数 | 制限値 |
|---|---|
| 直径 | 0.001 ≦ d ≦ 1.0 |
| 高さ | 0.1 ≦ H ≦ 2.0 |
*** 初期値(d,H) = (0.001, 0.1)の時 ***
- デフォルトの試行回数(1000回)では収束できず
*** 初期値(d,H) = (0.005, 1.0)の時 ***
- 試行回数:153回 (Advance/FrontSTRによる計算が実行された回数)
- 最適解:(d,H) = (0.0103, 1.296)
ー> 初期値の設定により収束性や所要時間が大きく変わる事もあります
最適化結果(部材毎に異なる断面とした場合)#
下弦材、上弦材、斜材で直径を異なる変数とした場合の計算を実施
| 設計変数 | 制限値 |
|---|---|
| 下弦材の直径 | 0.005 ≦ d1 ≦ 0.02 |
| 上弦材の直径 | 0.005 ≦ d2 ≦ 0.02 |
| 斜材の直径 | 0.005 ≦ d3 ≦ 0.02 |
| 高さ | 0.5 ≦ H ≦ 1.4 |
- 初期値(d1, d2, d3, H) = (0.01, 0.01, 0.01, 1.3)
- 試行回数:52回 (Advance/FrontSTRによる計算が実行された回数)
- 最適解:(d1, d2, d3, H) = (0.0110, 0.0114, 0.0077, 1.330)
ー> 部材の総質量は一様断面のケースの87%に削減されました
最適化結果の応力分布および変形図#
最適化結果におけるミーゼス応力分布と10倍変形図を以下に示します。
最大応力値に変化はありませんが、全体の応力分布に変化が見られるのが確認出来ます。
図3 一様断面
図4 部材ごとに異なる断面
関連ページ#
- 構造解析ソフトウェア Advance/FrontSTR
- 解析分野:構造
- 産業分野:産業機械
- 産業分野:建築土木