無限領域解析の課題を解決する「無限要素」#
有限要素法(FEM)は、複雑な形状や材質を持つ構造物の挙動を正確に予測できるため、現代の構造解析において不可欠なツールです。しかし、FEMには「地盤」のように無限に広がる領域を扱う際に課題がありました。
通常のFEMで無限領域をモデル化しようとすると、要素数が膨大になり計算負荷が跳ね上がります。一方で、計算負荷を抑えるために人工的な境界(モデルの端)を設ければ、本来存在しない境界からの反射波がノイズとなったり、応力結果に拘束の影響が出たりするなど、解析精度を落とす要因となります。
この課題を解決するのが 「無限要素」 です。これは、有限要素モデルの外周に配置することで無限遠方を模擬する特別な要素です。これを用いることで、地盤などの半無限領域を低い計算負荷で、かつ高精度に解析することが可能になります。
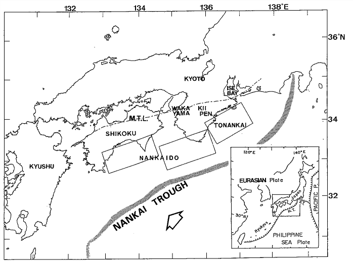
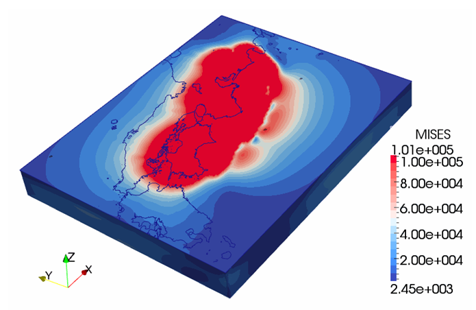
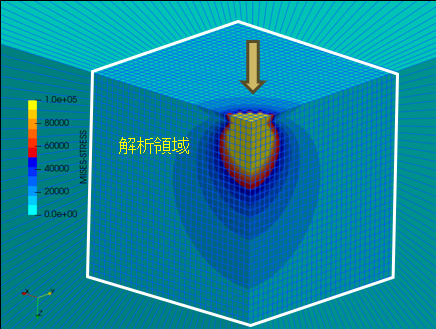
図は、想定地震による地殻変動解析の事例です。解析領域の外側に無限要素を適用しており、地盤振動や大規模構造物との連成解析において、その有効性を発揮しています。
FrontSTRの無限要素#
半無限領域の現象をモデル化するためにFrontSTRが具備する要素を下表に示します。
現在、静解析用に静的無限要素、動解析用には吸収境界要素を使用できます。今回はこれら無限要素の定式化と検証計算例を示します。
| 解析種類 | 要素名 | 要素タイプ | 概要 |
|---|---|---|---|
| 静解析 | 静的無限要素 | 六面体1次 | 標準的な形状関数を使用しますが、自然座標が特定の値に近づくと、要素が無限に漸近します |
| 動解析 | 吸収境界要素 | 三角形1次 四辺形1次 |
境界で波が反射するのを防ぎます。音響や構造の波動伝搬で従来より広く使われています |
静的無限要素#
集中荷重による地盤内応力#
半無限地盤に集中荷重を載荷時の地中応力を解析してブシネスク理論解と比較します。
有限要素だけでは境界の拘束の影響により端部の応力が乱れるが、境界を無限要素とすれば応力の乱れは見られません。
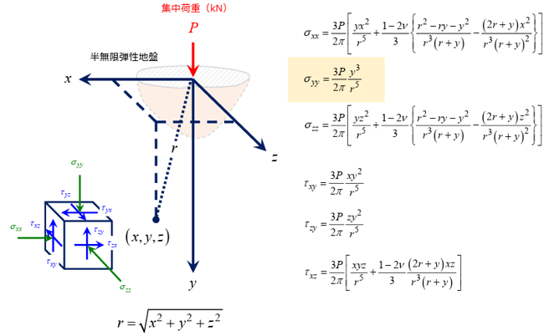
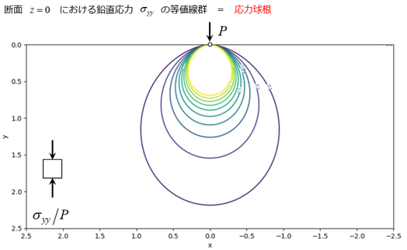
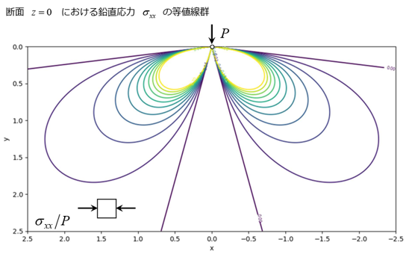
静的無限要素の検証には、ここに示すように無限地盤の1点に集中荷重がかかった場合の地中応力の分布を使いました。
無限要素適用による効果(水平方向応力の比較)#

左の図は水平方向応力分布、右の図は鉛直方向の応力分布です。
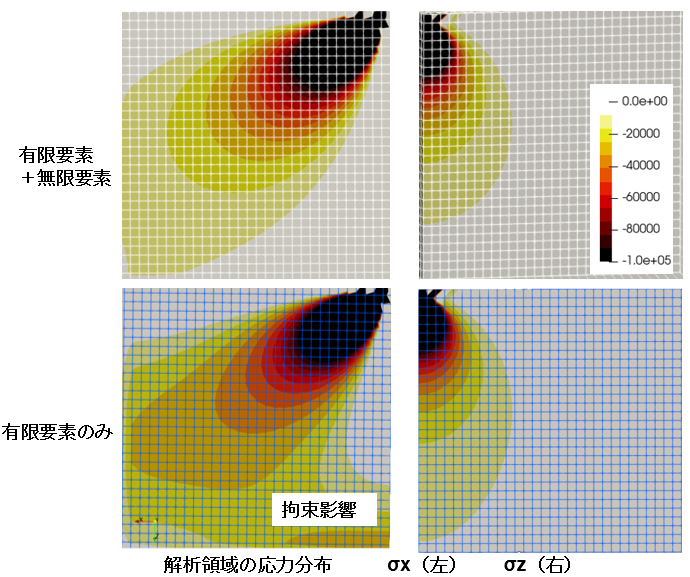
上段に無限要素を用いた応力分布、下段に有限要素のみの応力分布を示します。
無限要素を用いた場合、ブシネスクの理論解と同様な分布となります。
有限要素のみの場合は周囲の拘束の影響を受けて実際にはない応力が発生してしまうことがわかります。
吸収境界要素#
定式化#
吸収境界要素はシンプルな粘性境界です。計算領域の境界に粘性ダンパーを配置することで、波動エネルギーの吸収を模擬します。境界に到達した波動が垂直な方向の速度に比例する抵抗(減衰力)を受けると仮定します。
粘性境界での応力と速度の関係:
ここで、
: 境界に垂直な方向の応力 : 境界に平行な方向のせん断応力
: 媒質の密度
: P波速度 : S波速度
: 境界に垂直な方向の粒子速度 : 境界に平行な方向の粒子速度
この式は、波動が境界に到達すると、その速度に比例した抵抗力が生じ、波動のエネルギーが吸収されることを示しています。
吸収境界の効果#
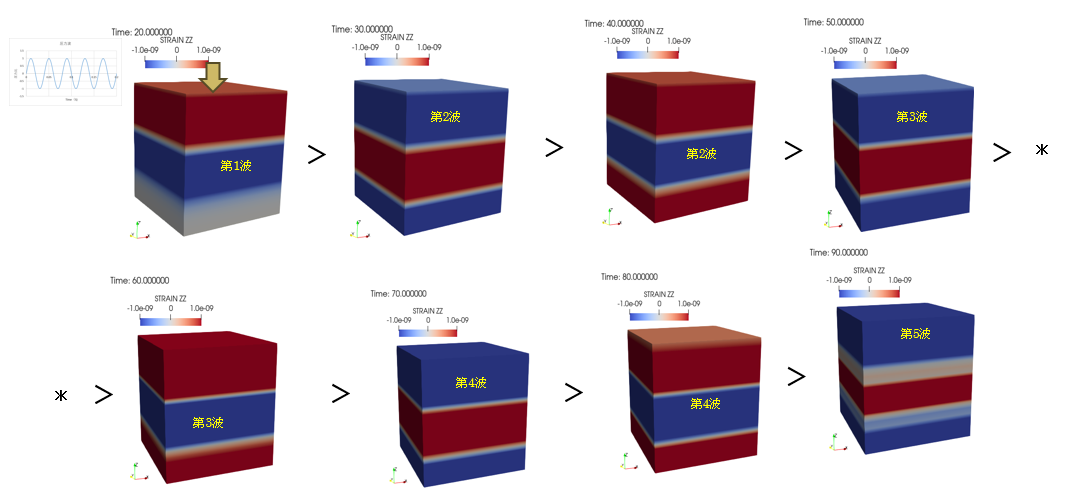
上面から連続的に圧縮波が入射する場合(下面に吸収境界)#
吸収境界に垂直に入射する波の反射波は、ほぼ抑えられます。
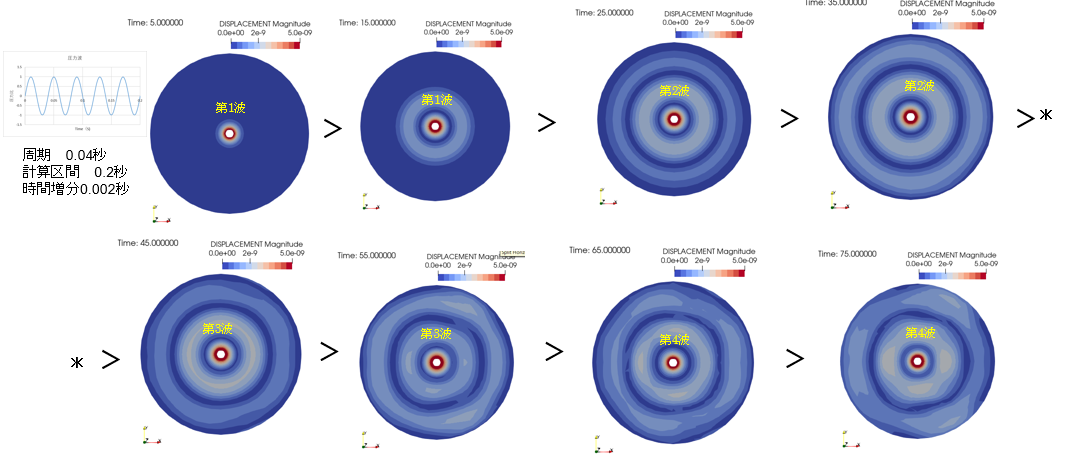
中央から連続的に膨張波が放射される場合(外円周面に吸収境界)#
吸収境界に垂直に入射する波の反射波は、ほぼ抑えられます。